Statystyczna Eksploracja Danych
LABORATORIUM 2
GĘSTOŚĆ ROZKŁADÓW 2D
Głownym zdaniem ćwiczeń będzie dokonanie dyskryminacji za pomocą metod LDA oraz QDA, które zostały w przedstawione na Wykładzie 2. Zostaną do tego wykorzystane dedykowane funkcje z bibliotek MASS oraz klaR, jednak aby w pełni zaznajomić się z tymi metodami warto będzie wyreślić najprostsze hiperpłaszczyzny dyskryminujące "na piechotę". W tym celu należy poznać sposoby wyświetlania poziomic rozkładów 2D za pomocą funkcji contour(), a co za tym idzie również rozpinania siatki na zakresach współrzędnych.
Zaczynamy od uruchomienia dwóch bibliotek: MASS oraz mvtnorm (tę drugą należy zainstalować). Pierwszą już znamy (m.in. funkcje ginv() oraz mvrnorm()), natomiast drugą wykorzystamy do wyznaczania gęstości prawdopodobieństwa wielomwymarowego rozkładu Gaussa (funkcja dmvnorm()).
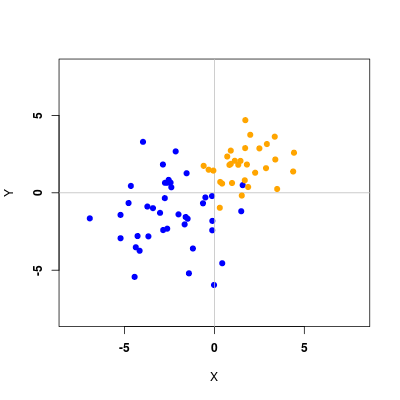
Podobnie jak podczas poprzedniego laboratorium generujemy punkty z dwóch rozkładów Gaussa o zadanych wektorach \(\mathbf{m}_1\) i \(\mathbf{m}_2\) oraz macierzach \(\mathbf{S}_1\) i \(\mathbf{S}_2\)
Następnie wykreślamy punkty
otrzymując efekt podobny do poniższego
Tworzenie dwuwymiarowego rozkładu gęstości prawdopodobieństwa (PDF) jest oczywiście ideowo tożsame z przypadkiem jednowymiarowym: korzystając z odpowiednich funkcji (dnorm() dla 1D oraz dmvnorm() dla 2D), do których przekazujemy parametry rozkładu (\(\mu, \sigma\) dla 1D, \(\mathbf{m},\mathbf{S}\) dla 2D) otrzymujemy gęstość prawdopodobieństwa w danym punkcie. Różnica polega na tym, że w przypadku 2D musimy przekazać do funkcji obie współprzędne \((x_i,y_i)\)każdego punktu \(\mathbf{x}_i\). Rzecz jasna, można po prostu zadeklarować macierz o odpowiednich rozmiarach wypełnioną zerami, a następnie korzystając z dwóch pętli wypełniać ją, jednak takie podejście jest mało "eleganckie". Zamiast tego:
Poniższy kod realizuje te procedury.
Ostatnim punktem jest wykreślenie warstwic rozkładu za pomocą funkcji contour() dla obu klas
otrzymując efekt podobny do poniższego
METODA LDA
Przechodzimy teraz do liniowej analizy dyskryminacji (LDA). Będziemy korzystać z funkcji lda() lecz wcześniej musimy umieścić wszystkie dane w jednej ramce danych, jak również przypisać im przynależność do klas.
Teraz możemy wykonać już funkcję lda() i zapisać efekt jej działania do zmiennej. Sama funkcja opowiada jedynie za proces konstrukcji klasyfikatora, natomiast do przewidywania przynależności dla nowych danych korzystamy z funkcji predict() (funkcja predict() jest podobnie przeciążana jak np. plot() - będziemy korzystać z niej również dla innych klasyfikatorów).
Łatwo można porównać wyniki klasyfikacji za pomocą funkcji table(). W ten sposób tworzymy właśnie macierz pomyłek, musimy jedynie przekazać zarówno oryginalne klasy (ze zmiennej data) jak również jedno z pól zmiennej data.lda.pred (pole class).
Kluczowa informacja, dotycząca przynależności do klas jest zawarta w polu $posterior. Znajdują się tam prawdopodobieństwa a posteriori przynależności do klas dla wszystkich obserwacji. Klasa, dla której prawdopodobieństwo jest największe jest ostatecznie przypisywana do obserwacji i umieszczana w polu $class.
Spróbujmy teraz odtworzyć wartości tych prawdopodobieństw; w przypadku dwóch klas de facto wystarczy nam informacja o \(p(1|\mathbf{x})\), które jest dane wzorem (reguła Bayesa)
Prawdopodobieństwa a priori \(\pi_1\) oraz \(\pi_2\) estymujemy jako liczności klas podzielone przez całkowitą liczbę obserwacji, natomiast gęstości prawdopodobieństwa \(p(\mathbf{x} | 1)\) i \(p(\mathbf{x} | 2)\) są dwuwymiarowymi rozkładami Gaussa o średnich \(\mathbf{m}_1\) i \(\mathbf{m}_2\) estymowanych z danych. Istotną założeniem metody LDA jest to, że macierze kowariancji w obu klasach powinny być takie same. W praktyce uzyskuje się to poprzez uśrednienie wyestymowanych macierzy kowariancji \(\mathbf{S}_1\) i \(\mathbf{S}_2\)
Po tych wszystkich uwagach możemy teraz wyznaczyć wartości prawdopodobieństwa a posteriori przynależności do 1 klasy i porównać je z tymi, które otrzymaliśmy bezpośrednio z funkcji predict()
Suche liczby nigdy nie wytrzymują porównania z wykresem. Biblioteka klaR (do zainstalowania) oferuje funkcję partimat(), za pomocą której można wykreślić rozgraniczenie klas (prostą dyskryminującą). Niestety, ma ona swoje mankamenty i zamiast niej użyjemy funkcji drawparti() (w zasadzie obie powinny dawać to samo), ułatwiając sobie życie za pomocą komendy with().
library(klaR) # Rysowanie prostej rozdzielającej, punktów etc # Dla większej dokładności użyć opcji prec = 200 with(data, drawparti(class, x, y, xlab = "X", ylab = "Y", font = 2))
Na koniec wykorzystamy obliczone przez nas prawdopodobieństwa a posteriori: prosta rozgraniczająca klasy powinna być po prostu warstwicą 0.5 prawdopodobieństwa a posteriori \(p(1|\mathbf{x})\).
# Porównanie z wartościami otrzymanymi z rozkładów contour(xp, yp, matrix(f.lda(gr, me1, me2, Se, pi1, pi2), length(xp)), add = T, levels = 0.5, lwd = 2, lty = 2, col = "blue")
Warto pamiętać, że to samo powinniśmy otrzymać prosto z teorii, przekształcając równanie prostej dyskryminującej
do wygodniejszej postaci
czyli
co skutkuje
potwierdzając, że wszystkie trzy podejścia są tożsame.
METODA QDA
W przypadku kwadratowej analizy dyskryminacji (QDA) korzystamy z funkcji qda(), natomiast dalsze instrukcje są analogiczne do poprzednich
Do wykreślenia granic klas funkcja drawparti() musi zostać wyposażona w opcję method="qda"
# Rysowanie prostej rozdzielającej, punktów etc with(data, drawparti(class, x, y, method = "qda", xlab = "X", ylab = "Y", font = 2))
Aby znów wykorzystać podejście bezpośredniego wyznaczania prawdopodobieństwa a posteriori, należy pamiętać, że w metodzie QDA zakłada się różne macierze kowariancji \(\mathbf{S}_1\) i \(\mathbf{S}_2\), stąd musimy nieco zmodyfikować oryginalną funkcję
NAIWNY BAYES
Warto wspomnieć jaka jest (bardzo istotna!) różnica pomiędzy klasyfikatorem Bayesa, który stanowi podstawę metod LDA i QDA oraz naiwnym klasyfikatorem Bayesowskim. Otóż w tym ostatnim przypadku zakładamy niezależność poszczególnych składowych wektora \(\mathbf{x} = \left(x^1, x^2, ..., x^p \right)^{T}\). W efekcie prowadzi to do następującego wzoru na gęstości prawdopodobieństw \(p(\mathbf{x}|k)\):
Po zainstalowaniu biblioteki e1071 do zestawu powyższych funkcji dochodzi również naiveBayes() realizująca naiwny klasyfikator Bayesowski. Opcja method="naiveBayes" użyta w funkcji drawparti() wykreśli granice klas dla naiwnego klasyfikatora Bayesowskiego.
WIELE KLAS
Nic nie stoi na przeszkodzie, aby powyższe rozważania zastosować do przykładu wielu klas. Poniżej przykładowy kod dla 3 klas
oraz otrzymane rysunki dla metod LDA i QDA