Laboratorium SED - laboratorium 8

Jednym z zadań eksploracji danych jest redukcja wymiaru, czyli określenie, które ze składowych wektora obserwacji są nieistotne lub też jakie inne kombinacje składowych mogą się okazać przydatne do dalszej analizy. Standardową metodą redukcji wymiaru jest analiza składowych głównych (PCA - principal component analysis). Polega ona na znalezieniu nowego kierunku, który maksymalizuje wariancję zrzutowanych na niego obserwacji. Następnie szukamy kolejnego kierunku, również o jak największej wariancji, tyle, że ortogonalnego do poprzedniego etc. Okazuje się, że takie cechy odpowiadają wektorom własnym związanym z kolejnymi wartościami własnymi (począwszy od największej).

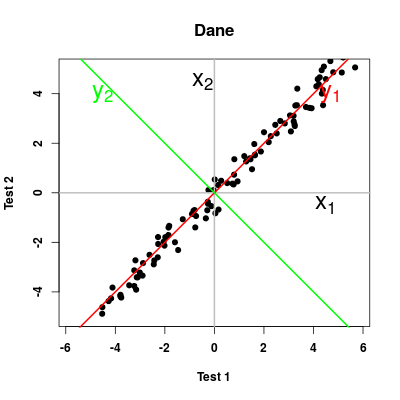
Zaczynamy od przykładu ilustrującego podstawowe cechy PCA dla sztucznie wykreowanych danych postaci $y + \eta = x + \zeta$, gdzie $\eta$ i $\zeta$ są szumem z rozkładu jednorodnego.

# Zależność y = x
x <- seq(-5, 5, by=.1)
y <- x

# Dodanie szumu
eta <- runif(101, 0, 1)
dzeta <- runif(101, 0, 1)

x <- x + eta
y <- y + dzeta

# Wykres
plot(x, y, pch=19, xlab="Test 1", ylab="Test 2", font=2, font.lab=2, xlim=c(-5,5), ylim=c(-5,5), asp = 1)
abline(h=0, v=0, lwd=2, col="gray") abline(0,1,lwd=2,col="red")
abline(0,-1,lwd=2,col="green")
text(4.5,-0.5,expression(x[1]),cex=2)
text(-0.5,4.5,expression(x[2]),cex=2)
text(4.7,4,expression(y[1]),cex=2, col="red")
text(-4.5,4,expression(y[2]),cex=2, col="green") title("Dane", cex.main=1.4)

Otrzymalismy spodziewany wykres, gdzie zależność $y=x$ jest lekko zaburzona ale dalej bardzo wyraźna. Nie uciekając się do generycznej funkji realizującej PCA, sami możemy policzyć skłądowe główne poprzez wyznaczenie wektorów i wartości własnych macierzy kowariancji $\mathbf{S}$ lub macierzy korelacji $\mathbf{Sc}$

# Zapisanie wspolrzednych x i y
# do struktury dataframe

test <- data.frame(x, y)

# Macierz kowariancji
S <- cov(test)

# Macierz korelacji
Sc <- cor(test)

# Wyznaczenie wartości i wektorów własnych
eS <- eigen(S)
eSc <- eigen(Sc)

print(eS)

$values
[1] 17.36473319  0.06932368

$vectors
          [,1]       [,2]
[1,] 0.6961527 -0.7178938
[2,] 0.7178938  0.6961527

print(eSc)

$values
[1] 1.992039893 0.007960107

$vectors
          [,1]       [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068  0.7071068

Teraz wykorzystamy już funkcję princomp() do wykonania PCA. Szczególnie istotne będą jej pola $sdev oraz $loadings - pierwsze pokazuje wartości odchylenia stadardowego związane z poszczególnymi składowymi, a drugie wektory ładunkow PCA. Przeciązona funkcja plot() ilustruje wartości odchylenia

# Wykonanie analizy składowych glownych
test.pc <- princomp(~., cor=T, data=test)

# Wykreślenie wariancji zwiaząnych ze składowymi
plot(test.pc, main="")
title("Wariancja", cex.main=1.4)

print(test.pc$sdev^2)

     Comp.1      Comp.2 
1.992039893 0.007960107

natomiast wykres punktów w nowych współrzędnych dobrze ilustruje faktyczną jednowymiarowość problemu.

# Wykres we współrzędnych składowych głównych
plot(test.pc$scores, xlim=c(-2,2), ylim=c(-2,2), xlab="Składowa 1", ylab="Składowa 2")
title("Składowe", cex.main=1.4)

W wielu przypadkach zwykła analiza składowych głównych nie daje pożądanego rezultatu.

# Dane irysów
data(iris)

# Liniowe PCA
iris.pca <- princomp(~ ., data = iris[,-5], cor = TRUE)
plot(iris.pca$scores, pch = 19, col = as.factor(iris[,5]), xlab

Można wtedy skorzystać z nieliniowej wersji PCA, tj. PCA "wyposażonego" w jądro (kernel) o opowiedniej postaci. Taką opcje oferuje funkcja kpca() z biblioteki kernlab

library(kernlab)

# PCA nieliniowe z jądrem radialnym
iris.kpca <- kpca(~ ., data=iris[,-5], kernel="rbfdot", kpar = list(sigma=0.1))
plot(rotated(iris.kpca), pch = 19, col = as.factor(iris[,5]), xlab = "Składowa 1", ylab = "Składowa 2")

Bardzo ciekawą i prostą w wizualizacji metodą jest skalowanie wielowymiarowe (ang. multidimensional scaling - MDS). W ogólnym ujęciu, za pomocą tego podejścia (funkcja cmdscale())możliwe jest przedstawienie odległości pomiędzy poszczególnymi punktami (obserwacjami) w niskowymiarowej (np 2D) przestrzeni. Jest to szczególnie proste w przypadku danych geograficznych, dla których posiadamy macierz wzajemnych odległości:

# MDS dla miast Europy
euro.cmd = cmdscale(eurodist, k = 2)

# Tworzenie rysunku
plot(euro.cmd[,1], euro.cmd[,2], type = "n", xlab = "", ylab = "", axes = FALSE, main = "MDS Europa")
text(euro.cmd[,1], euro.cmd[,2], labels(eurodist), cex = 0.9, xpd = TRUE)

Warto jednak zwrócić uwagę na fakt, że funkcja dist() umożliwia nam wyznaczenie odległości pomiędzy zupełnie innymi typami danych (tzn. nie odegłości geograficznych), a co za tym idzie, po przekazaniu do funkcji cmdscale() również wizualizację takiegu układu.

# Dane dotyczące głosowań na prezydenta w stanach USA
votes.repub <- cluster::votes.repub

# Pozbywamy się wartości NA
dates <- c(1:15)
ind <- apply(is.na(votes.repub[,-dates]), 1, any)
votes <- votes.repub[!ind, -dates]

votes.cmd <- cmdscale(dist(votes))

plot(votes.cmd, type = "n", xlab = "", ylab = "", axes = FALSE, main = "Stany USA w wyborach prezydenckich")
text(votes.cmd, labels = rownames(votes.cmd), cex = 0.9, xpd = TRUE)