Statystyczna Eksploracja Danych
LABORATORIUM 1
DYSKRYMINACJA FISHEROWSKA
Teoria związana z tym zdaniem jest dostępna m.in. na stronie wykładu Statystyczna Eksploracja Danych: Wykład 1 (dyskryminacja Fishera dla dwóch klas) oraz Wykładem 2 (dyskryminacja Fishera dla wielu klas).
Pierwszym zadaniem, związanym z dyskryminacją Fishera jest znalezienie kierunku (wektora) \(\mathbf{a}\), który optymalnie rozdziela zrzutowane na niego obserwacje.
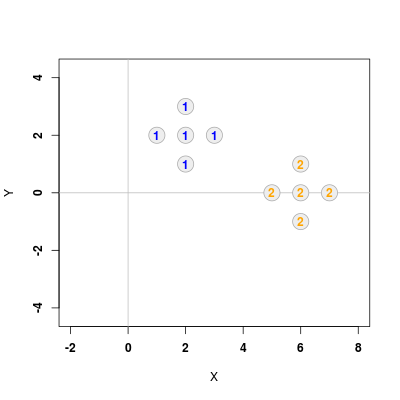
Załóżmy, że chcemy dokonać dyskryminacji zbiorów przedstawionych na poniższym rysunku (Rys. 1.1)
Zaczynamy od uruchomienia biblioteki MASS, która będzie potrzebna do niektórych funkcji, takich jak ginv() (odwracanie macierzy) czy mvrnorm() (losowanie wartości z wielowymiarowego rozkładu Gaussa).
Następnie tworzymy dwie ramki danych X1 oraz X2, w których umieszczone zostają współrzędne obserwacji należących do poszczególnych klas (odpowiednio "niebieskiej" i "pomarańczowej"). Kolejnym krokiem jest wyznaczenia wartości średnich m1, m2 oraz macierzy kowariancji S1, S2.
Zgodnie z Wykładem 1 wektor \(\mathbf{a}\) otrzymujemy dokonując maksymalizacji wyrażenia
gdzie \(\mathbf{W}\) (macierz zmienności wewnątrzgrupowej) jest zdefiniowana jako
a \(n_1\) i \(n_2\) to liczby obserwacji w odpowiednich klasach, natomiast \(n\) jest ich całkowitą sumą (\(n=n_1+n_2\)). Maksymalizacja \(J\) prowadzi do następującego wyrażenia na wektor \(\mathbf{a}\)
Korzystając z tych informacji łatwo znajdujemy odpowiednie wartości, używając funkcji ginv() do odwrócenia macierzy oraz operatora %*% do wykonania mnożenia wektorowego jak również funkcji nrow(), zliczającej rzędy w ramce danych:
# Liczba elementów klas 1 i 2 oraz całkowita liczba n1 <- nrow(X1) n2 <- nrow(X2) n <- n1 + n2 # Wyznaczenie macierzy zmienności wewnątrzgrupowej W W <- ((n1 - 1) * S1 + (n2 - 1) * S2)/(n - 2) # Wyznaczenie wektora a a <- ginv(W) %*% (m2 - m1)
Aby przedstawić punkty 1 klasy, skorzystamy z funkcji plot() z parametrem asp = 1, co zapewni właściwe proporcje obrazu. Następnie użyjemy funkcji points(), aby dodać elementy klasy 2. Na końcu na punkty nałożymy numery klas (funkcja text()).
# Nanoszenie punktow na wykres plot(X1, xlim = c(-2,7), ylim = c(-2,4), pch = 21, col = "#AAAAAA", bg = "#EEEEEE", cex = 3, xlab = "X", ylab = "Y", font = 2, asp = 1) abline(v = 0, h = 0, col = "gray") points(X2, pch = 21, col = "#AAAAAA", cex = 3, bg = "#EEEEEE") text(X1, "1", col = "blue", font = 2) text(X2, "2", col = "orange", font = 2)
Rzecz jasna, sam wektor \(\mathbf{a} = (a_x, a_y)^{T}\) wskazuje jedynie optymalny kierunek, natomiast nam zależy na wykreśleniu prostej. W tym celu skorzystamy z funkcji abline(B, A), której argumentami są współczynniki relacji liniowej \(Y = A X + B\). W naszym przypadku \(A = a_y / a_x\) oraz \(B = 0\). Pozostaje kwestia wyznaczenia płaszczyzny dyskryminującej danej spełniającej zależność
którą w rozpatrywanym przypadku można przedstawić w trochę "łatwiejszy" sposób jako
Finalnie
# Rysowanie prostych rozdzielajacych b <- 0.5 * t(a) %*% (m1 + m2) abline(0, a[2] / a[1], col = "red", lty = 2) abline(b / a[2], -a[1] / a[2], col = "red", lwd = 2)
co daje poniższy rezultat
Korzystnie jest sprawdzić działanie dyskryminacji Fisherowskiej dla większe liczby danych. W tym celu wykorzystamy funkcje do losowania wartości z wielowymiarowego rozkładu Gaussa
S <- matrix(c(1,0,0,1),2,2) mt1 <- c(2,2) mt2 <- c(6,0) n1 <- 60 n2 <- 60 n <- n1 + n2 X1 <- mvrnorm(n1, mt1, S) X2 <- mvrnorm(n2, mt2, S)
Warto zmienić styl rysowania punktów, żeby rysunek dalej był czytelny
plot(X1, ylim = c(-5,5), xlim = c(-2,10), pch = 19, col = "blue", xlab = "X", ylab = "Y", font = 2, asp = 1) abline(v = 0, h = 0, col = "gray") points(X2, pch = 19, col = "orange")
Efekt powinien wyglądać podobnie jak na poniższym rysunku
W podobny sposób można dokonać dyskryminacji w trzech wymiarach. Wykonamy ją dla poniższego zestawu danychX1 <- data.frame(x = c(2, 2, 2, 1, 3, 2, 2), y = c(2, 1, 3, 2, 2, 2, 2), z = c(2, 2, 2, 2, 2, 1, 3)) X2 <- data.frame(x = c(4, 4, 4, 3, 5, 4, 4), y = c(4, 3, 5, 4, 4, 4, 4), z = c(4, 4, 4, 4, 4, 3, 5))
Tym razem, aby otrzymać "trójwymiarowy" rysunek musimy skorzystać z biblioteki scatterplot3d i z dedykowanej funkcji scatterplot3d(). Cała procedura matematyczna jest taka sama jak w poprzednim przypadku, z tą jedynie różnicą, że wektor \(\mathbf{a}=(a_x, a_y, a_z)\) ma trzy składowe, a zamiast prostej dyskryminującej mamy teraz faktycznie płaszczyznę o równaniu
library(scatterplot3d) # Wyznaczenie wartości średnich m1 <- apply(X1, 2, mean) m2 <- apply(X2, 2, mean) # Wyznaczenie macierzy kowariancji S1 <- cov(X1) S2 <- cov(X2) # Liczba elementów klas 1 i 2 oraz ich całkowitej liczba n1 <- nrow(X1) n2 <- nrow(X2) n <- n1 + n2 # Wyznaczenie macierzy zmienności wewnątrzgrupowej W W <- ((n1 - 1) * S1 + (n2 - 1) * S2)/(n - 2) # Wyznaczenie wektora a a <- ginv(W) %*% (m2 - m1) # Wyznaczanie wyrazu wolnego b <- -0.5 * t(a) %*% (m1 + m2)
Inny jest natomiast formalizm rysowania punktów. Najpierw korzystamy z funkcji scatterplot3d(), aby wykreślić punkty pierwszej klasy. Efekt działania funkcji umieszczamy w zmiennej, a następnie wykorzystując wewnętrzne funkcje points3d() oraz plane3d() dodajemy odpowiednio punkty drugiej klasy, a także płaszczyznę. Aby podobnie jak w przypadku 2D umieścić numery klas na punktach, musimy się posłużyć funkcją xyz.convert(), która rzutuje współrzędne 3D na 2D.
# Rysowanie punktów klasy 1 s3d <- scatterplot3d(X1, pch = 21, color = "#AAAAAA", bg = "#EEEEEE", cex.symbols = 3, xlim = c(0, 5), ylim = c(0, 5), zlim = c(0, 5), angle = 123) # Rzutowanie współrzędnych punktów z 3D na 2D X1.coords <- s3d$xyz.convert(X1) X2.coords <- s3d$xyz.convert(X2) # Tekst dla punktów klasy 1 text(X1.coords, "1", col = "blue", font = 2) # Kreslenie hiperplaszczyzny s3d$plane3d(-b / a[3], -a[1] / a[3], -a[2] / a[3], draw_lines = F, draw_polygon = T, polygon_args = list(col = rgb(1, 1, 0, 0.4))) # Rysowanie punktów klasy 2 s3d$points3d(X2, pch = 21, col = "#AAAAAA", bg = "#EEEEEE", cex = 3) # Tekst dla punktów klasy 2 text(X2.coords, "2", col = "orange", font = 2)
FinalnieMetodę Fishera można uogólnić na wiele klas. Posłuży nam ona do analizy poniższego przykładu
Dla wielu klas wektor \(\mathbf{a}\) maksymalizuje wyrażenie
gdzie \(\mathbf{B}\) jest macierzą zmienności międzygrupowej, zdefiniowaną jako
przy czym \(\mathbf{m}\) jest średnią po wszystkich punktach (bez rozróżniania klas), \(g\) jest liczbą klas, natomiast \(\mathbf{W}\) zostaje uogólnione jako
Wektor \(\mathbf{a}\) maksymalizujący \(J\) jest wektorem własnym macierzy \(\mathbf{W}^{-1}\mathbf{B}\) odpowiadającym największej wartości własnej.
Podobnie jak w przypadku dwóch klas, zaczynamy od przypisania danych, naniesienia punktów na wykres oraz wyznaczenia średnich, kowariancji oraz liczności klas.
# Przypisanie wartosci do klas X1 <- data.frame(x = c(1, 2, 2, 2, 3), y = c(2, 3, 2, 1, 2)) X2 <- data.frame(x = c(3, 4, 4, 4, 5), y = c(4, 5, 4, 3, 4)) X3 <- data.frame(x = c(4, 5, 5, 5, 6), y = c(6, 7, 6, 5, 6)) X4 <- data.frame(x = c(8, 9, 9, 9, 10), y = c(8, 9, 8, 7, 8)) X5 <- data.frame(x = c(9, 10, 10, 10, 11), y = c(10, 11, 10, 9, 10)) # Nanoszenie punktow na wykres plot(X1, xlim = c(0,12), ylim = c(0,12), pch = 21, col = "#AAAAAA", bg = "#EEEEEE", cex = 3, xlab = "X", ylab = "Y", font = 2, asp = 1) abline(v = 0, h = 0, col = "gray") points(X2, pch = 21, col = "#AAAAAA", cex = 3, bg = "#EEEEEE") points(X3, pch = 21, col = "#AAAAAA", cex = 3, bg = "#EEEEEE") points(X4, pch = 21, col = "#AAAAAA", cex = 3, bg = "#EEEEEE") points(X5, pch = 21, col = "#AAAAAA", cex = 3, bg = "#EEEEEE") text(X1, "1", col = "blue", font = 2) text(X2, "2", col = "red", font = 2) text(X3, "3", col = "darkgreen", font = 2) text(X4, "4", col = "black", font = 2) text(X5, "5", col = "orange", font = 2) # Wyznaczanie srednich w klasach m1 <- apply(X1, 2, mean) m2 <- apply(X2, 2, mean) m3 <- apply(X3, 2, mean) m4 <- apply(X4, 2, mean) m5 <- apply(X5, 2, mean) # Wyznaczanie macierzy kowariancji S1 <- cov(X1) S2 <- cov(X2) S3 <- cov(X3) S4 <- cov(X4) S5 <- cov(X5) # Liczności klas n1 <- nrow(X1) n2 <- nrow(X2) n3 <- nrow(X3) n4 <- nrow(X4) n5 <- nrow(X5) # Ogólna liczność oraz liczba klas n <- n1 + n2 + n3 + n4 + n5 g <- 5
Następnie należy wyznaczyć ogólną średnią \(\mathbf{m}\) oraz macierze \(\mathbf{B}\) i \(\mathbf{W}\)
# Średnia dla wszystkich punktów m <- apply(rbind(X1, X2, X3, X4, X5), 2, mean) # Macierz zmienności międzygrupowej B <- (n1*(m1 - m) %*% t(m1 - m) + n2*(m2 - m) %*% t(m2 - m) + n3*(m3 - m) %*% t(m3 - m) + n4*(m4 - m) %*% t(m4 - m) + n5*(m5 - m) %*% t(m5 - m))/(g-1) # Macierz zmienności wewnątrzgrupowej W <- 1/(n - g)*((n1 - 1) * S1 + (n2 - 1) * S2 + (n3 - 1) * S3 + (n4 - 1) * S4 + (n5 - 1) * S5)
Wreszcie pozostaje wyznaczyć wartości i wektory własne maceirzy \(\mathbf{U} = \mathbf{W}^{-1}\mathbf{B}\), wybrać wektor własny odpowiadający największej wartości własnej oraz wykreślić kierunek.
# Macierz pomocnicza U <- ginv(W) %*% B # Wyznaczenia wartosci i wektorow własnych lambda <- eigen(U) # Wektor własny odpowiadający maksymalnej wartości własnej a <- lambda$vectors[,which.max(lambda$values)] # Rysowanie kierunku a abline(0, a[2] / a[1], col = "violet", lwd = 2)
Pozostaje wreszcie kwestia rzutowania punktów na wybrany kierunek. Można tego dokonać, korzystając z następującej transformacji
gdzie \(A = a_y / a_x\) to współczynnik kierunkowy powyższej prostej.
# Funkcja do rzutowania obserwacji na kierunek a rzutowanie <- function(X, A) { Xz <- (X$y * A + X$x) / (A**2 + 1) Yz <- A * Xz data.frame(x = Xz, y = Yz) } # Wyznaczenie współczynnika kierunkowego prostej A <- a[2] / a[1] # Wykreślanie zrzutowanych punktów points(rzutowanie(X1, A), col = "blue", pch = 19, cex = 1.5) points(rzutowanie(X2, A), col = "red", pch = 19, cex = 1.5) points(rzutowanie(X3, A), col = "darkgreen", pch = 19, cex = 1.5) points(rzutowanie(X4, A), col = "black", pch = 19, cex = 1.5) points(rzutowanie(X5, A), col = "orange", pch = 19, cex = 1.5)
Powinno to dać poniższy efekt