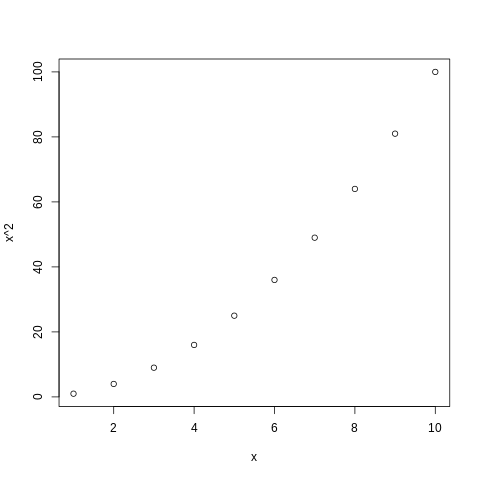
Statystyczna Eksploracja Danych

LABORATORIUM 0



URUCHAMIANIE I KOŃCZENIE SESJI, KOMENDY

INSTRUKCJA PRZYPISANIA

TYPY DANYCH: ATOMOWE

  1. TYP LICZBOWY

    • liczby całkowite i rzeczywiste
    • aby zapisać liczbę calkowitą należy na końcu liczby dodać literę L
    • dozwolona notacja naukowa (np. a <- 2.3e3)
    • separatorem dziesiętnym jest kropka,
    • oprócz tego symbole NaN, Inf, -Inf

    Przykład 0.4
    > a <- 10
> a; typeof(a)
[1] 10
[1] "double"
> b <- 10L
> b; typeof(b)
[1] 10
[1] "integer"
> 1/0
[1] Inf
> exp(-Inf)
[1] 0
> 0 * Inf
[1] NaN

  2. TYP ZNAKOWY

  3. TYP LOGICZNY

    TYPY DANYCH: STRUKTURY DANYCH

  4. WEKTOR

    • uporządkowany zbiór obiektów tego samego typu (wyjątek NA - brak wartości),
    • podstawowy typ w języku R: operacje wykonywane na wektorach są możliwe najbardziej efektywne.

    Metody tworzenia wektorów:

     Możliwe jest indeksowanie wektorów za pomocą nazw elementów:

    Przykład 0.9
    > w <- c(a=1, b=2, c=3)
> w[1]
a 
1 
> w['a']
a 
1 
> w["a"]
a 
1

  5. TYP CZYNNIKOWY (WYLICZENIOWY, KATEGORYCZNY)

  6. LISTA

  7. MACIERZ

  8. RAMKA DANYCH (DATA FRAME)

INDEKSY

Korzystając z operatorów c() (względnie c(-)) oraz : możliwe jest wypisywanie zadanych części

OPERACJE NA WEKTORACH I MACIERZACH

Zdefiniujmy następujące wektory w, u i macierze A, B

Przykład 0.17
> w <- c(1,2); w
[1] 1 2
> v <- c(3,4); v
[1] 3 4
> A <- matrix(1:4, 2, 2); A
     [,1] [,2]
[1,]    1    3
[2,]    2    4
> B <- matrix(4:1, 2, 2); B
     [,1] [,2]
[1,]    4    2
[2,]    3    1

Możemy wykorzystać następujące operacje na wektorach oraz na macierzach

INSTRUKCJE STERUJĄCE

  1. PĘTLA FOR

    Przykład 0.18
    > x <- 1:10
> for(y in x) print(y)
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10

  2. PĘTLA WHILE

    Przykład 0.19
    > x <- 1
> while(x < 5) {
+ print(x)
+ x <- x + 1
+ }
[1] 1
[1] 2
[1] 3
[1] 4

  3. INSTRUKCJA WARUNKOWA IF...ELSE...

    Przykład 0.20
    > x <- 5
> if(x < 5) print(x) else print(x^2)
[1] 25

    Warunek musi mieć długość równą 1, inaczej instrukcja warunkowa zostanie wykonana tylko dla pierwszego elementu

    Przykład 0.21
    > x <- 1:10
> if(x %% 3) print("Nie dzieli sie przez 3") else print("Dzieli sie przez 3")
[1] "Nie dzieli sie przez 3"
Warning message:
In if (x%%3) print("Nie dzieli sie przez 3") else print("Dzieli sie przez 3") :
  the condition has length > 1 and only the first element will be used

  4. INSTRUKCJA WARUNKOWA IFELSE(WARUNEK, INSTRUKCJA1, INSTRUKCJA2)

    Przykład 0.22
    > x <- 1:10
> ifelse(x %% 3, "Nie dzieli sie przez 3", "Dzieli sie przez 3")
 [1] "Nie dzieli sie przez 3" "Nie dzieli sie przez 3" "Dzieli sie przez 3"    
 [4] "Nie dzieli sie przez 3" "Nie dzieli sie przez 3" "Dzieli sie przez 3"    
 [7] "Nie dzieli sie przez 3" "Nie dzieli sie przez 3" "Dzieli sie przez 3"    
[10] "Nie dzieli sie przez 3"

FUNKCJE

 Schemat tworzenia funkcji jest następujący 

nazwa_funkcji <- function(x, y, ...) {
...
...
return(wartosc)
}

Przykładem może być funkcja realizująca "tabliczkę mnożenia" dla dowolnych dwóch wektorów

Przykład 0.23
> tabliczka_mnozenia <- function(zakres1, zakres2) {
+ return(zakres1 %o% zakres2)
+ }
> tabliczka_mnozenia(1:10,1:10)
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    1    2    3    4    5    6    7    8    9    10
 [2,]    2    4    6    8   10   12   14   16   18    20
 [3,]    3    6    9   12   15   18   21   24   27    30
 [4,]    4    8   12   16   20   24   28   32   36    40
 [5,]    5   10   15   20   25   30   35   40   45    50
 [6,]    6   12   18   24   30   36   42   48   54    60
 [7,]    7   14   21   28   35   42   49   56   63    70
 [8,]    8   16   24   32   40   48   56   64   72    80
 [9,]    9   18   27   36   45   54   63   72   81    90
[10,]   10   20   30   40   50   60   70   80   90   100

Instrukcja return() nie jest obligatoryjna - za wartość funkcji przyjmowana jest wartość wyznaczona w ostatniej jej linii

Przykład 0.24
> dodaj <- function(x, y) {
+ x*y
+ cos(x)
+ x+y
+ }
> dodaj(2,5)
[1] 7

Wszystkie wartości przekazane do funkcji są widoczne i zmieniane lokalnie. W przypadku potrzeby zmiany wartości zmiennej tak, aby była widoczna globalnie należy użyć operatora przypisania <<-

Przykład 0.25
> f <- function(x, y) {
+ x <- x * 2
+ y <<- y * 2
+ }
> x <- 2
> y <- 2
> f(2,2)
> x
[1] 2
> y
[1] 4

SKRYPTY

 Skrypty w języku R uruchamiane są komendą source("nazwa_pilku"). Oczywiście, w przypadku używania własnych funkcji, należy je zdefiniować przed główną częścią skryptu, czyli po prostu na górze. W odróżnieniu od linii komend, wypisanie na ekran trzeba ubrać w odpowiednią funkcję print() lub cat().

Plik test.R
# Funkcja 
f <- function(x, y) {
  x <- 2*x
  y <<- 2*y
}

# Główna część skryptu

x <- 2
y <- 2

print(x)
print(y)
x

f(2,2)

cat("x =",x,"\n")
cat("y =",y,"\n")

Przykład 0.26
> source("test.R")
[1] 2
[1] 2
x = 2 
y = 4

FUNKCJE OBSŁUGI WEKTORÓW

 Następujące funckcje są bardzo przydatne podczas obsługi danych w formacie wektorowym: Również często wykorzystywanymi funkcjami są

FUNKCJE OBSŁUGI MACIERZY

 Część powyższych funkcji można zastosować także do macierzy, przy czym w przypadku which.min() oraz which.max() konieczne jest użycie dodatkowo funkcji arrayInd() do określenia indeksów macierzy - w przeciwnym wypadku otrzymamy tylko indeks "wektorowy".

Przykład 0.34
> A <- matrix(1:16, 4, 4)
> A
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16
> sum(A)
[1] 136
> mean(A)
[1] 8.5
> sd(A)
[1] 4.760952
> min(A)
[1] 1
> max(A)
[1] 16
> which.min(A)
[1] 1
> which.max(A)
[1] 16
> arrayInd(which.min(A), dim(A))
     [,1] [,2]
[1,]    1    1
> arrayInd(which.max(A), dim(A))
     [,1] [,2]
[1,]    4    4

Aby wyznaczyć brzegowe wartości dla macierzy (np. sumę, średnią etc) wykorzystuje się funkcję apply(macierz,liczba,funkcja), przy liczba określa, czy odnosimy się do wiersza (1), kolumny (2) itd.

Przykład 0.35
> A
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16
> apply(A, 1, sum)
[1] 28 32 36 40
> apply(A, 2, sum)
[1] 10 26 42 58
> apply(A, 1, mean)
[1]  7  8  9 10
> apply(A, 2, sd)
[1] 1.290994 1.290994 1.290994 1.290994

Zamiast wbudowanych funkcji można także wykorzystać funkcje zbudowane przez siebie

Przykład 0.36
> sum.x2 <- function(x) {
+ sum(x^2)
+ }
> apply(A, 1, sum.x2)
[1] 276 336 404 480
> apply(A, 2, sum.x2)
[1]  30 174 446 846

Natomiast w celu zastosowania dowolnej funkcji do każdego elementu macierzy, należy użyć komendy sapply()

Przykład 0.37
> sapply(A, sum.x2)
 [1]   1   4   9  16  25  36  49  64  81 100 121 144 169 196 225 256

Istnieje również możliwość stworzenia tzw. funkcji anonimowej, którą definiujemy w locie.

Przykład 0.38
> a <- 1:10
> sapply(a, function(x) {x^2 - 2})
 [1] -1  2  7 14 23 34 47 62 79 98

Funkcje sapply() można zagnieżdżać, tworząc alternatywę dla wielokrotnych pętli

Przykład 0.39
> a <- 1:10
> sapply(a, function(x) { sapply(rev(a), function(y) { x * y }) } )
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]   10   20   30   40   50   60   70   80   90   100
 [2,]    9   18   27   36   45   54   63   72   81    90
 [3,]    8   16   24   32   40   48   56   64   72    80
 [4,]    7   14   21   28   35   42   49   56   63    70
 [5,]    6   12   18   24   30   36   42   48   54    60
 [6,]    5   10   15   20   25   30   35   40   45    50
 [7,]    4    8   12   16   20   24   28   32   36    40
 [8,]    3    6    9   12   15   18   21   24   27    30
 [9,]    2    4    6    8   10   12   14   16   18    20
[10,]    1    2    3    4    5    6    7    8    9    10

TWORZENIE WYKRESÓW

 Standardową funkcją wykorzystywaną do tworzenia wykresów jest plot(x,y), gdzie x i y są odpowiednio wektorami liczb.

Przykład 0.40
> x <- 1:10
> plot(x, x^2)

Funkcja plot() ma pokaźny zestaw różnych opcji, przy czym najczęściej wykorzystywane to xlab="..." (tytuł osi X), ylab="..." (tytuł osi Y), main="..." (tytuł wykresu), col="..." (kolor punktów), pch=... (kształt punktów), cex="..." (rozmiar punktów), font=... (typ czcionki osi: 1 - normalna, 2 - pogrubiona, 3 - kursywa, 4 - pogrubiona kursywa). W przypadku nazw osi można wykorzystywać funkcję expression(), która koduje wyrażenia matematyczne i litery greckie (np. ^ to indeks górny, [..] - indeks dolny, itd.).

Przykład 0.41
> x <- 1:10
> plot(x, x^2, xlab="x", ylab=expression(f(xi)==x^2), col="red", 
pch=19, font=2, font.lab=4, main="Wykres funkcji f(x)", font.main=3, cex=2)

W przypadku potrzeby zapisania wykresu do pliku należy skorzystać z jednej z komend png(), jpeg() czy tiff(), a następnie zamknąc strumień komendą dev.off().

Przykład 0.42
> png("fig2.png")
> plot(x, x^2, xlab="x", ylab=expression(f(xi)==x^2), col="red", 
pch=19, font=2, font.lab=4, main="Wykres funkcji f(x)", font.main=3, cex=2)
> dev.off()

Aby do istniejącego wykresu dodać kolejne serie danych należy użyć funkcji points() (dodawanie punktów), lines() (dodawanie linii) lub abline() (tworzenie prostych o zadanych współczynnikach kierunkowych np. y = x + 2 abline(a = 2, b = 1) czy też prostych poziomych np. y=10 abline(h=10) lub pionowych np x=5 abline(v=5).

Przykład 0.43
> plot(x, x^2, xlab="x", ylab=expression(f(xi)==x^2), col="red", pch=19, font=2, font.lab=4, main="Wykres funkcji f(x)", font.main=3, cex=2)
> points(x, 100-x^2, col="blue", pch=3, cex=1.5)
> lines(y <- seq(1,10,0.01), 500*sin(5*y)*exp(-y), col="green", lwd=2)
> abline(h=60, v=6, lwd=2, col="gray", lty=2)
> abline(a=100, b=-10, lwd=3, lty=3, col="orange")

TWORZENIE HISTOGRAMÓW

 Najprostszą metodą tworzenia histogramu jest wykorzystanie funkcji tabulate(), przy efektem jej działania jest zliczenie wartości całkowitych zawartych w wektorze. W przypadku liczb rzeczywistych doknywane jest zaokrąglenie w dół.

Przykład 0.44
> y <- c(0,0,1,2,3,1,2,3,4)
> tabulate(y)
[1] 2 2 2 1
> y <- c(0,0,1.1,1.9,2.1,2,3)
> tabulate(y)
[1] 2 2 1

W przypadku histogramu 2D można posłużyć się funkcją table(), która stworzy dwuwymiarową tablicę współwystępowania wartości.

Przykład 0.45
> df <- data.frame(x=c(1,1,2,2,3,4,5), y=c(2,2,3,1,5,5,5))
> df
  x y
1 1 2
2 1 2
3 2 3
4 2 1
5 3 5
6 4 5
7 5 5
> table(df)
   y
x   1 2 3 5
  1 0 2 0 0
  2 1 0 1 0
  3 0 0 0 1
  4 0 0 0 1
  5 0 0 0 1

Jednak klasyczną funkcją odpwiedzialną za tworzenie histogramów jest hist(). Samo jej wywołanie daje efekt wyrysowania histogramu o zadanej liczbie przedziałów (binów).

Przykład 0.46
> x <- c(1,1,1,2,2,4,10)
> hist(x)

W pewnym sensie nawet ważniejszą rzeczą od samego wykresu jest zawartość zmiennej, do której zostanie zapisany jego wynik. Otrzymamy z niej informacje nie tylko o liczbie zliczeń ($counts), ale także o granicach binów ($breaks), ich środkach ($mids) jak również funkcji gęstości ($density).

Przykład 0.47
> x <- c(1,1,1,2,2,4,10)
h <- hist(x)
> h
$breaks
[1]  0  2  4  6  8 10

$counts
[1] 5 1 0 0 1

$density
[1] 0.35714286 0.07142857 0.00000000 0.00000000 0.07142857

$mids
[1] 1 3 5 7 9

$xname
[1] "x"

$equidist
[1] TRUE

attr(,"class")
[1] "histogram"

LOSOWANIE WARTOŚCI

WCZYTYWANIE DANYCH Z PLIKU

 Jedną z najczęściej wykorzystywanych funkcji do wczytywania danych z pliku jest read.table(), tworząca z wczytanego zbioru ramkę danych. Oznacza to, że w pliku każda linia powinna zawierać tyle samo pól, a poza tym każda kolumna musi zawierać ten sam typ danych.

Plik test1.dat
1 "Patient 1" 2 0.5
20 "Patient 10" 10 0.11111
30 "No name" 1 0.99

Przykład 0.51
> df <- read.table("test1.dat")
> df
  V1         V2 V3      V4
1  1  Patient 1  2 0.50000
2 20 Patient 10 10 0.11111
3 30    No name  1 0.99000

W przypadku, gdy chcemy nadać nazwy poszczególnym kolumnom ramki, podajemy opcję read.table(col.names="..."). Spacje w nazwach zostaną zastąpione kropkami.

Przykład 0.52
> df <- read.table("test1.dat", col.names=c("id", "name", "degree", "clust coeff"))
> df
  id       name degree clust.coeff
1  1  Patient 1      2     0.50000
2 20 Patient 10     10     0.11111
3 30    No name      1     0.99000
> df$degree
[1]  2 10  1

Inną opcją jest podanie nazw kolumn w samym pliku - jeśli w pierwszym wierszu jest o jedno pole mniej niż w kolejnym, funkcja automatycznie potraktuje pierwszą linię jako nazwy kolumn, natomiast pierwszą kolumnę jako nazwy wierszy.

Plik test2.dat
name degree cluster
1 "Patient 1" 2 0.5
20 "Patient 10" 10 0.11111
30 "No name" 1 0.99

Przykład 0.53
> df <- read.table("test2.dat")
> df
         name degree cluster
1   Patient 1      2 0.50000
20 Patient 10     10 0.11111
30    No name      1 0.99000
> colnames(df)
[1] "name"    "degree"  "cluster"
> rownames(df)
[1] "1"  "20" "30"

ZAPISYWANIE DANYCH DO PLIKU

 W przypadku macierzy oraz ramek danych odpowiednim sposobem zapisu danych jest użycie funkcji write.table(). W przypadku, gdy dane mają być "czyste" (bez nazw kolumn i wierszy), używamy opcji write.table(col.names=F, row.names=F)

Przykład 0.54
> df <- data.frame(x=1:3, names=c("Aaaa", "Bbbb", "Ccc"))
> df
  x names
1 1  Aaaa
2 2  Bbbb
3 3   Ccc
> write.table(df, "test4.dat")
> A <- matrix(1:10, 2, 5)
> write.table(A, "test5.dat")
> write.table(A, "test5.dat", row.names=F, col.names=F)

Istnieje bezpośrednia metoda, polegająca na zapisaniu zmiennej do pliku poprzez instrukcję save(). W ten sposób nie trzeba się zastanawiać nad formatem zapisu.

Przykład 0.55
> a
[[1]]
[1] "1" "2" "3" "4" "5" "6" "7" "8"

[[2]]
[1] "a"     "cos"   "jakis"

> save(a, file="a")
> ls()
[1] "a"    "A"    "aa"   "dane" "df"   "L"    "x"   
> rm(a)
> ls()
[1] "A"    "aa"   "dane" "df"   "L"    "x"   
> a
Error: object 'a' not found
> load("a")
> a
[[1]]
[1] "1" "2" "3" "4" "5" "6" "7" "8"

[[2]]
[1] "a"     "cos"   "jakis"

REGRESJA LINIOWA

 W wielu przypadkach interesuje nas wykonanie analizy regresji opracowywanych danych. W pakiecie R służy do tego funkcja lm(), przy czym specyficzny jest sposób wprowadzania formuły - w R wykorzystuje się symbol tyldy ~ do pokazania zależności pomiędzy zmiennymi (np. y ~ x oznacza zależność pomiędzy x i y. Poniżej generujemy zaburzoną losowo zależność liniową

Przykład 0.56
> x <- 1:20
> y <- 2*x-2 + runif(length(x), -3, 3)
> x
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
> y
 [1] -2.9533514  0.2321698  5.2192884  7.5458593  8.7547771 11.3795559
 [7] 13.2345637 15.6031631 18.3817310 16.7632322 18.9254405 22.3293603
[13] 23.7654302 26.9699065 25.2812426 30.8505703 29.7152427 33.7703004
[19] 34.7156642 36.8997098
> plot(x, y)

Wykonujemy regresję liniową i wynik procedury zapisujemy do zmiennej xy.lm. Po wywołaniu funkcji summary() otrzymamy wszystkie interesujące nas wartości dotyczące regresji. Bezpośrednie odwołanie do współczynników otrzymujemy poprzez pole coefficients, przy czym coefficients[1] to punkt przecięcia, a coefficients[2], to współczynnik kierunkowy. Możemy następnie zapisać współcznniki i wyreślić prostą dopasowania.

Przykład 0.57
> xy.lm <- lm(y ~ x)
> summary(xy.lm)

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.4009 -0.9691  0.4542  1.2475  2.4212 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.49155    0.73606  -2.026   0.0578 .  
x            1.93912    0.06145  31.558   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.585 on 18 degrees of freedom
Multiple R-squared:  0.9822,    Adjusted R-squared:  0.9813 
F-statistic: 995.9 on 1 and 18 DF,  p-value: < 2.2e-16
> xy.lm$coefficients
(Intercept)           x 
  -1.491550    1.939118
> b <- xy.lm$coefficients[1]
> a <- xy.lm$coefficients[2]
> plot(x, y, pch=19)
> lines(x, a*x+b, col="red", lwd=3)

Podobną procedurę można przeprowadzić dla przetransformowanych zmiennych. Tutaj jest to "zrandomiznowana zależność" y ~ x-2.

Przykład 0.58
> x <- c(1,2,5,10,20,50,100,200,500,1000)
> y <- (x*(1+runif(length(x),-0.9,0.9)))^(-2)
> plot(x, y, log="xy")
> xy.lm <- lm(log(y) ~ log(x))
> summary(xy.lm)

Call:
lm(formula = log(y) ~ log(x))

Residuals:
    Min      1Q  Median      3Q     Max 
-1.1943 -0.9342 -0.2273  0.9106  1.5951 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.02597    0.63814   0.041    0.969    
log(x)      -2.02940    0.15557 -13.045 1.13e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.089 on 8 degrees of freedom
Multiple R-squared:  0.9551,    Adjusted R-squared:  0.9495 
F-statistic: 170.2 on 1 and 8 DF,  p-value: 1.132e-06

> b <- exp(xy.lm$coefficients[1])
> a <- xy.lm$coefficients[2]
> plot(x, y, pch=19, log="xy")
> lines(x, b*x^a, col="red", lwd=3)