| Lecture presented at the workshop "Complex Systems in Natural and Social Sciences" (CSNSS’99), 14-17 September 1999, Kazimierz Dolny, Poland |
Minimum of Entropy Generation as a General Evolution Criterion
for Nonlinear Structured Systems with Fixed Boundaries
Stanislaw Sieniutycz
Faculty of Chemical and Process Engineering, Warsaw University of Technology,
00-645 Warsaw, 1 Warynskiego Street, Polan
d (sieniutycz@ichip.pw.edu.pl)
The purpose of our presentation is a general thermodynamic framework for balance and kinetic equations of structured heterogeneous systems and chemical networks which is consistent with the second law of thermodynamics. Methods effective in classical irreversible thermodynamics of single-phase systems are here extended to include boundary discontinuities, surface reactions and interface transports in multiphase systems. Complex multiphase and multireaction systems are analyzed by methods of the network (system) theory in which topological and graphical methods of electrical networks are extended to quite general energo-chemical systems. Chemical Ohms law links chemical force (affinity) and chemical flux (reaction rate), and chemical conversions follow simple rules of the algebra for chemical resistances. There are two main methods coming from thermodynamics of single-phase systems, which can effectively be applied to complex structured systems. The first method starts with the derivation of balance equations for mass, energy and momentum and terminates at the entropy balance; from the knowledge of the entropy source
ss kinetic laws are postulated. Yet, our main objective is the second (newer) method which is based on the variational formulation of second law and concept of nonlinear chemical resistance. It is an optimization method in which an entropy functional is minimized to predict kinetic laws and secure appropriate balance equations. The method does not postulate linearity; rather it rests on state-dependent dissipation functions. It follows that the variational method assures classical nonlinear kinetics of mass action and nonlinear set of diffusion-reaction equations under the condition of local thermal equilibrium. Still local disequibria can be predicted which are shown to be responsible for onset of interfacial and bulk instabilities. Hamiltonian form of transport equations and laws of chemical kinetics is valid, which is efficient to accommodate nonlinear effects.This communication sets a general thermodynamic framework for balance and kinetic equations of multiphase reacting systems in the way consistent with the second law of thermodynamics. Approaches effective in the contemporary theory of nonequilibrium thermodynamics of single-phase systems are here extended to include interfacial discontinuities, surface reactions and interface transports which are phenomena characteristic of multiphase systems. We arrive at Hamiltonian structures of exchange and transport equations and laws of chemical kinetics, which consitute efficient forms serving to generalize linear models to nonlinear regimes. Local disequibria are predicted which are shown to be resposible for onset of interfacial and bulk instabilities.
There are two main approaches coming from thermodynamics of single-phase systems. The first (older) approach starts with the derivation of balance equations and terminates at the formulation of a related expression for the entropy production. In this approach balance equations are first derived for mass, energy and momentum, and the combination of the energy and momentum equations leads to a balance equation for the internal energy. This internal energy balance is next combined with the Gibbs equation which describes the entropy as the state function. The result is an equation for entropy balance. From its source term kinetic laws can be postulated. Approach of this sort was extended to multiphase systems by several researchers: G. Standard (Chisa Prooceedings pp. 37-48, 1962; Chem. Eng. Sci. 19, 227-236, 1964) who applied to heterogeneous systems integral transformation theorems in the manner similar to that developed by R. B. Bird (Chem. Eng. Sci. 6, 123-128, 1957) for the homogeneous case.

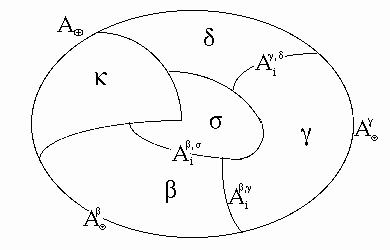
Fig. 1
: Scheme of a general multiphase system and principle of designations.
Further contributions of this sort are by Slattery group (Deemer, A. R. and Slattery J., Int. J. Multiphase Flow 4, 171-192, 1978 and Chem. Eng. Commun. 4, 149-166, 1980; Slattery, J., Interfacial Transport Phenomena, Springer, Berlin 1992. A statistical mechanics approach was recently applied to derive multiphase flow equations from a modified Boltzmann equation by the Chapman-Enskog technique (Zou, Q., and He, X., Phys Rev. E 59, 1253-1255, 1999.
The main objective of our presentation is the second (newer) approach which is based on the variational formulation of second law and the concept of nonliear chemical resistance. It is, in fact, quite recent, and it is unknown to date in the context of multiphase systems. For single-phase systems it was developed in works of Sieniutycz and Berry (Phys Rev. A, 46, 6359, 1992) who extended to physical four-dimensional space-time the original Onsager-Gyarmati approach applicable in an exact way only to three-dimensional spaces and steady processes. We pursue an optimization approach in which an entropy functional is minimized to get kinetic laws along with recovered balance equations. The approach does not postulate linearity; rather it rests on the state-dependent dissipation functions from the beginning. In view of these positive features, in spite of some mathematical difficulty, we apply this approach to multiphase systems. We outline related derivations below. They are restricted to systems in mechanical equilibrium which may move with a constant barycentric velocity v.
Each phase is an open, multicomponent system, of n components and N chemical reactions
The system contains species i with chemical potential
mi; T is the local temperature, and R the gas constant. The nand nare the forward and backward stoichiometric coefficients, respectively, for species i in reaction j. The advancement of the jth reaction is denoted by xj, and its rate rj. Each phase can be thermally inhomogeneous. The notation for the vector set in each phase (phase superscript a omitted) is as follows![]()
![]()
![]()
with ![]() and the
entropic capacitance matrix
and the
entropic capacitance matrix ![]()
Complex multiphase and multireaction systems can effectively by analyzed by methods developed in the network (system) theory. These methods extend topological and graphical methods of electrical networks to quite general energy and chemical systems. In such approaches chemical conversion follows rules of the algebra for chemical resistances, R. Chemical Ohms law links the chemical force (affinity) and chemical flux (reaction rate). Using chemical resistances is simple. An example is given below.
Consider a system of enzyme reactions (3 reactions between 4 components)
![]()
![]()
![]()
aiming to evaluate the total conversion of s into p,
xT. There are two consecutive channels (1 and 2) and one parallel channel (3). For the total conversion xT Shiner (Adv. in Thermodyn. 6, 248, 1992) finds![]()
where the superscript e refers to chemical potentials, fixed
in an external world. (In the stationary state ![]() .).
It is essential that all R
.).
It is essential that all R
The variational form of the second law in the multiphase system has the general structure
![]()
where ![]() is the
total entropy production which comprizes the effect of bulks and interfaces.
Each of quantities,
is the
total entropy production which comprizes the effect of bulks and interfaces.
Each of quantities, ![]() or
or ![]() is positive. Otherwise
is positive. Otherwise ![]() is the
entropy exchanged by the system with its external word and its sign is
undetermined. Equation (7) provides the physical interpretation for the
variational formulation of the second law (8) which proves that the entropy
plays a role in thermodynamics similar to that of action in mechanics. The
governing variational principle is set in the physical space-time rather than in
the three-dimensional space and, as such, it substantiates the role of the
entropy rather than the entropy production. For the prescribed states and/or
fluxes at the system boundary (constant
is the
entropy exchanged by the system with its external word and its sign is
undetermined. Equation (7) provides the physical interpretation for the
variational formulation of the second law (8) which proves that the entropy
plays a role in thermodynamics similar to that of action in mechanics. The
governing variational principle is set in the physical space-time rather than in
the three-dimensional space and, as such, it substantiates the role of the
entropy rather than the entropy production. For the prescribed states and/or
fluxes at the system boundary (constant ![]() )
the principle implies a least possible production of entropy under constraints
imposed by conservation laws. We shall show that equations of transport,
chemical kinetics and conservation laws follow from this entropy principle
subject the conservation law constraints.
)
the principle implies a least possible production of entropy under constraints
imposed by conservation laws. We shall show that equations of transport,
chemical kinetics and conservation laws follow from this entropy principle
subject the conservation law constraints.
As first recognized by Onsager, for the purpose of variational formulation the entropy production has to be expressed as the sum of two dissipation functions, the first depending on fluxes and the second on forces. When viscous phenomena are ignored and the problem is restricted to known constant velocities in each phase, the second law functional can be stated as
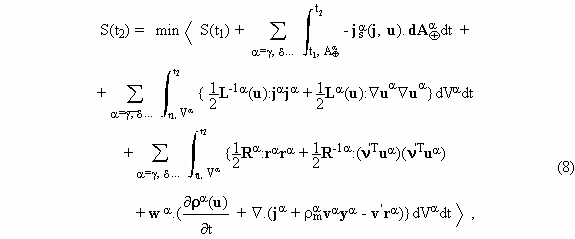
where the Lagrange multipliers w adjoint constraints
required by balance equations. In this formula, the first line contains the sum
of the surface integrals over closed areas, ![]() ,
which surround separate phases existing in the system. The subscript
,
which surround separate phases existing in the system. The subscript ![]() stresses their closed and oriented nature. In our notation, the entropy flux j
stresses their closed and oriented nature. In our notation, the entropy flux j
In accordance with Fig. 1, the sum of all closed surface
integrals can be split into components. The first surface component is the
(single) closed integral over the system external area, ![]() ,
,

It represents the exchange of entropy with an external word in the time t
2-t1. The second surface component is the sum of non-closed surface integrals over the internal areas or interfaces,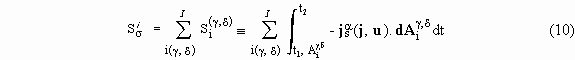
For steady interfaces, this integral sum is equal to the entropy produced due to interfaces. The entropy is also produced in bulks of each phase; this phenomenon is represented by the integral
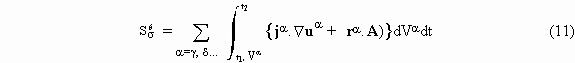
The expressions in the first term refer to transport processes and those in the second to chemical reactions.
For systems in which interface reactions are absent the dissipation function representation of the entropy production for interfaces is
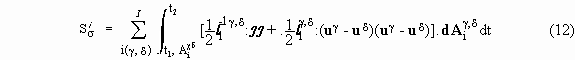
whereas for the bulk
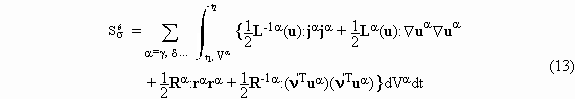
The expressions in the first line refer to transport processes and those in the second line to chemical reactions. These two integrals enable one to apply the variational principle in question; their sum is, in fact, contained in the functional (8).
Let us compare results of the macroscopic balance approach and of the variational approach in the bulk of each phase for the case of the resting system in mechanical equailibrium (ignored effects of hydrodynamic motion). In the matrix notation, the macroscopic balance approach yields the set of Eqs. (14)-(16). It respectively contains the conservation laws, and (postulated by the entropy source analysis) standard linear laws of coupled Onsager transport with first laws of Fourier and Fick incorporated, and linear chemical kinetics. An extra (dependent) equation of the set is a matrix equation of change obtained as the combination of conservation and kinetic equations. With the neglected phase superscript,
a, the complete set is![]()
![]()
![]()
where c(u)= - ∂
r(u)/∂u is the capacity matrix and As = n'Tu is the vector of affinities. Both these quantities are in the entropy representation. The conservation laws (14) contain production terms which are nonvanishing for i=1,...n. The formal macroscopic balance approach and the related linear kinetics predicted from the entropy source are not capable of assuring any nontrivial information about true, nonlinear chemical kinetics. On the other hand, the result of vanishing of the first variation of the entropy source Ss or the Euler-Lagrange equations of the functionals (28) or (37) with respect to the variables w, j, r and u are respectively the nonlinear equations![]()
![]()
![]()
To prove that the true chemical kinetics is now assured, we first use the fact that the equilibrium constant for the jth reaction Kj is given by the ratio of the forward and backward reaction rate constants, k
jf/kjb; then the entropic chemical affinity of the jth reaction can be expressed in the formNext we use the definition of the chemical resistances, that obey the formula
(Grabert et al.:Physica 117A, 300, 1983; Shiner J. Chem. Phys. 87, 1089, 1987; Sieniutycz, Chem. Engng Sci. 42, 2697, 1987) with the activities ai = ai(
r) expressed as functions of the actual state. With these relations, it follows from Eqs. (18) and (19) that the variational method assures classical nonlinear kinetics and nonlinear set of diffusion-reaction equation under the subsidiary condition of local thermal equailibrium, i.e. when u=w. This proves that the variational approach is reacher than that based on balance equations; once the variational principle is stated it lives its own life and, whenever suitable nonlinear resistances are applied, true nonlinear chemical kinetics (described by Guldberg and Waage kinetics, Langmuir kinetics, or other formulae) can be secured along with nonlinear diffusion-reaction sets. The distinction between the Gibbsian intensities u and Lagrange multipliers of conservation laws w plays, in particular, a role in explaining the origin and development of thermo-hydrodynamic instabilities by tracing the growing differences between the Gibbsian intensities u and w on unstable trajectories.
Podziękowanie
Prace wykonano w ramach grantu dziekańskiego Nr 503/0007/009, rok 1999.