Formation of opinions under the influence of competing agents - a mean field approach

Krzysztof Kacperski¹, Janusz A. Holyst²

Abstract

1  Introduction

Interdisciplinary research has been drawing much attention in the last decades. Models and methods developed in theoretical physics proved to be fruitful in studying complex systems [,], composed of relatively simple mutually interacting elements, coming from domains as diverge as neural networks [], disease spreading [], population dynamics [], etc. But the range of the investigations goes also beyond the natural sciences and includes problems from sociology or economy, like e.g. pedestrian motion and traffic [], migrations [,], financial crashes [].

Another important subject of this kind is the process of opinion formation in social groups or decision making, also at the level of whole countries. One way of its quantitative description consists in a macroscopic approach based on the master equation or the Boltzmann-like equations for global variables [,,]. Alternatively, by making some sociologically motivated assumptions on the mechanisms of interactions between individuals ``microscopic'' models are constructed and investigated numerically and analytically by means of the methods known from statistical physics [,]. One concludes that the variety of the emerging collective phenomena has much in common with the complex social processes.

One of the examples is the class of models based on the concept of cellular automata [] and the theory of social impact formulated by Latané [], and conformed in a number of sociological studies [,]. Different variants of the model were explored numerically [,], and many of the observations were than explained in the framework of a mean field approach [] and recently the Landau theory []. An extention of the model introducing the time variance of the social strengths of individuals according to some learning rule has also been studied []. The essential outcome of both the theory and simulations is the onset of clusters of minority that can survive within the majority holding the opposite opinion and be persistent throughout long periods of dynamics. It has been indicated that strong individuals play an important role in the formation and stability of the clusters. Motivated by this, in [,,] we considered a particular case of the model, namely when a strong individual (a leader) is present in the social group. Multistability and hysteresis phenomena, as well as different kinds of rapid changes (phase transitions) in the distribution of opinions were encountered.

Here the effects of competition between the strong leader and an external influence or preference acting homogeneously within the group are studied in terms of a mean field approach. We show that such antagonism can lead not only to sudden changes of opinion, but also to the critical behaviour. The high ``social temperature'' reveals the dominance of the stronger agent. After introducing the model (section ) and recalling some results for the deterministic case (section ) we investigate in detail the noise induced transitions giving rise to the critical behaviour (section ).

2   Model of a social group

Our system consists of N individuals (members of a social group); we assume that each of them can share one of two opposite opinions on a certain subject, denoted as s_i = ±1,  i = 1,2,...N. Individuals can influence each other, and each of them is characterised by the parameter s_i > 0 which describes the strength of his/her influence. Every pair of individuals (i,j) is ascribed a distance d_ij in a social space. The changes of opinion are determined by the social impact exerted on every individual:

Opinions of individuals change simultaneously (synchronous dynamics) in discrete time steps according to the rule

Our model social space is a 2D disc of radius R with the individuals located in the nodes of quadratic grid; the distance between nearest neighbours equals 1, and each node is occupied with probability r which may be also regarded as a constant surface density of individuals. The geometric distance models the social immediacy. Strength parameters s_i of the individuals are positive random numbers with probability distribution q(s) and the mean value [`(s)]. In the centre of the disc there is a strong individual (whom we will call the ``leader''); his/her strength s_L is much greater than that of all the others (s_L >> s_i).

3  Deterministic limit

Let us first recall the properties of the system without noise, i.e. at T = 0 (see [,] for details). The dynamical rule (2) becomes then strictly deterministic: s_i(t+1) = -sign(I_i s_i), so the condition for the stability of a state is I_i < 0 for every i. To proceed with the calculations we used the approximation of continuous distribution of individuals replacing the sum in (1) by an integral. In the stationary state the impact is maximal, almost equal zero, at places where individuals of opposite opinion abut, so the condition

Considering the possible stationary states in our model we find the trivial unification (with equal opinion for each individual) or, due to the symmetry, a circular cluster of individuals sharing the opinion of the leader surrounded by a ring of their opponents (the majority). These states remain stationary also for small self-support parameter b; for sufficiently large b any configuration may remain ``frozen''.

As far as the shape of the cluster is known, the impact I(x,y) at its border can be calculated and then (3) is the equation for the radius of stationary clusters. Typically it has two real solutions: the smaller corresponding to the stable cluster and the larger one - to the unstable cluster, which is actually the separatrix between basins of attraction of the stable cluster and the state of unification. Owing to the nonzero self-support parameter b in (1) reflecting the inertia of individuals in changing their minds (it may be regarded as an analogy of the dry friction in mechanical systems), both solutions form in fact a kind of bands; the states within the bands are ``frozen''. In this way also the unstable clusters can be observed at b > 0 and appropriately chosen initial conditions.

When the strength of the leader s_L or the external impact h supporting the opinion of the leader is increased the size of the stable cluster grows, and at some critical point both real solutions of (3) collide. Then the equation has no longer real solutions and the unification is the only stable state. At the critical point one observes a discontinuous phase transition: cluster ® unification. If a strong persuasive external impact acts on a unified group, in inverse transition unification ® cluster is possible.

4  Noisy dynamics

In the presence of noise the borders of the stable clusters become diluted, i.e. individuals of both opinions appear all over the group. Considering the dynamics (2) we can conclude that the influence of noise on a single individual depends on the ratio I_i/T. Because of the strong influence of the leader, the supportive (negative) impact is stronger inside the cluster than outside it. Thus, due to noise induced flips of opinions the adherents of the leader appear more often outside the cluster (among the majority of opponents) than the opponents inside it. Moreover the area outside is much greater than that of the cluster itself, so we observe the effective growth of the minority group. This causes that the supportive impact outside the cluster becomes still weaker and the majority becomes more sensitive to random changes; it is a kind of positive feedback. At a certain value of temperature the process becomes avalanche-like and the former majority disappears. Thus noise induces a jump from one attractor (cluster) to another (unification). Such a transition is possible at every non-zero temperature but its probability remains very small until the noise level exceeds a certain critical value. Our simulations prove that it is indeed a well defined temperature that separates two phases (i.e. two attractors). Similarly the transition unification ® cluster in the presence of external impact can be induced by noise.

4.1  Mean field approximation. Phase transitions, critical dynamics

We can derive analytically the stationary states of the system an nonzero temperature using a kind of mean field approximation. To do this let us calculate the impact on an individual at a distance x from the leader of opinion s_L = 1, and sharing the opposite opinion:

Now we make an approximation replacing Pr(r) by its stationary mean value p over D_R and putting it outside the integral. This is equivalent to the simple assumption that Pr(r) is uniform. We can expect it to be valid for large temperatures when the dynamics is almost random, or for small leader's strength s_L (because it is in fact the large value of s_L that contributes most to the nonuniformity of Pr(r)). From (4) we get

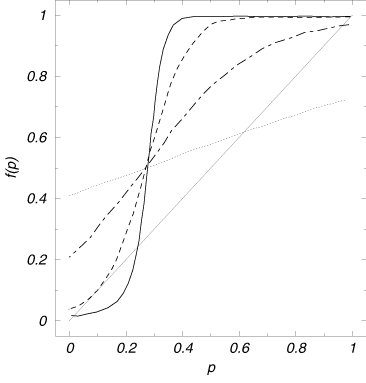
In Fig. 1 one can see the graphical solution of the Eq. (6) for certain set of parameters and g(r) = r. At low temperatures there are three solutions: the smallest one corresponding to the stable cluster around the leader, the second - to the unstable cluster which, in fact, is not observed, and the biggest - to the unification. The size of the stable cluster grows with increasing the temperature up to a critical value T_tr when it coincides with the unstable solution. At this temperature a transition from a stable cluster to unification occurs (Fig. ). For T > T_tr unification is the only solution, but it is no longer a perfect unification because due to the noise individuals of the opposite opinion appear. When the temperature goes on growing the curve in Fig. 1 becomes more flat and p tends to 1/2 what means that the dynamics is random and both opinions appear with equal probability.

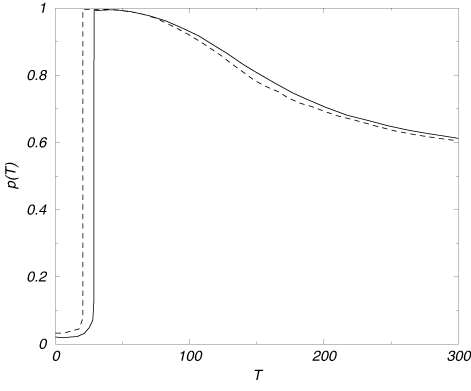
Fig. 2 shows the function p(T) compared with the results of computer simulations. The phase transition mentioned above can be observed. The analytical curve fits the results of simulations quite well, particularly at large temperatures for the reasons mentioned above. Other mean field approximations, e.g. the one used by us in [] yield better results at low noise levels, specifically for the value of the transition temperature. They consist in taking another function (instead of constant) to replace Pr(r) in (4) (e.g. a stepwise in []). In fact, the definition (2) can be used with I given by (5); this would be a ßecond order" extension of our simple approach. Higher order approaches can be constructed in a similar way; they would give more accurate results, however for the price of more complex equation (6) for p.

Let us thus remain at the``first order'' equation (6). Changing the external impact and/or the leader's strength results in a shift of the curves f(p) along the p-axis. If we apply a large enough external impact against (h < 0) the leader the curves f(p) in Fig. 1 would be shifted to the right so that now, starting from the uniform opinion p = 1 and exceeding a critical temperature we observe the transition unification ® cluster which remains the only solution at high noise level.

At a certain value of h = h_b < 0 the influences of the leader and the external impact are in a way balanced and the curve f(p) becomes roughly symmetric with respect to the bisector p. Let us set the condition for the balance as f([1/2]) = [1/2]. With the use of Eqs. (6) and (5) it can be written as

With the increase of temperature at h = h_b (maintained by appropriate changes of s_L) the two stable solutions p₁ and p₂ (corresponding to cluster and unification respectively) converge towards p = [1/2] (the third, unstable solution). At some critical noise level T_c the solutions coincide and we have only p = [1/2] which now becomes stable. The condition for this critical temperature can be written as [(df(p))/(dp)]|_{p = 1/2} = 1. Again using Eqs. (6) and (5) we get an implicit integral equation for T_c:

In the case of g(x) = x we found that the curve f(p) is almost exactly symmetric with respect to the point f([1/2]) and thus p₂ » 1-p₁. Moreover the balanced external impact h_b depends only weakly on the noise level, and the critical temperature T_c is almost independent of the leader's strength s_L.

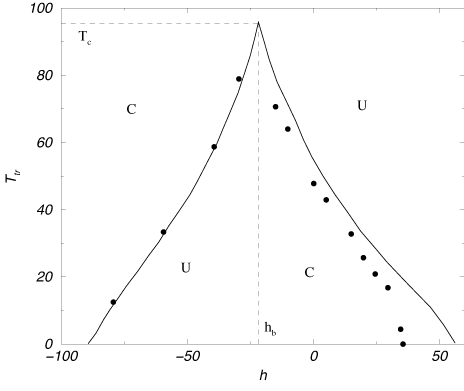
Fig. 3 shows the temperature of the described above transitions cluster ® unification (for h > h_b) and unification ® cluster (for h < h_b) as a function of h. Both curves meet at the critical point h = h_b, T = T_c. When moving along both curves towards the critical point the magnitude of jump in the majority-minority proportion due to transition decreases and at (h_b, T_c) there is no jump at all.

In analogy to physical systems the transitions occurring while crossing the curves in Fig. 3 from below may be called first-order transitions. When the critical point (h_b, T_c), at which the difference between two different phases disappear, is crossed going from the region below the curves a second-order transition occurs. An example of the dynamics in the neighbourhood of this kind of transition is shown in Fig. .

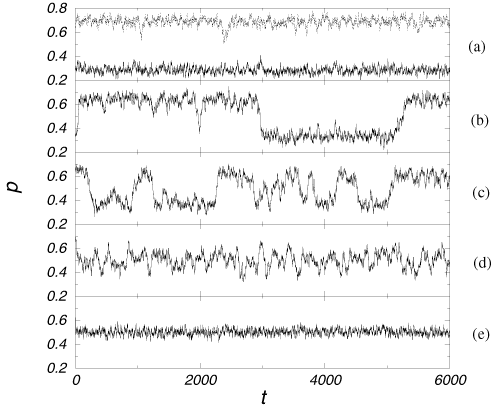
As the solutions p₁ and p₂ are approaching [1/2] increasing fluctuations around them can be observed (Fig. 4 (a)). At T close to T_c, noise induced random jumps between p₁ and p₂ are possible (Fig. 4 (b)). With T ® T_c the average frequency of jumps increases (Fig. 4 (c)), and at T = T_c we observe the dynamics with p = [1/2] and large fluctuations (Fig. 4 (d)). When the temperature is further increased the amplitude of fluctuations decreases (Fig. 4 (e)). Large fluctuations in the vicinity of the critical point are a general characteristic feature of critical phenomena in physical systems.

The described above second-order transition through critical point can also be observed in the absence of a leader and the external impact, i.e. when s_L » [`(s)] and h = 0. Then the two phases corresponding to unifications U+ and U- which are stable in low temperatures merge giving rise to the high temperature phase - at average equal numbers of individuals sharing both opinions. In this case the model reduces to the Ising model with long range interactions if we additionally put s<sub>i</sub> = [`(s)] for every i.

It should also be mentioned that the fluctuations in the vicinity of the critical point are relatively slow, e.g. in our simulations significant changes of p happen during a few tens of time steps. This phenomenon known as the critical slowing down is caused by local correlations of opinions. In the temperatures saliently greater than T_c the correlations disappear and we observe fast random fluctuations around p = [1/2].

The second-order transition occurs also in the opposite direction, i.e. when the temperature is decreased starting from the p = [1/2] phase at T > T_c. At the critical point there is a symmetry breaking; the choice between two symmetric phases depends sensitively on tiny deviations from the balanced external impact h_b and random fluctuations.

One could also describe the global dynamics of the system introducing an effective potential. At low temperatures it would have two minima corresponding to the stable solutions of Eq. (6) separated by a maximum corresponding to the unstable solution. For h = h_b both minima would be approximately equal, but otherwise the one corresponding to the dominance of the stronger agent would be global while the other the local one with the corresponding state being metastable. However, as we have already mentioned, the probability of escape from the metastable state is very small for T < T_tr.

In the analytical calculations of this section we neglected the self supportiveness of individuals putting b = 0. Let us now briefly discuss the effect of a nonzero b. As it was already mentioned, the self support may be regarded as an analogy of dry friction in mechanical systems. It strives to maintain the current state of individuals. Writing the formula (5) for the impact we assumed a stationary state and did not regard how it was achieved. We could do it, as well as to use the formula for the probability in (6) which is independent of the current state only in the case of b = 0. Due to nonzero self support the mean (stationary) value of the proportion p of the leader's adherents depends on the initial state. One can regard that the curve in Fig. 1 splits into a band and so do the appropriate solutions of the Eq. (6). It depends on the starting point on which side of the band the system settles. However, at high temperatures noise induced random walk within the band will finally make the system forget its initial conditions and the mean value for b = 0 will be observed. Accordingly the first order transition occurs when the band looses tangency to the bisector and thus the temperature of transition will be higher than for b = 0. We can also expect that the critical behaviour will be observed in a broader range of temperatures. Nevertheless, for small b (like e.g. b = 1 in our simulations) the influence of the self support is negligible and the results of our mean field theory remain valid.

5  Summary

Let us summarize the outcomes of our analysis. The influence of two agents on the group: the strong leader and an external impact gives rise to multistability in certain ranges of parameters, hysteresis and discontinuous changes in the distribution of opinions in the deterministic case. The situation looks similar in the presence of noise which models the complexity and indeterminism of the process of opinion formation at the level of a particular individual. The noise level (``social temperature'') is an additional transition inducing parameter. We have shown that the noise favours the stronger agent; with growing temperature it needs smaller prevalence to convert the majority to its opinion. In the case of a balance (symmetry) between the two agents the appropriate phase transition becomes continuous and we observe characteristic critical behaviour (large fluctuations, critical slowing down).

The phenomena can be understood and described quantitatively in terms of a mean field approach. In general a hierarchy of approximations can be constructed, but our calculations and computer simulations of the model show that already in the first order we get quite good quantitative results.

The model presented here, though presumably not directly applicable to the description of a real social group, may still be useful in explaining the mechanisms underlying often very complicated social processes. Being aware of their complexity we are circumspectful in drawing far reaching sociological conclusions from our results. Let us point out just one general outcome which seems reasonable: the rapid changes of opinions under the influence of strong leaders and some general preferences or prejudices are more probable during the times of big social transformations or turbulence, when people are much confused in their views (high social temperature). Then the opinion supported by the stronger agent prevails and may remain dominant later on in a more quiet period, even after the influence of the agent decreases or even ceases to exist.

Various modifications and extentions of the model are possible; one of the natural ones is the introduction of more than one leaders. A motivating question, also relevant to real life problems, is how to distribute efforts (money, investments, human resources) in order to convince a unified group of people to a given opinion; is it more efficient to concentrate them in one place (one strong leader) or rather to disperse them (a few weaker leaders), if so, in how many parts? These problems will be the subject for future studies.

References

 

[]

H. Haken, Synergetics. An Introduction, Springer-Verlag, Heidelberg, New York, 1983; Advanced Synergetics, Springer-Verlag, Heidelberg, New York, 1983.

 

[]

G. A. Cowan, D. Pines, D. Meltzer (eds.), Complexity. Metaphors, Models, and Reality, Addison-Wesley, Santa Fe, 1994.

 

[]

D. Amit, Modeling Brain Function, Cambridge Univ. Press, Cambridge, 1989; E. Domany, J.L. van Hemmen, K. Schulten (eds.) Models of Neural Networks, Springer, Berlin, 1995; A. Browne (ed.), Neural network analysis, architectures and applications, Institute of Physics Publishing, Bristol, 1997.

 

[]

A. Johansen, Physica D 78 (1994) 186; H. C. Tuckwell, L. Toubiana, J-F. Vibert, Phys. Rev. E. 57 (1998) 2163.

 

[]

P. Bak, K. Sneppen, Phys. Rev. Lett. 71 (1993) 4083. A. Pekalski, Physica A 252 (1998) 325;

 

[]

D. Helbing, Phys. Rev. E 55 (1997) 3735; Physica A 219, (1995) 375; D. Helbing, P. Molnar, Phys. Rev. E 51 (1995) 4282.

 

[]

W. Weidlich, G. Haag, Concepts and Models of Quantitatively Sociology, Springer, Berlin, New York, 1983; W. Weidlich, Physics Reports 204 (1991) 1;

 

[]

J. Fort, V. Méndez, Phys. Rev. Lett. 82 (1999) 867.

 

[]

D. Sornette, A. Johansen, Physica A 245 (1997) 1; N. Vandewalle, M. Ausloos, P. Boveroux, A. Minguet, Eur. Phys. J. B 4 (1998) 139.

 

[]

W. Weidlich, J. Math. Sociology 18 (1994) 267.

 

[]

D. Helbing, Physica A 193 (1993) 241; J. Math. Sociology 19 (1994) 189; D. Helbing, Quantitative Sociodynamics, Kluwer Academic, Dordrecht, 1995.

 

[]

S. Galam, Physica A 230 (1996) 174; 238 (1997) 66.

 

[]

D. B. Bahr, E. Passerini, J. Math. Sociology 23 (1998) 1;29.

 

[]

S. Wolfram, Theory and Application of Cellular Automata, World Scientific, Singapore, 1986; H. Gutowitz (ed.), Cellular automata, theory and experiment, MIT Press, London, 1991.

 

[]

B. Latané, Am. Psychologist 36 (1981) 343.

 

[]

R. R. Vallacher, A. Nowak (Eds.), Dynamical systems in social psychology, San Diego, Academic Press, 1994.

 

[]

E. L. Fink, J. Communication 46 (1996) 4; B. Latané, J. Communication 46 (1996) 13.

 

[]

A. Nowak, J. Szamrej, B. Latané, Psych. Rev. 97 (1990) 362.

 

[]

M. Lewenstein, A. Nowak, B. Latan\'e , Phys. Rev. A 45 (1992) 763.

 

[]

D. Plewczy\'nski, Physica A 261 (1998) 608.

 

[]

G. A. Kohring, J. Phys. I France 6 (1996) 301.

 

[]

K. Kacperski, J.A. Ho yst, J. Stat. Phys. 84 (1996) 169.

 

[]

K. Kacperski, J.A. Ho yst, Leaders and clusters in a social impact model of opinion formation: the case of external impact, in: F. Schweitzer (ed.) Self-Organization of Complex Structures: From Individual to Collective Dynamics, Vol II, Gordon and Breach, Amsterdam 1997.

 

[]

K. Kacperski, J.A. Ho yst, Physica A 269 (1999) 511.

 

Footnotes:

¹e-mail: kacper@mpipks-dersden.mpg.de

²e-mail: jholyst@if.pw.edu.pl