DRGANIA WYMUSZONE
Równanie różniczkowe
drgań wymuszonych. Rezonans.
* Równanie różniczkowe drgań wymuszonych
* Amplituda drgań wymuszonych. Rezonans

Do układu mogącego wykonywać
drgania tłumione przykładamy siłę zewnętrzną zmieniającą się harmonicznie z
częstotliwością kątową Ω, czyli siłę Fx = F0 cos
Ωt.

Należy zauważyć, że siłę przykładamy w sposób „miękki”,
poprzez sprężynę tak, że układ może poddawać się w różny sposób wpływowi siły
wymuszającej. W drganiach wymuszonych
amplituda, a zatem i energia przenoszona do układu drgającego zależy od różnicy
między częstotliwością Ω siły zewnętrznej a częstotliwością ω0
drgań swobodnych układu jak również od wielkości tłumienia. Ponieważ siła
zewnętrzna jest cosinusoidalna i jest być zadana przez równanie
![]()
to równanie drgań ma postać
![]()
albo
![]() (1)
(1)
![]()
Równanie (1) jest niejednorodnym równaniem różniczkowym
drugiego rzędu o stałych współczynnikach. Rozwiązanie ogólne tego równania niejednorodnego jest sumą
rozwiązania ogólnego równania jednorodnego i jakiegokolwiek rozwiązania
szczególnego równania niejednorodnego.
![]()
Rozwiązanie ogólne równania
jednorodnego jest przypadkiem drgania tłumionego i ma znaną nam już postać
![]()
Szukamy teraz rozwiązania szczególnego równania
niejednorodnego. Zastosujemy następujący chwyt: do prawej strony równania (1)
dodajemy chwilowo człon if0 sin(Ωt), stosujemy wzór Eulera i
otrzymujemy prawą stronę w postaci wykładniczej, w rezultacie czego otrzymujemy
![]()
Poszukujemy rozwiązania szczególnego w postaci
![]()
Zatem
![]()
Podstawiamy te wyrażenia do (1) i otrzymujemy
![]()
Rozwiązanie zostanie otrzymane, jeżeli znajdziemy amplitudę zespoloną ![]() , którą wyrazimy z powyższego równania
, którą wyrazimy z powyższego równania
![]()
Mianownik tego wyrażenia możemy zapisać jako
![]()
Zatem amplituda ma postać
![]()
Wracamy teraz do części rzeczywistej (zwracamy pożyczoną
część urojoną) i otrzymujemy ostateczną postać rozwiązania szczególnego
![]()
lub po prostu
![]()
Poszukiwanym rozwiązaniem ogólnym równania (1) jest zatem
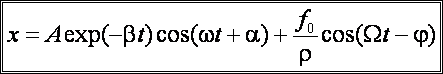
Lewy człon sumy ma znaczenie jedynie w początkowej fazie
ruchu dlatego że czynnik e-βt powoduje zanik tego członu z
upływem czasu.
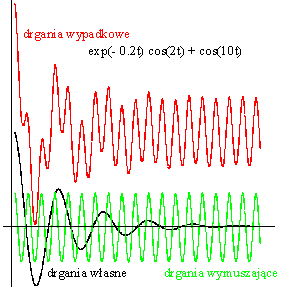
Na wykresie poniżej przedstawiono
drgania gasnące układu, w którym nie będzie występowała siła wymuszająca (kolor
czarny), drgania wymuszające (kolor zielony) i drgania wymuszone układu (kolor
czerwony). Zgodnie z rozwiązaniem przedstawionym wyżej, drgania wymuszone, po
początkowym chaotycznym okresie drgań nieustalonych, będą odbywały się w takt
„miękkiej” siły wymuszającej.


Z rozwiązania szczególnego
równania niejednorodnego widzimy, że amplituda drgań wymuszonych - po ustaleniu
się tych drgań - zależy od częstotliwości drgań wymuszających Ω i od
współczynnika tłumienia β:
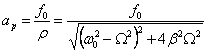
Przy pewnych
wartościach częstotliwości drgań wymuszających Ω wzrost amplitudy drgań
jest szczególnie duży i zjawisko to nazywamy rezonansem. Rezonans ma często kluczowe znaczenie w wielu dziedzinach
nauki i techniki. Może on być zjawiskiem bardzo pożytecznym, jak w brzmieniu
instrumentów muzycznych czy w magnetycznym rezonansie jądrowym, stosowanym
także w medycynie. Może też prowadzić do katastrofalnych następstw, kiedy
wystąpi w konstrukcjach budowlanych czy w samolotach. Znajdowanie amplitudy
rezonansowej jest zwykłym poszukiwaniem maksimum funkcji, czyli przyrównanie do
zera pochodnej. Ponieważ amplituda ![]() jest funkcją Ω
typu
jest funkcją Ω
typu
![]()
to pochodnej poszukujemy wg reguły
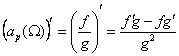
Otrzymujemy
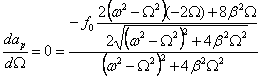
czyli
![]()
Pierwiastkami tego równania są
![]()
oraz
![]()
Ponieważ ujemna częstotliwość nie ma sensu, wybieramy jako
częstotliwość rezonansową wartość
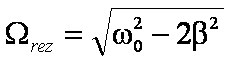
Uwaga: Porównaj z częstotliwością drgań tłumionych
![]()
Po podstawieniu częstotliwości rezonansowej Ωrez w miejsce Ω w równaniu na amplitudę drgań wymuszonych
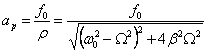
otrzymujemy wyrażenie
na amplitudę rezonansową:
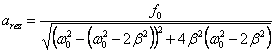
czyli
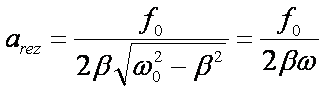
Dla wartości β małych w porównaniu z ω0
amplituda rezonansowa jest
![]()
Dla 2β2 > ω02
częstotliwość rezonansowa jest urojona.
Zjawisko
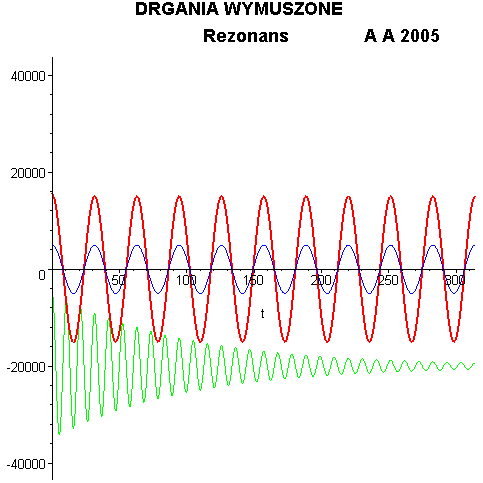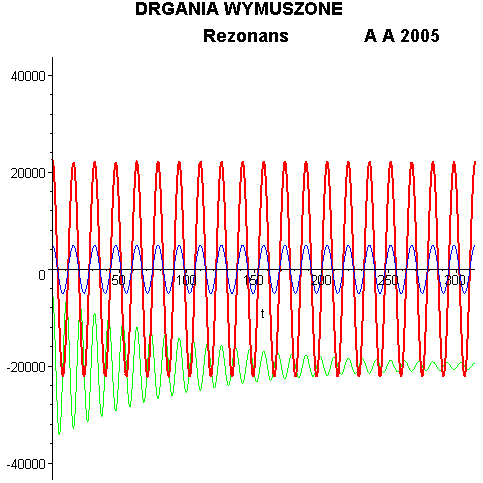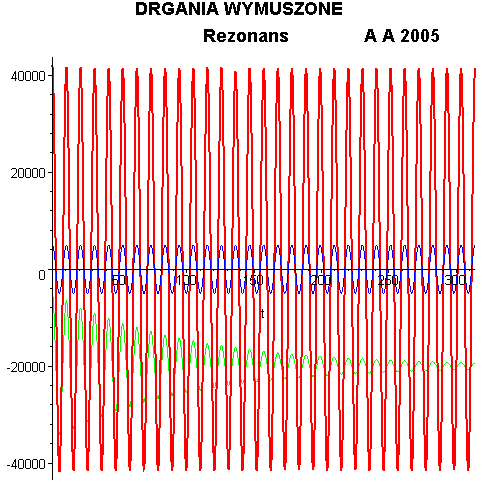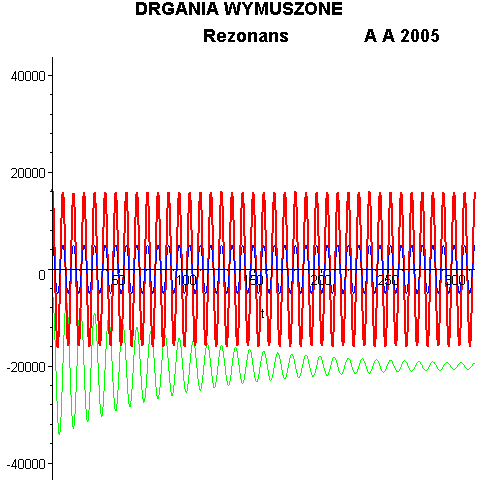
rezonansu jest zobrazowane w animacji poniżej. Jeżeli układ, który bez
wymuszenia wykonywałby zwykłe drgania gasnące (zielony przebieg) zostanie
poddany sile wymuszającej o zmieniającej się częstotliwości (niebieski
przebieg) to w miarę zbliżania się do częstotliwości rezonansowej odpowiedź
układu (czerwony przebieg) gwałtownie wzrasta.
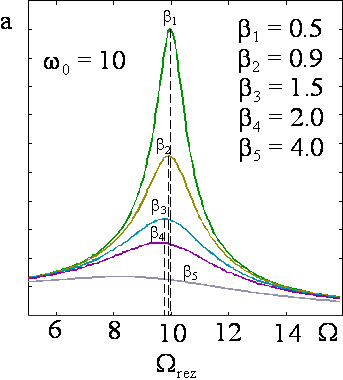
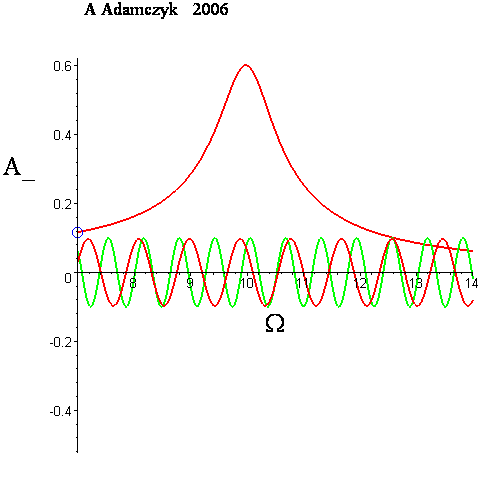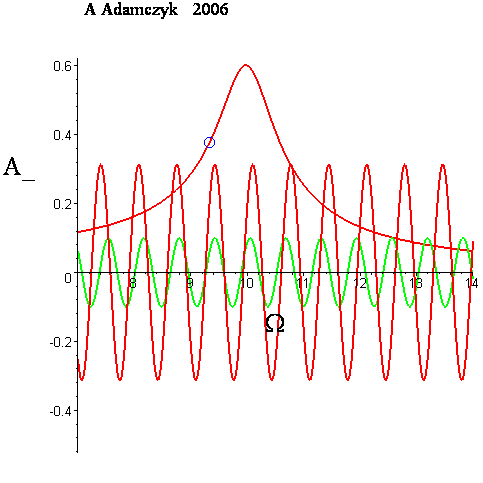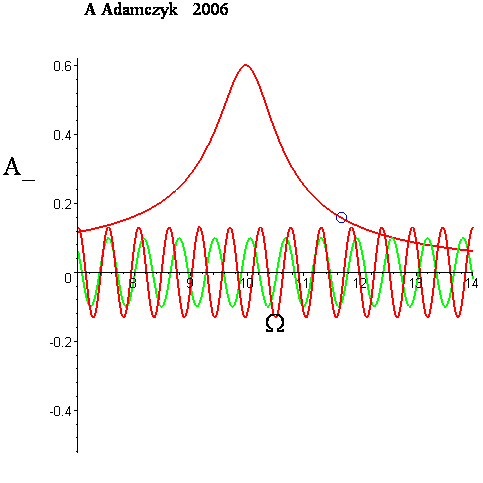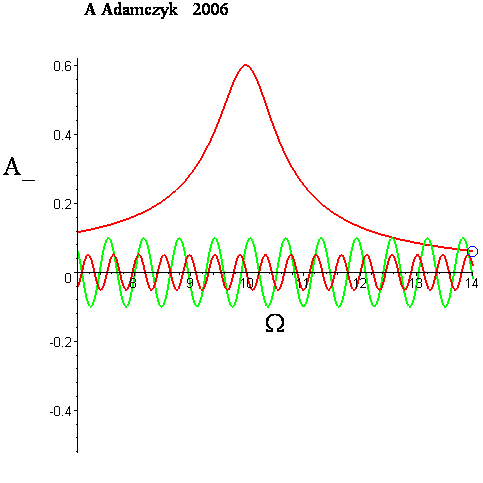
Kształt krzywej rezonansowej, czyli zależności amplitudy A od częstotliwości wymuszającej Ω, jest przedstawiony na animacji poniżej. Aktualna wartość Ω jest zaznaczona na krzywej rezonansowej przez poruszające się kółeczko.
Wraz ze wzrostem współczynnika tłumienia β gwałtownie spada wartość amplitudy rezonansowej a jednocześnie zmniejsza się wartość częstotliwości rezonansowej Ωrez.