SKŁADANIE
DRGAŃ HARMONICZNYCH
Rozkład
drgań nieharmonicznych na szeregi Fouriera. Analiza harmoniczna.

Składanie drgań równoległych ma
również inne, niezwykle ważne, zastosowania w nauce i technice. Problem leży w
tym, że wiele obserwowanych lub celowo generowanych drgań ma charakter bardziej
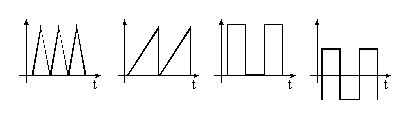
złożony niż drgania harmoniczne. Drgania, których kształty nie są opisywane
sinusoidą lub cosinusoidą, jak np. drgania trójkątne, piłokształtne,
prostokątne itd., nie są drganiami harmonicznymi
Istnieje
jednak wspaniała technika, zwana analizą harmoniczną (lub analizą Fouriera),
która pozwala drgania okresowe o dowolnym kształcie przedstawić jako sumę drgań
harmonicznych. Technika ta polega na rozkładaniu analizowanego drgania
okresowego na drgania harmoniczne, czyli na przedstawianiu okresowej funkcji
czasu f(t) jako sumy nieskończonego szeregu trygonometrycznego, którego wyrazy
są funkcjami albo tylko sinus lub tylko cosinus. W praktyce szereg
„nieskończony” składa się z nie więcej niż z 20-30 wyrazów.
Podstawowa cecha tych szeregów jest taka, że jeżeli funkcja f(t) zmienia się
okresowo z okresem T, to pierwszy wyraz szeregu ma częstotliwość ![]() , zwaną częstotliwością podstawową, a następne mają
częstotliwości harmoniczne, tzn. będące całkowitymi wielokrotnościami
częstotliwości podstawowej, czyli 2ω, 3ω, 4ω ... Żadne z tych
drgań nie może mieć częstotliwości mniejszej od ω ani
częstotliwości nie będącej całkowitą wielokrotnością ω , np.
nie może być 3.5 ω . Widać więc, że okres drgań T =
2π/ω odpowiadający częstotliwości podstawowej ω jest najdłuższym okresem jakie mogą mieć
składowe Fouriera. Poniżej przedstawiono obraz rozkładu drgania złożonego na
składowe Fouriera.
, zwaną częstotliwością podstawową, a następne mają
częstotliwości harmoniczne, tzn. będące całkowitymi wielokrotnościami
częstotliwości podstawowej, czyli 2ω, 3ω, 4ω ... Żadne z tych
drgań nie może mieć częstotliwości mniejszej od ω ani
częstotliwości nie będącej całkowitą wielokrotnością ω , np.
nie może być 3.5 ω . Widać więc, że okres drgań T =
2π/ω odpowiadający częstotliwości podstawowej ω jest najdłuższym okresem jakie mogą mieć
składowe Fouriera. Poniżej przedstawiono obraz rozkładu drgania złożonego na
składowe Fouriera.
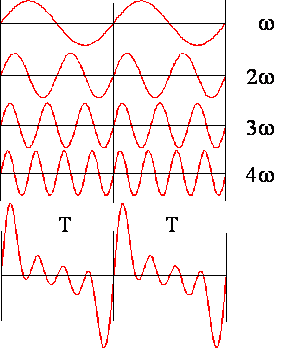
Tworzenie się drgania piłokształtnego jako sumy wyrazów szeregu Fouriera jest przedstawione w animacji poniżej:
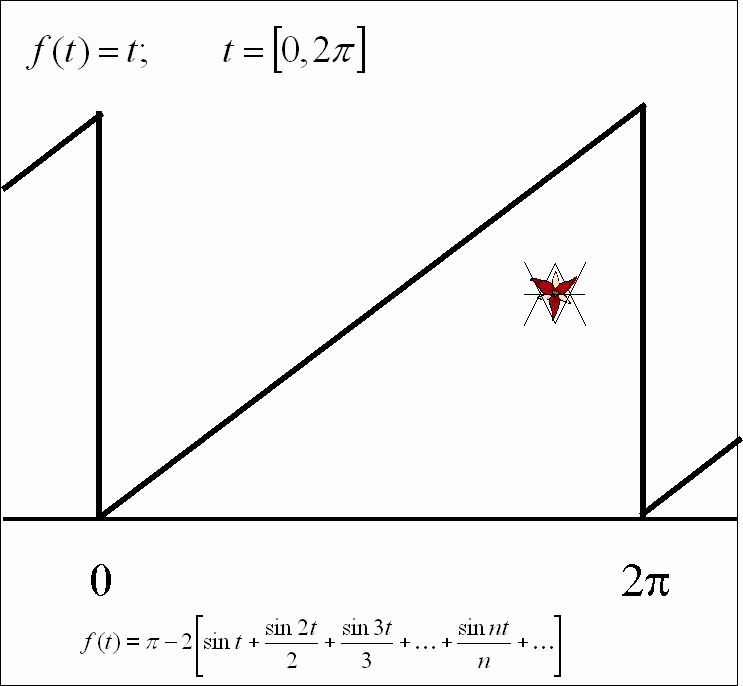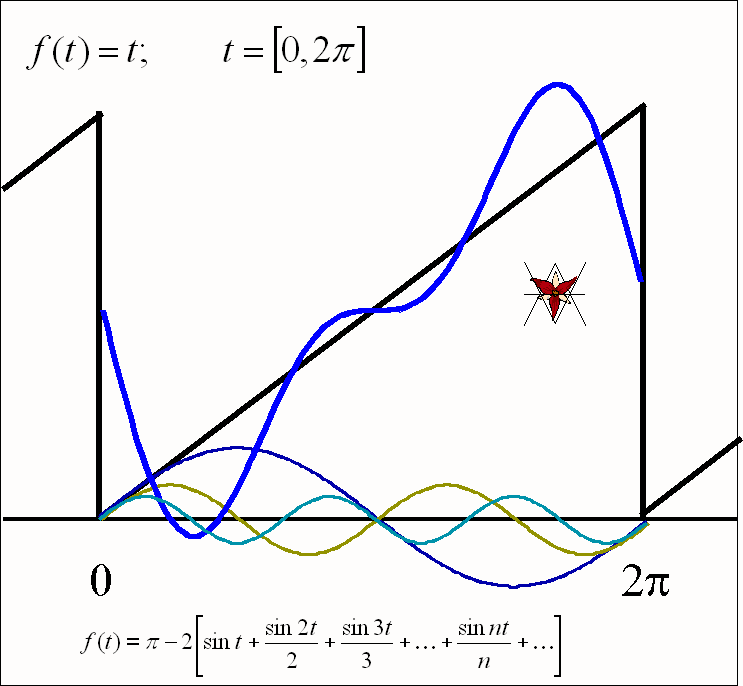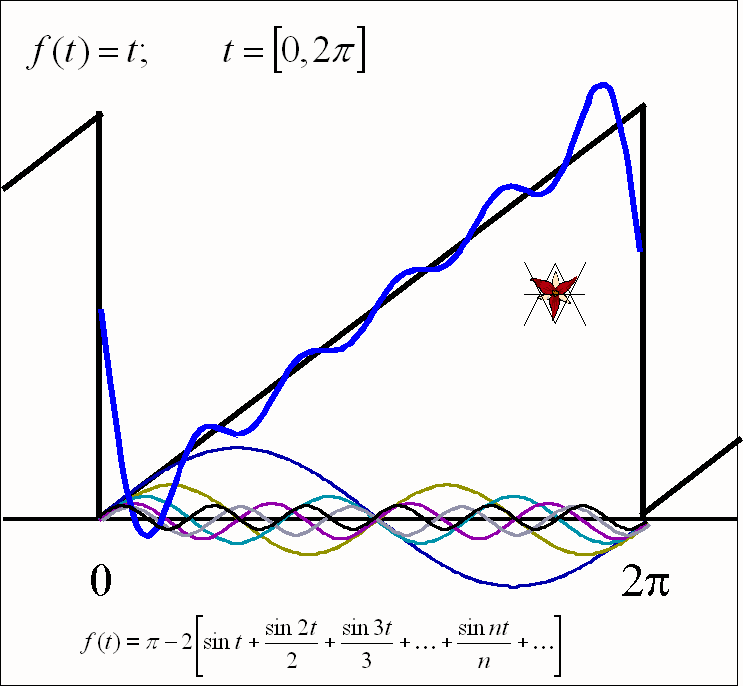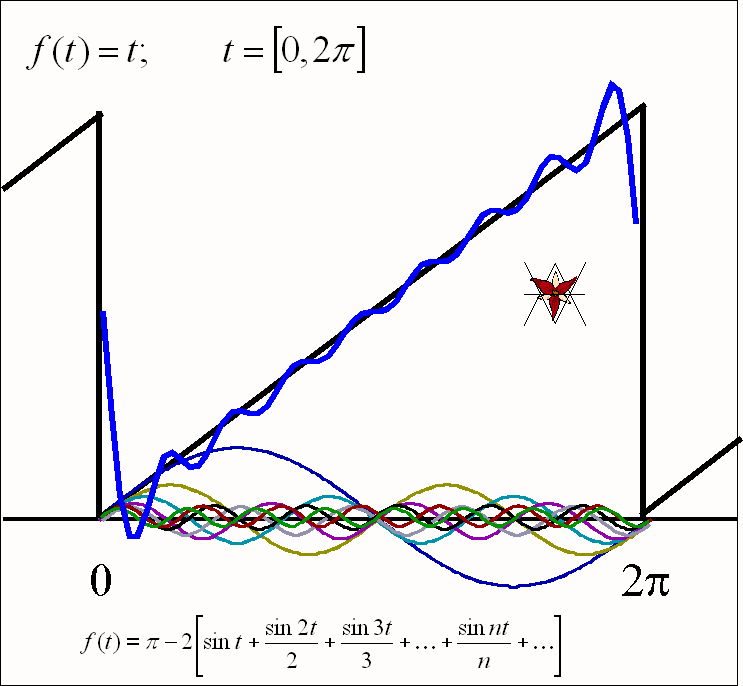
Szereg Fouriera ma następującą postać:
 (1)
(1)
gdzie współczynniki a0, an i bn noszą nazwę współczynników Fouriera:
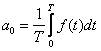
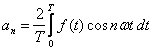
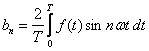
Widać zatem, że rozkład określonego
drgania w szereg Fouriera sprowadza się w rzeczywistości jedynie do znalezienia
współczynników Fouriera wg powyższych równań.
Równania określające współczynniki
Fouriera zostały znalezione w oparciu o wspaniałą własność funkcji
trygonometrycznych zwaną ortogonalnością. Mówimy, że dwie funkcje są
ortogonalne względem siebie, gdy całka z ich iloczynu, wzięta po całym okresie
zmienności tego iloczynu, jest równa zeru. Oznacza to, że dla całkowitych m i n jeśli m jest różne od n to są
spełnione równania
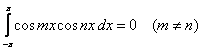
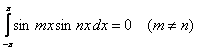
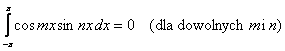
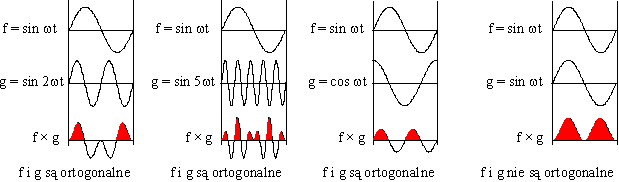
Granice całkowania mogą być inne pod warunkiem, że przedział całkowania będzie miał długość odpowiadającą okresowi 2π. Geometrycznie ortogonalność oznacza, że dla krzywej iloczynu dwóch funkcji ortogonalnych powierzchnia nad osią układu jest równa powierzchni pod osią. Na rysunku poniżej przedstawiono ortogonalność funkcji sin ωt i sin 2ωt, sin ωt i sin 5ωt oraz sin ωt i cos ωt. Funkcja sin ωt nie jest ortogonalna względem samej siebie.
Szukając n-tego współczynnika,
obie strony równania (1) mnożymy przez cos(nωt) dla współczynnika an
lub przez sin(nωt) dla współczynnika bn. Następnie wyliczamy
wartości średnie obu stron równania w całym okresie zmienności [0, T]:
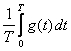
W przedziale [0, T] wartość średnia funkcji cos(nωt) i
sin(nωt) jest, oczywiście, równa zeru. Iloczyny funkcji trygonometrycznych
zamieniamy wg reguł:
![]()
![]()
![]()
A zatem, wartości średnie iloczynów będą następujące:
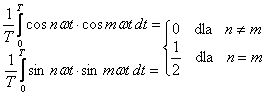
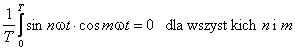
Teraz łatwo znajdujemy współczynniki an i bn:
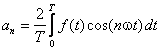

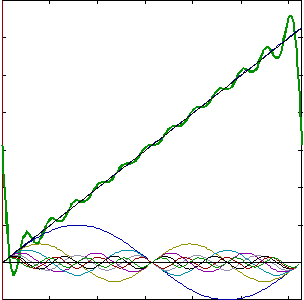
Jeżeli, na przykład, szukamy współczynnika a4,
mnożymy obie strony równania (1) przez cos4ωt i otrzymujemy
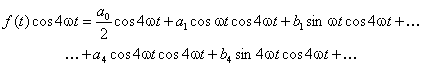
Piszemy wyrażenie na wartość średnią w przedziale [0, T]
obu stron otrzymanego równania
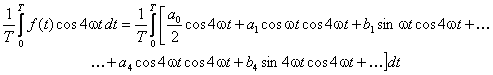
Po zastosowaniu relacji ortogonalności znajdujemy, że jedynym niezerowym
wyrazem po prawej stronie będzie
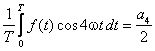
Stąd
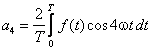
Przykłady rozwinięć w szeregi Fouriera
kilku funkcji okresowych oraz graficzne zaprezentowanie wyrazów szeregu i ich
sumy:
- Drgania
piłokształtne f(t) = t w przedziale [0, 2B]:
![]()
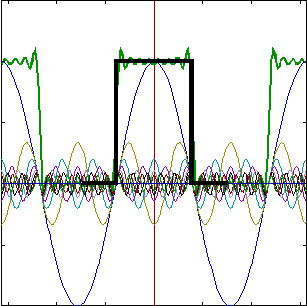
2. Drgania prostokątne 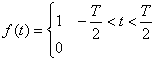 o okresie T:
o okresie T:
![]()
3. Drgania paraboliczne f(t) = t2 w
przedziale [ -π, π]:
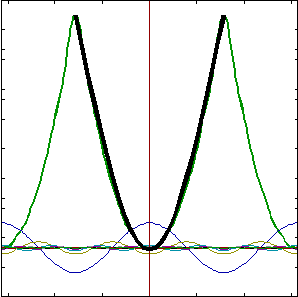
![]()
4. Parabola f(t) = t2 w przedziale [0, 2π]:
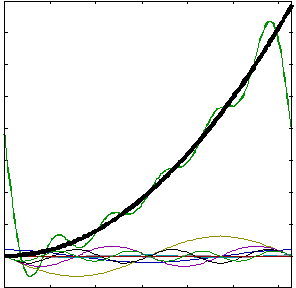
![]()
5. Drgania prostokątne ![]()
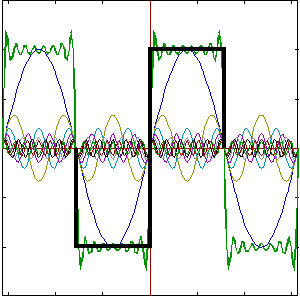
![]()


Wzór Eulera jest znakomitym
narzędziem także w analizie harmonicznej, czyli w analizie zawartości drgań
harmonicznych w badanym okresowym drganiu nieharmonicznym.
Jeżeli do szeregu Fouriera (1)
![]()
ze współczynnikami Fouriera
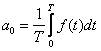
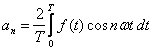
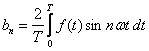
zastosujemy wzór Eulera,
![]()
![]()
wtedy funkcje trygonometryczne z szeregu (1) otrzymamy w postaci
![]()
![]()
Po podstawieniu tych wyrażeń do równania (1) otrzymujemy
![]()
oraz
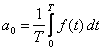
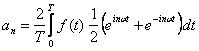
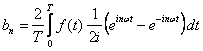
Te wyrażenia łatwo przekształcamy do postaci
![]()
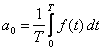
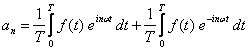
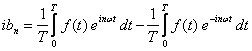
Możemy teraz zdefiniować nowe współczynniki
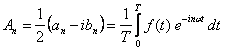
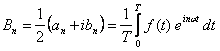
a wtedy szereg Fouriera otrzymujemy w postaci
![]()
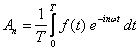
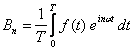
Kiedy następnie zmienimy granice sumowania z (1, ∞) na (-∞, ∞) to zniknie nam wyraz a0 a sam szereg Fouriera będziemy mogli zapisać w postaci bardzo prostej z jednym tylko współczynnikiem cn:
 (2)
(2)
Współczynnik cn wyraża się wzorem
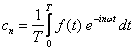
Relacja ortogonalności jest teraz także bardzo prosta:
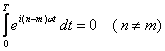
Zaletą
przedstawienia szeregu Fouriera w postaci zespolonej jest możliwość scharakteryzowania
drgania nieharmonicznego za pomocą jednego tylko widma. Rzeczywiście,
równanie (2)
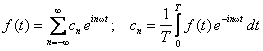
może być w prosty sposób
zilustrowane przez widmo częstotliwości utworzone przez ciąg odcinków
prostopadłych do osi czasu t, z których każdy obrazuje wartość i znak każdej
n-tej składowej harmonicznej:
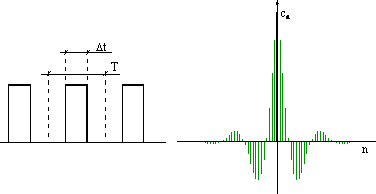
Widmo częstotliwości zmienia się w miarę zmian gęstości
impulsów (stopnia wypełnienia) gdzie Δt czasem trwania impulsu a T jest
okresem jego powtarzania się. Im stopień wypełnienia impulsu jest mniejszy
(impulsy stają się coraz krótsze w stosunku do długości całego okresu) tym
gęściej ustawione są odcinki tworzące widmo:
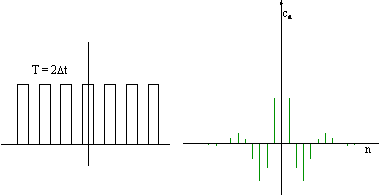
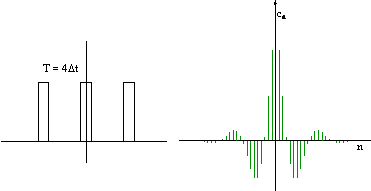
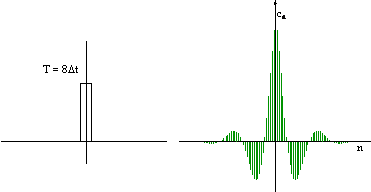
Widmo częstotliwości pozwala jednym rzutem oka ocenić zawartość harmonicznych w konkretnym analizowanym przebiegu okresowym.