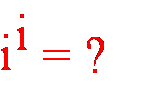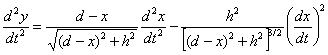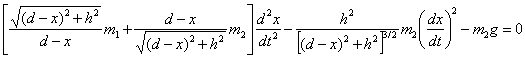WSTĘP DO
ANALIZY DRGAŃ HARMONICZNYCH
Liczby
zespolone. Równania różniczkowe.
* Postać algebraiczna i postać trygonometryczna liczby zespolonej
* Wzór Eulera i postać wykładnicza liczby zespolonej
* Operacje algebraiczne na liczbach zespolonych
* Zastosowanie wzoru Eulera do otrzymywania wzorów na funkcje trygonometryczne sum i różnic kątów
* Równania różniczkowe zwyczajne o stałych współczynnikach
* Równania I-go rzędu: Przypadek zmiennych separowalnych
* Równania II-go rzędu o stałych współczynnikach
* Nieliniowe równania różniczkowe
Drganiami harmonicznymi w mechanice nazywamy proste drgania okresowe, w których wychylenie jest opisywane funkcjami sinus lub cosinus. Ciało wykonujące takie drgania powinno spełniać dwa warunki:
1. musi mieć masę aby siłą bezwładności powrócić do stanu początkowego oraz
2. musi na to ciało działać siła zwrotna skierowana przeciwnie do kierunku odchylenia od stanu równowagi.
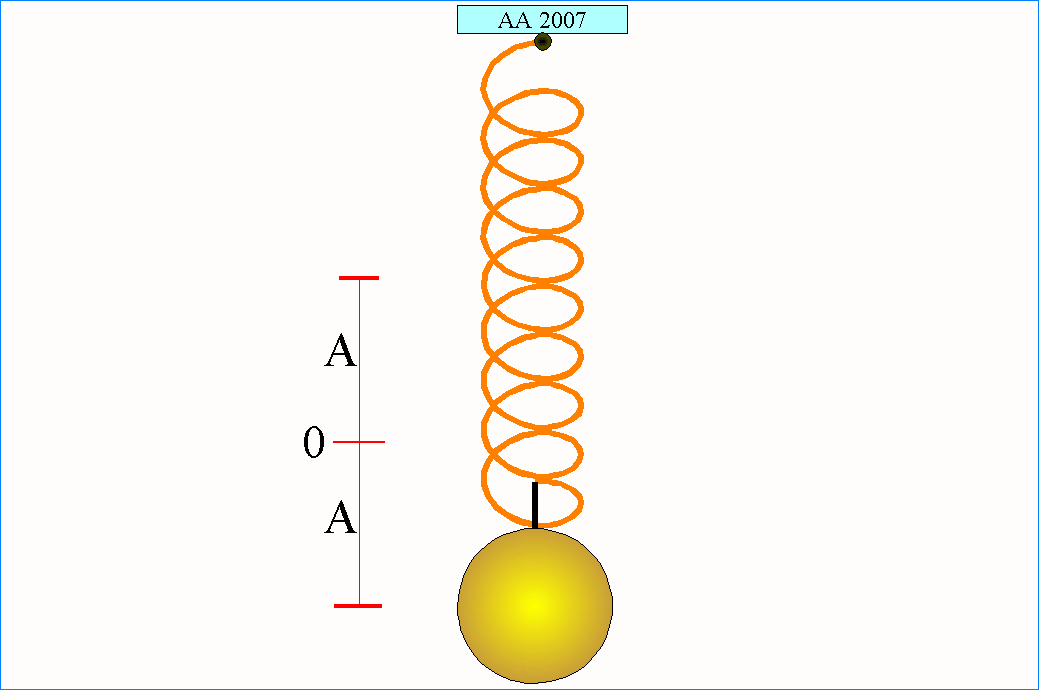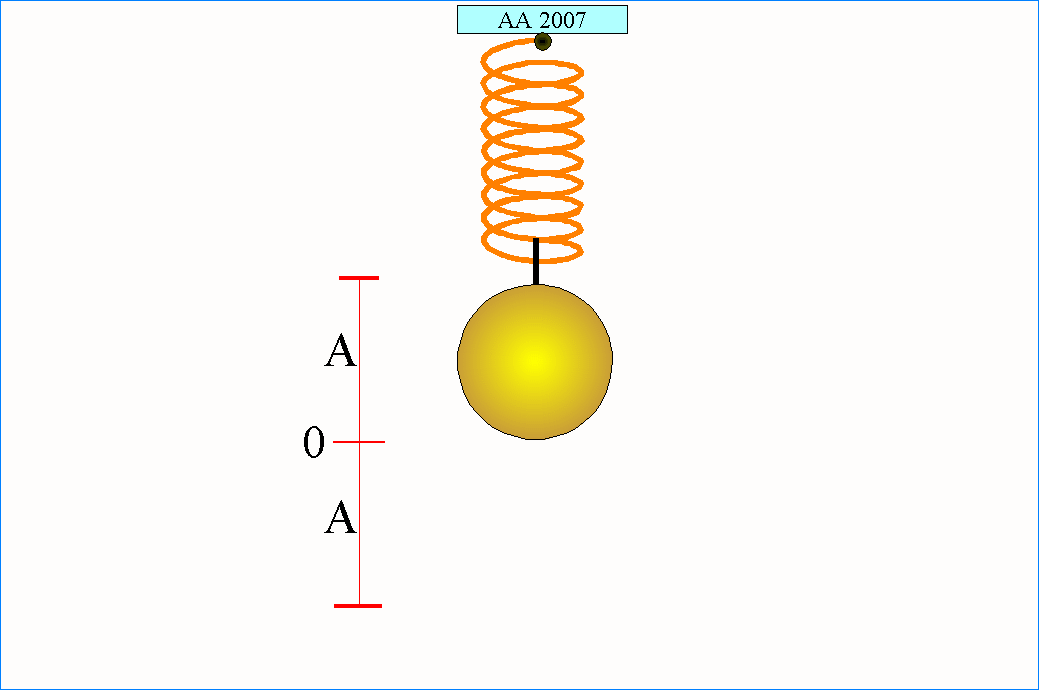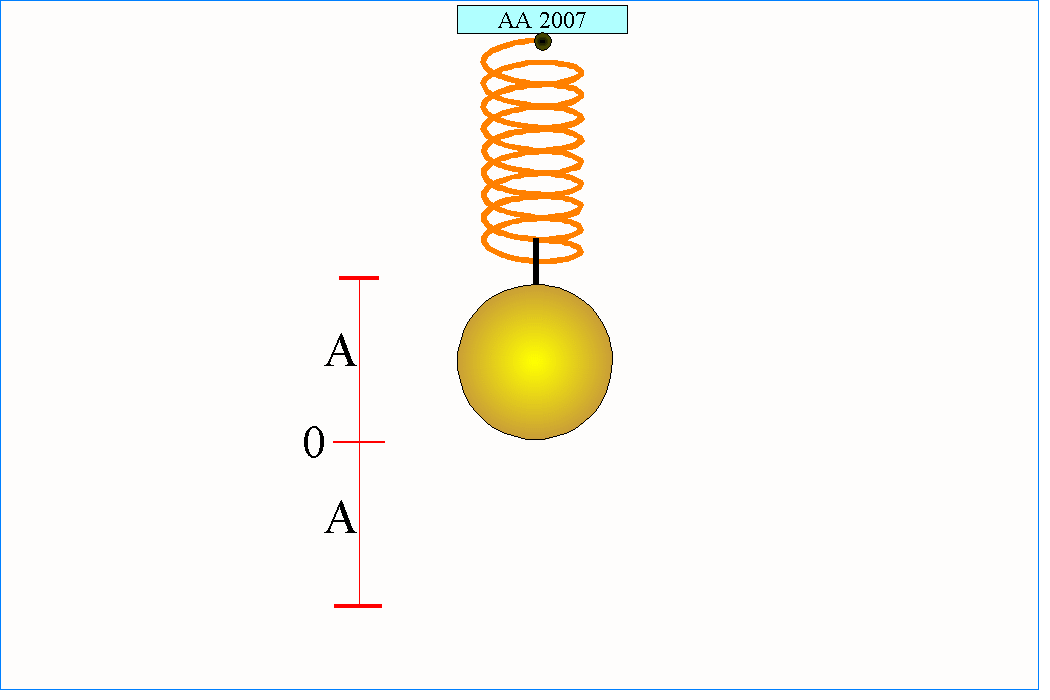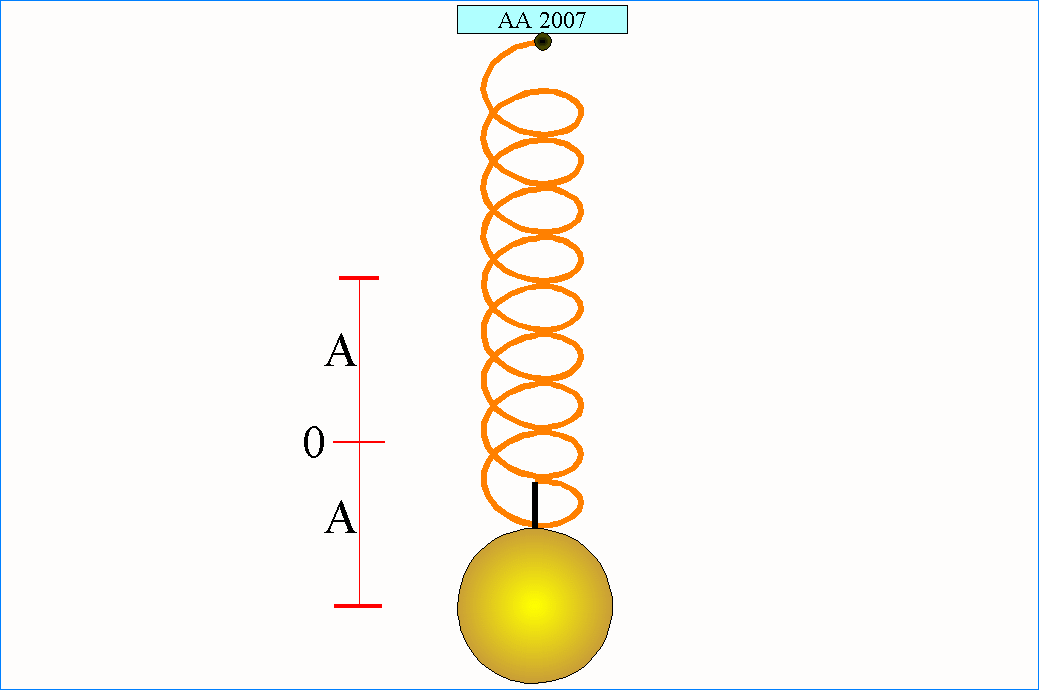
Proste drgania harmoniczne pojawia się w układzie złożonym z kulki o masie m przymocowanej do idealnej nieważkiej sprężyny. Stalowa kulka znajdująca się wewnątrz szkiełka zegarkowego też może wykonywać drgania w przybliżeniu harmoniczne, jeżeli zostanie wstępnie lekko poruszona. Ta sama kulka położona na wierzchołku odwróconego szkiełka zegarkowego po prostu z niego spadnie, ponieważ nie będzie w tym przypadku spełniony drugi z warunków (tym razem siła działająca na kulkę będzie zgodna z jej wychyleniem).



Dotychczas znane nam liczby
całkowite, wymierne i niewymierne nazywamy liczbami rzeczywistymi i każdą z
nich można przedstawić jako punkt na odpowiedniej osi liczbowej. Kiedy jednak
liczba ma reprezentować pewną wartość złożoną z dwóch różnych wielkości, to
taka liczba reprezentuje już punkt na specjalnej płaszczyźnie? Na przykład
liczba „majątek” może składać się ze zmiennej „domy” i
zmiennej „samochody”.
Wtedy: majątek = domy +
samochody.
Aby na takich liczbach można było przeprowadzać operacje
dodawania, odejmowania, mnożenia i dzielenia, to jedną ze składowych należy
jakoś wyróżnić (np. zakolorować).
Jeżeli analizujemy dwie grupy ludzi z1 i z2,
to może być istotne ile każda z tych grup zawiera mężczyzn i ile kobiet.
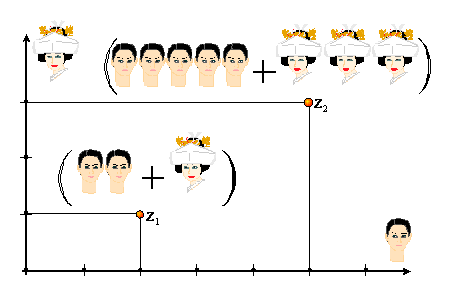
Obie grupy przedstawiliśmy na
płaszczyźnie, na której jedna z osi reprezentuje mężczyzn, a druga z osi
– kobiety. Pewnym uproszczeniem byłoby zastosowanie liczb oznaczających
mężczyzn i oddzielnie kobiety:
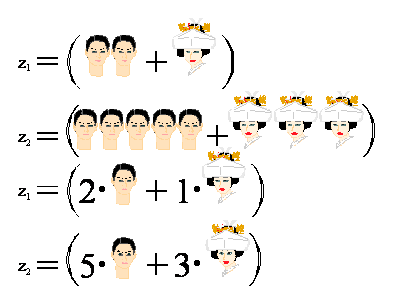
Ciągle jednak nie uniknęliśmy
malowania symboli twarzy. Genialnym pomysłem było zastosowanie liczby urojonej
„i”:
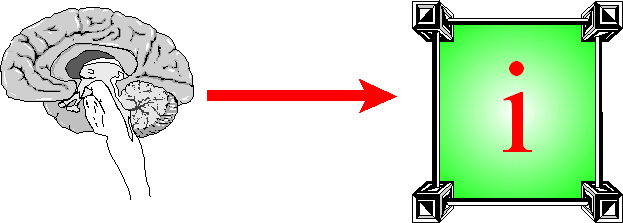
która posłuży do „zakolorowania” liczby oznaczającej
kobiety, co pozwoli nam na radykalne uproszczenie zapisu. Naga liczba będzie
teraz oznaczała mężczyzn, zakolorowana – kobiety:

Liczba „i” jest jednostką urojoną i każda liczba zakolorowana tą jednostką staje się liczbą urojoną. Liczba będąca sumą liczb rzeczywistej i urojonej nosi nazwę liczby zespolonej i jest tradycyjnie oznaczana literą z.
Np. w liczbie z = 10 + 3i liczba 10 jest częścią rzeczywistą liczby z, oznaczaną przez Re z (od realis), a liczba 3i jest częścią urojoną liczby z, oznaczaną przez Im z (od imaginarius). Nazwa ‘urojona’ jednostki „i” pochodzi z jej określenia jako pierwiastka kwadratowego z „-1”:
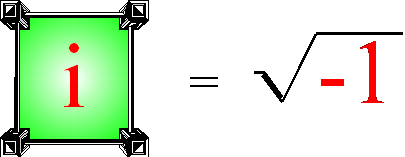
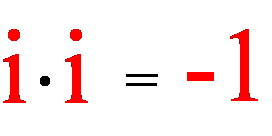
Liczbą zespoloną nazywamy zatem liczbę o postaci
![]()
gdzie x i y są liczbami rzeczywistymi; liczbę x nazywamy częścią
rzeczywistą liczby zespolonej, Re z, zaś liczbę y - jej częścią urojoną, Im z.
Liczba
![]()
jest nazywana liczbą sprzężoną do liczby z. Łatwo zauważyć, że
![]()
Liczby zespolone mają prostą interpretację geometryczną. Liczbę zespoloną
z = x + iy traktujemy jako punkt na pewnej płaszczyźnie.
Płaszczyzna, której jedna z osi układu określa wartości urojone a druga
oś – wartości rzeczywiste, jest nazywana płaszczyzną zespoloną lub
płaszczyzną Arganda:
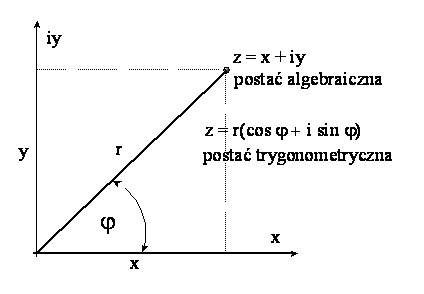
Każdy punkt na tej
płaszczyźnie oznacza jedna liczbę zespoloną. Promień r łączący początek
układu z liczbą z nazywamy modułem liczby z. Moduł r reprezentuje
bezwzględną wartość liczby zespolonej
![]()
Kąt φ między osią z, a promieniem r nazywamy argumentem liczby z.
Postać liczby zespolonej z = x + iy nosi nazwę postaci
algebraicznej. Liczbę zespoloną można także przedstawić w postaci trygonometrycznej (we współrzędnych
biegunowych) korzystając z jej modułu i argumentu. Ponieważ x = r cos φ
oraz y = r sin φ, to każdą liczbę zespoloną można przedstawić w dwóch
równoważnych postaciach: algebraicznej i trygonometrycznej
![]()
Dwie liczby zespolone z1
= x1 + i y1 oraz z2 = x2 + i y2
są równe wtedy, gdy ich moduły są równe, r1 = r2, a ich
argumenty mogą się różnić tylko o całkowitą wielokrotność 2π:
![]()

Wspaniałą i
niezwykle użyteczną relacją między funkcjami trygonometrycznymi i wykładniczymi
w dziedzinie zespolonej jest wzór Eulera:

![]()
Stosując wzór Eulera automatycznie otrzymujemy postać wykładniczą liczby zespolonej
![]()
![]()
![]()

Dodawanie (odejmowanie) liczb zespolonych: Liczby zespolone dodajemy do siebie w ten sposób, że
oddzielnie dodajemy części rzeczywiste i oddzielnie urojone. Odejmowanie
przeprowadzamy analogicznie.
Mnożenie, dzielenie i potęgowanie liczb zespolonych w postaci trygonometrycznej:
![]()
![]()
Mnożąc wielokrotnie tę samą liczbę przez siebie otrzymujemy
potęgę liczby zespolonej (tzw. wzór de
Moivre'a):
![]()
Przez zastosowanie postaci wykładniczej liczb zespolonych
operacje mnożenia i dzielenia tych liczb stają się dziecinnie proste
![]()
![]()
Mnożąc liczbę z przez sprzężoną do niej z* otrzymujemy zawsze kwadrat modułu liczby r2 niezależnie od postaci liczby z (algebraicznej, trygonometrycznej, czy wykładniczej)
![]()
Z okazji roku 2000 ogłoszono
konkurs na najpiękniejszy wzór matematyki. Wygrał wzór
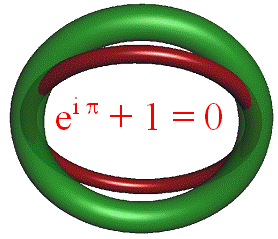
Chyba już wiesz, jak ten wzór powstał ?
|
Zagadka. Po
przeczytaniu powyższych informacji na temat liczb zespolonych nietrudno
będzie odpowiedzieć na pytanie, jaki jest wynik przedstawionego potęgowania
Zdziwisz się, ale
wynikiem jest liczba rzeczywista! |
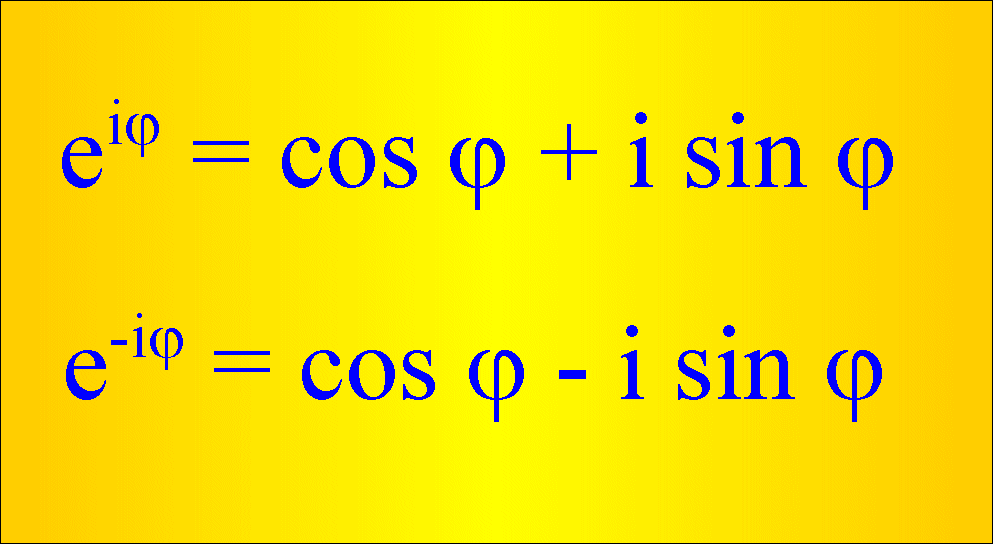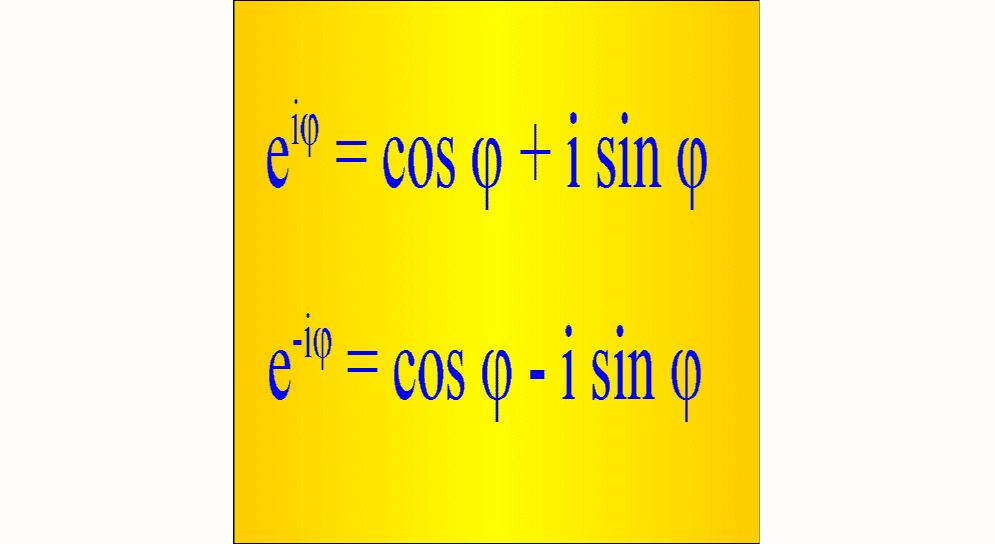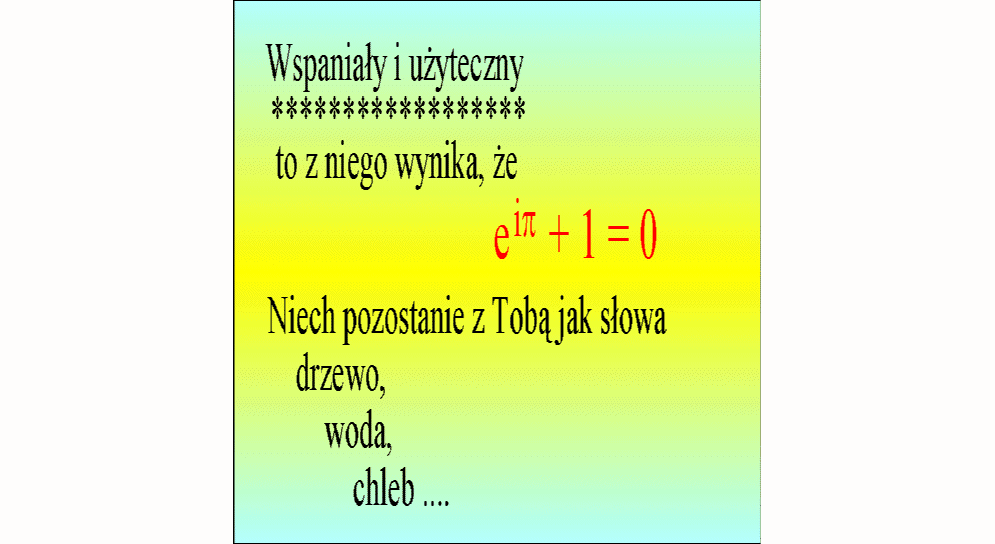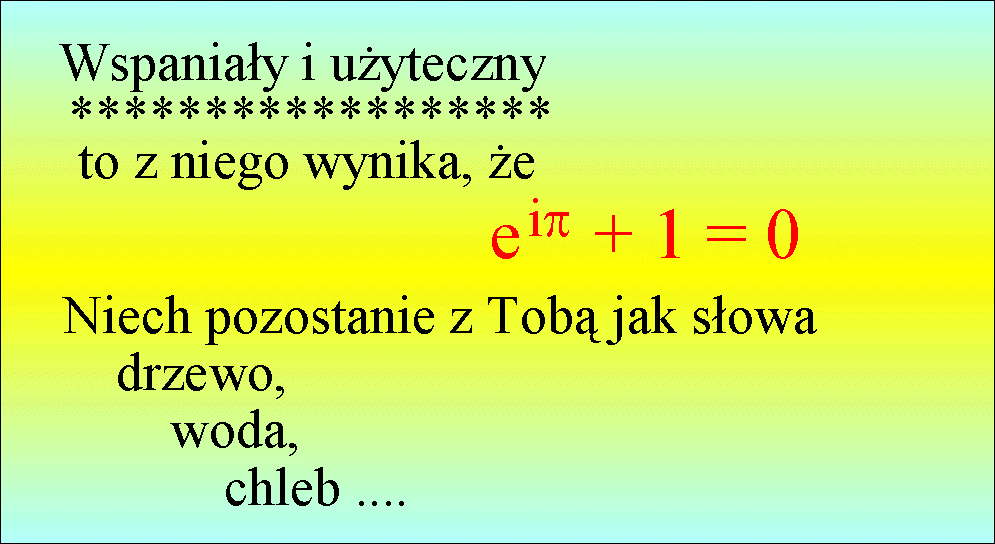
Tajemniczo wyglądający wzór Eulera
można łatwo wyprowadzić. Rozwijając w szereg Maclaurina
![]()
funkcje sin x i cos x otrzymujemy:
![]()
![]()
Jeżeli teraz rozwiniemy w szereg Maclaurina funkcję
exp(ix), to otrzymamy
![]()
co jest sumą rozwinięcia funkcji cos x oraz pomnożonemu
przez i rozwinięcia funkcji sin x :
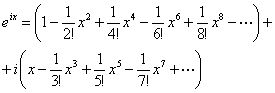
W ten sposób otrzymujemy wzór Eulera:
![]()
Analogicznie otrzymamy:
![]()
Łatwo otrzymać odwrotne związki:
![]()
![]()
|
Zastosowanie wzoru Eulera do
otrzymywania wzorów na funkcje trygonometryczne sum i różnic kątów |
Prostym, ale interesującym zastosowaniem wzoru Eulera jest otrzymywanie wzorów na funkcje trygonometryczne sum i różnic kątów. Gdy chcemy otrzymać np. wzór zastępujący cos(a+b), to stosujemy wzór, który otrzymamy łatwo ze wzoru Eulera
![]()
i zapisujemy go dla przypadku, gdy x = a + b, czyli
![]()
Przekształcamy prawą stronę i stosujemy wzór Eulera do poszczególnych składników

Ostatecznie otrzymujemy poszukiwany wzór
![]()
Wzór ten będziemy wykorzystywali w opisie składania drgań harmonicznych.
Można to też zrobić następująco: Gdy chcemy otrzymać np. sin(a+b), wtedy wypisujemy wzór Eulera, w którym wystąpi sin(a+b):
![]()
Lewą stronę przekształcamy jako
![]()
i dalej
![]()
Grupujemy razem części rzeczywiste i urojone i porównujemy ze wzorem wyjściowym
![]()
Porównujemy części rzeczywiste i części urojone z obu stron równania i otrzymujemy szukane wzory:
![]()
![]()

RÓWNANIA
RÓŻNICZKOWE ZWYCZAJNE O STAŁYCH WSPÓŁCZYNNIKACH
Ogólnie, równanie różniczkowe wiąże ze sobą zmienną niezależną t,
poszukiwaną funkcję x oraz jej pochodne x’, x’’,
x’’’ ...
![]()
Tutaj zajmiemy się tylko takimi równaniami, które będą nam potrzebne do analizy drgań harmonicznych w mechanice i w elektrodynamice. Równania różniczkowe cząstkowe, występujące w opisie ruchu falowego, zostaną przedstawione fragmentarycznie w wykładzie na temat tego ruchu.
Rzędem równania różniczkowego jest rząd najwyższej
pochodnej, jaka występuje w równaniu.
![]()
Jeżeli w równaniu pierwszego rzędu
![]()
funkcja f(t, x) może zostać przedstawiona jako iloczyn
funkcji g(t) i h(x) będących funkcjami tylko t i tylko x, odpowiednio, to
mówimy, że jest to równanie o zmiennych separowalnych. Zatem zmienne x i t w
równaniu
![]()
mogą zostać rozdzielone:
![]()
Pozostaje tylko oddzielnie scałkować obie strony tego
równania:
![]()
![]()
Równanie
typu
![]()
gdzie a i b są stałymi zaś f(t) jest znaną funkcją t jest
nazywane liniowym równaniem różniczkowym drugiego rzędu o stałych
współczynnikach.
Jeżeli
f(t) nie
zależy od t (jest pewna stałą), wtedy równanie
jest nazywane jednorodnym równaniem
różniczkowym, w przeciwnym razie równanie jest niejednorodne.
![]()
Są to
równania o postaci
![]()
Dowolna funkcja x(t) spełniająca równanie jest nazywana
rozwiązaniem szczególnym tego równania. Równanie drugiego rzędu ma dwa takie
rozwiązania szczególne x1(t) i x2(t). Kombinacja liniowa
rozwiązań szczególnych jest rozwiązaniem ogólnym x równania różniczkowego
![]()
gdzie C1 i C2 są dowolnymi stałymi.
W ogólnym przypadku równania jednorodnego rozwiązanie otrzymujemy przez zastosowanie podstawienia
![]()
Przy tym podstawieniu
otrzymujemy
![]()
Po podstawieniu do pierwotnego równania różniczkowego i po
uproszczeniu otrzymujemy równanie
![]()
zwane równaniem charakterystycznym. Jeżeli pierwiastki
równania charakterystycznego λ1 i λ2 są różne, wtedy funkcje
![]()
są rozwiązaniami szczególnymi równania d2x/dt2
+ a dx/dt +bx = 0. Rozwiązaniem ogólnym jest dowolna kombinacja liniowa
rozwiązań szczególnych

Kiedy pierwiastki
równania charakterystycznego są równe, λ1
= λ2 = λ , wtedy
![]()
i rozwiązanie ogólne ma postać
![]()
![]()
Kiedy prawa strona równania
![]()
jest funkcją zmiennej niezależnej t, to równanie jest
niejednorodne.
Rozwiązanie
ogólne równania niejednorodnego jest sumą rozwiązania ogólnego równania
jednorodnego i dowolnego rozwiązania szczególnego równania niejednorodnego

Ponieważ nie ma ogólnej metody znajdowania rozwiązania szczególnego równania niejednorodnego, to tylko od naszych umiejętności i szczęścia będzie zależało, czy będziemy w stanie go znaleźć.
Bardzo
często proste sytuacje fizyczne prowadzą do zagadnień, które są opisywane
przez nieliniowe równania różniczkowe. Równania takie zwykle nie mają rozwiązań
analitycznych i
konieczne jest wtedy stosowanie metod numerycznych. Przykładem może być
proste zadanie wzięte z książki F. Y. Wang – Physics with Maple, Wiley. Wózek o masie m1 jest
uwolniony ze stanu spoczynku w punkcie x = 0 i w czasie t = 0 i jest
ciągnięty po stole przez inną masę m2 spuszczaną pionowo, jak
pokazano na rysunku
Przyjmując, że na powierzchni stołu i na bloku nie występuje tarcie, znaleźć położenie masy m1 jako funkcję czasu. Rozwiązanie. Kąt θ określamy z geometrii układu
Ponieważ kąt θ zmienia się w czasie, to równie w czasie zmienia się siła działająca na m1. Niech naprężenie nici wynosi T, wtedy równanie ruchu dla m1 jest określone przez drugie prawo Newtona
a dla masy m2
Długość nici l jest stała (jest to narzucone ograniczenie ruchu)
Stąd wyznaczymy drugą pochodną
Eliminując T z równań (2) i (3), otrzymujemy
Podstawiając za cos θ i za
dla którego warunkami początkowymi są
Ponieważ to równanie różniczkowe opisujące prostą sytuację nie ma rozwiązania analitycznego, to musimy się posłużyć dla jego rozwiązania metodami numerycznymi. |