MOMENT PĘDU
Prawo
zachowania momentu pędu. Żyroskop.
* Drugie prawo dynamiki dla ruchu obrotowego
* Prawo zachowania momentu pędu
* Podsumowanie II. prawa dynamiki dla ruchu liniowego i .
prawa dynamiki dla ruchu obrotowego
* Zastosowanie prawa zachowania momentu pędu – moment
sił zewnętrznych JEST równy zeru
* Zastosowanie prawa zachowania momentu pędu – moment
sił zewnętrznych NIE JEST równy zeru

W ruchu obrotowym decydującą rolę odgrywają tzw. momenty pewnych
wielkości fizycznych. Dotychczas już zdefiniowaliśmy moment bezwładności
I, który jest zawsze funkcją kwadratu odległości elementów masy od osi obrotu i
dla układu punktów materialnych jest określony wzorem
![]()
a dla brył materialnych jest określony przez całkę
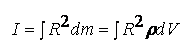
oraz moment siły M, określający relację między wartością siły
zewnętrznej a sposobem jej przyłożenia (punktem przyłożenia i kierunkiem, jaki
tworzy wektor siły F z wektorem ramienia R)
![]()
o wartości
![]()
Trzecim momentem, jaki teraz wprowadzamy, jest krańcowo ważny dla
zrozumienia i opisu zjawisk w ruchu obrotowym moment
pędu L. Moment pędu definiujemy, bardzo podobnie do momentu siły,
jako iloczyn wektorowy promienia wodzącego R elementu masy i wektora
pędu p = mv tego elementu masy.
W ruchu masy m po okręgu o promieniu R z prędkością kątową ω, której odpowiada prędkość liniowa v
moment pędu L będzie produktem iloczynu wektorowego wektorów R i p
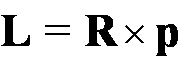
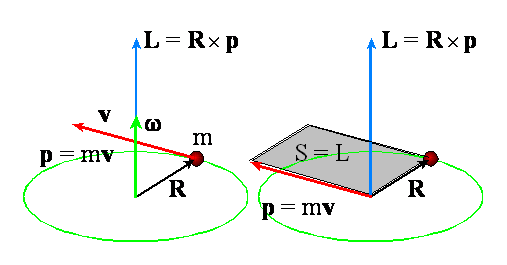
Zobaczmy, jaką korzyść daje nam
nowo zdefiniowany moment pędu. Pamiętając, że p = mv oraz w ruchu po okręgu v =
Rω, możemy napisać w postaci skalarnej, że
![]()
Otrzymaliśmy wspaniały rezultat, który pokazuje, że moment pędu L
wygląda analogicznie jak pęd p, z tym, że zamiast masy m występuje
moment bezwładności I a prędkość liniowa v jest zastąpiona przez
prędkość kątową ω:
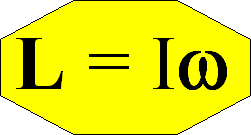
Ten nasz wynik jest słuszny nie tylko dla punktu z masą m obracającego
się po okręgu, ale dla dowolnej bryły mającej moment bezwładności I obracającej
się z prędkością kątową ω.
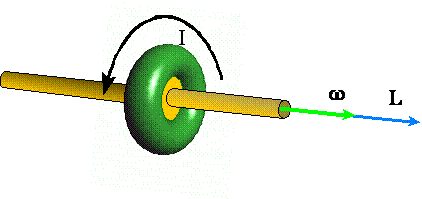
Przypomnijmy otrzymaną analogię
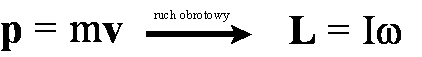
Teraz
otrzymamy naprawdę rewelacyjny wynik! Przez
zróżniczkowanie po czasie obu stron każdego z tych równań otrzymujemy to, co
najważniejsze w mechanice:
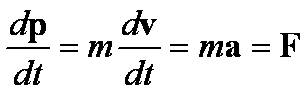
oraz
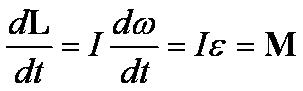
Pierwsze z otrzymanych wyżej
równań jest znaną nam drugą zasadą dynamiki Newtona.


Drugie z otrzymanej pary równań jest odpowiednikiem drugiej zasady dynamiki Newtona obowiązującym w ruchu obrotowym! Mamy w rezultacie bardzo ważny związek między momentem siły zewnętrznej i prędkością zmian momentu pędu
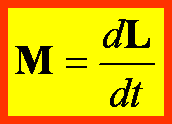
Jest to drugie prawo dynamiki dla ruchu obrotowego, tak samo ważne dla ruchu obrotowego jak dla ruchu postępowego jest ważne uogólnione drugie prawo dynamiki Newtona.
Ponieważ moment siły M jest wielkością addytywną to jeżeli na obracającą się bryłę sztywną działa kilka momentów sił wtedy po lewej stronie powyższego równania umieszczamy sumę wektorową tych momentów:
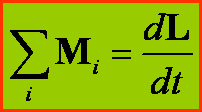


Równanie ![]() prowadzi natychmiast
do prawa zachowania momentu pędu L,
które orzeka, że kiedy moment sił zewnętrznych M jest równy zeru to
moment pędu L obracającej się bryły pozostaje stały jako wielkość
wektorowa. Oznacza to, że bez udziału momentu sił zewnętrznych M moment
pędu L nie może zmienić nie tylko swojej długości ale także i kierunku. Rzeczywiście,
jeżeli w równaniu
prowadzi natychmiast
do prawa zachowania momentu pędu L,
które orzeka, że kiedy moment sił zewnętrznych M jest równy zeru to
moment pędu L obracającej się bryły pozostaje stały jako wielkość
wektorowa. Oznacza to, że bez udziału momentu sił zewnętrznych M moment
pędu L nie może zmienić nie tylko swojej długości ale także i kierunku. Rzeczywiście,
jeżeli w równaniu ![]() podstawimy
podstawimy ![]() to wtedy
to wtedy
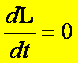
co oznacza, że gdy nie występują zewnętrzne momenty sił, to
![]()


Skutek, jaki zostanie wywołany przez przyłożenie momentu siły zależy nie tylko od wartości tego momentu, ale i od czasu, w którym ten moment działa. Skutek ten opisujemy jedną wielkością zwaną impulsem (popędem) kątowym J, analogicznie jak to robiliśmy dla przypadku impulsu siły. Ponieważ
![]()
to
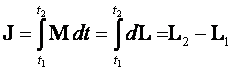
Otrzymaliśmy wyrażenie, które mówi, że zadziałanie impulsem J powoduje przyrost momentu pędu ciała L2 – L1.

PODSUMOWANIE
DRUGIEGO PRAWA DYNAMIKI DLA RUCHU
LINIOWEGO
I
DRUGIEGO PRAWA DYNAMIKI DLA RUCHU
OBROTOWEGO
UOGÓLNIONA DRUGA ZASADA DYNAMIKI NEWTONA
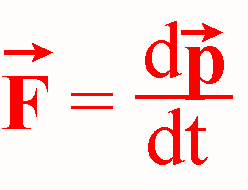
WRAZ Z
UNIWERSALNĄ DLA CAŁEJ PRZYRODY
ZASADĄ ZACHOWANIA ENERGII
JEST ZAANGAŻOWANA
WE WSZYSTKICH ZJAWISKACH I PROCESACH,
W KTÓRYCH DZIAŁAJĄ
JAKIEKOLWIEK SIŁY
Kiedy uwzględnimy relatywistyczną zmianę masy m
poruszającego się ciała o masie spoczynkowej m0 i prędkości v i
kiedy uwzględnimy fakt, że prędkość światła w próżni c jest wielkością stałą
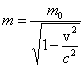
wtedy z równania ![]() otrzymujemy
najsławniejszy wzór fizyki
otrzymujemy
najsławniejszy wzór fizyki
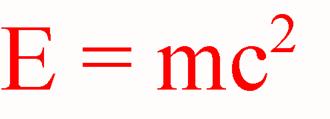
wyrażający równoważność masy i energii.
UOGÓLNIONA DRUGA ZASADA DYNAMIKI NEWTONA DLA RUCHU
POSTĘPOWEGO MA SWÓJ ODPOWIEDNIK TAKŻE DLA RUCHU OBROTOWEGO.
W PRZYPADKU RUCHU POSTĘPOWEGO OPISUJE ONA ZWIĄZEK MIĘDZY DZIAŁAJĄCĄ SIŁĄ F, A PRĘDKOŚCIĄ ZMIANY PĘDU dp/dt
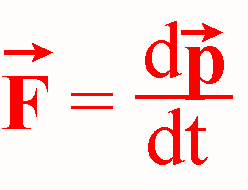
ZACHODZĄCEJ POD DZIAŁANIEM TEJ SIŁY.
W PRZYPADKU RUCHU OBROTOWEGO UOGÓLNIONA DRUGA ZASADA DYNAMIKI OPISUJE ZWIĄZEK MIĘDZY DZIAŁAJĄCYM MOMENTEM SIŁY M, A PRĘDKOŚCIĄ ZMIANY MOMENTU PĘDU dL/dt ZACHODZĄCEJ POD DZIAŁANIEM TEGO MOMENTU SIŁY
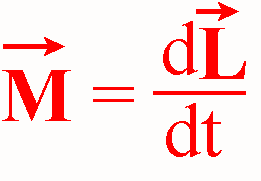
W praktyce bardzo użyteczne są uproszczone wersje tych równań.
Kiedy masa poruszającego się ciała m nie zmienia się w
czasie trwania ruchu, wtedy równanie
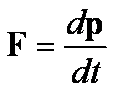 przechodzi w
równanie
przechodzi w
równanie ![]()
Kiedy moment bezwładności I obracającej się bryły
sztywnej nie zmienia się w czasie trwania ruchu, wtedy równanie
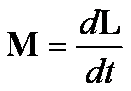 przechodzi w równanie
przechodzi w równanie ![]()


Przykład 1. Rozważmy następującą sytuację: dwie tarcze o momentach bezwładności I1 i I 2 kręcą się współosiowo niezależnie od siebie z prędkościami kątowymi ω1 i ω2
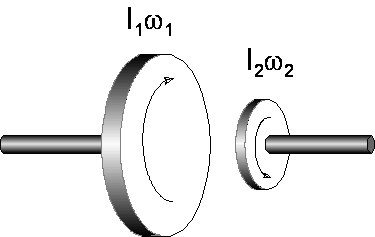
Działając siłami F skierowanymi wzdłuż osi obrotu ściskamy tarcze tak, że te zaczynają się teraz obracać ze wspólną prędkością kątową ω
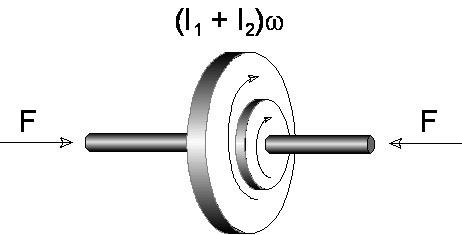
Dlaczego w tym przypadku możemy stosować prawo zachowania momentu pędu?
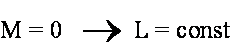
Jaka będzie wspólna dla obu tarcz prędkość kątowa ω? Stosując zasadę zachowania momentu pędu, możemy napisać
![]()
Stąd
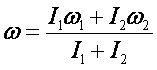
Sprawdzić, czy w procesie łączenia dysków zostanie spełniona zasada zachowania energii kinetycznej ruchu obrotowego. W czasie zetknięcia tarcz na ogół wystąpi zgrzyt i może buchnąć płomień. Jaka energia wydzieli się w postaci dźwięku i ciepła?
Przykład 2. Obracający się na krześle obrotowym człowiek trzyma w rękach hantle. Przyciągając i oddalając hantle od swego korpusu może on zmieniać swoją prędkość kątową zgodnie z zasadą L = const. Jak zmienia się jego prędkość kątowa, gdy człowiek na przemian odsuwa hantle od swego korpusu i przyciąga je z powrotem?
Przyjmujemy, że człowiek siedzący na krześle obrotowym jest izolowany od działania zewnętrznych momentów sił, czyli że jego moment pędu L jest stały. Oznacza to, że stały jest także iloczyn jego momentu bezwładności I i prędkości kątowej ω w obu przypadkach, kiedy odsunął hantle daleko od siebie i kiedy je przyciągnął:
![]()
W rezultacie, dla dużego momentu bezwładności (odsunięte hantle) prędkość kątowa będzie mała (wolne wirowanie) a dla małego momentu bezwładności (przyciągnięte hantle) prędkość kątowa będzie duża (szybkie wirowanie).
Analogicznie zachowuje się prędkość kątowa (wirowanie w piruecie) tancerki, która nadaje sobie prędkość obrotową mając rozłożone ręce i odchyloną w bok jedną nogę. Kiedy następnie tancerka kręcąc się na czubku swojego bucika (poincie) lub łyżwy ściąga kończyny ku osi swego ciała, wtedy wchodzi w szybkie wirowanie zwane piruetem.


ŻYROSKOP. Już wiemy, że jeżeli na ciało rotujące z momentem pędu L nie działa żaden moment siły zewnętrznej M, to wektor L nie może ulec zmianie, czyli nie może zmienić ani wartości, ani kierunku, ani zwrotu. Na tej zasadzie działają wszelkiego typu urządzenia żyroskopowe, jak np. kompasy żyroskopowe i stabilizatory żyroskopowe.
Jeżeli
jednak pojawi się moment siły zewnętrznej, gdy np. podeprzemy żyroskop tylko z
jednej strony to niezrównoważona siła ciężkości mg o ramieniu działania R spowoduje
powstanie momentu siły M, który wywoła przyrost momentu pędu dL =
Mdt
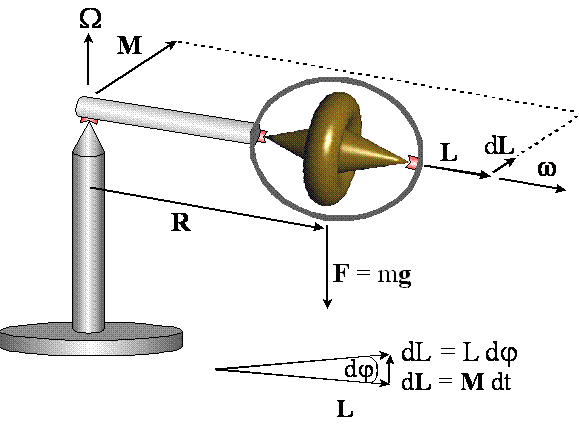
Ponieważ dt jest skalarem, to oba wektory M i dL są równoległe. Przyrost wektora L o dL oznacza skręcenie osi obrotu i obrót żyroskopu w płaszczyźnie poziomej z częstotliwością kątową Ω. Tę częstotliwość kątową Ω obrotu w płaszczyźnie poziomej nazywamy częstotliwością precesji.
Wartość częstotliwości precesji znajdziemy z prostego rozumowania. Jeżeli po czasie dt oś żyroskopu skręci o kąt dφ, to moment pędu L przyrośnie o wartość dL = L dφ.
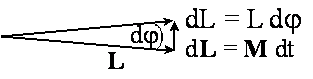
Dzieląc to równanie dL = L dφ obustronnie przez dt i pamiętając, że L = Iω, mamy
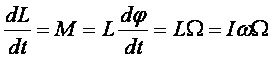
i ostatecznie znajdujemy związek między obiema częstotliwościami kątowymi w postaci
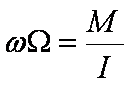
Urządzenia żyroskopowe wykorzystuje się w urządzeniach nawigacyjnych jako busole, żyroskopy kursowe, a w lotnictwie dodatkowo jako zakrętomierze i piony żyroskopowe. Potężne żyroskopy umieszczane w płaszczyźnie symetrii dużych statków służą jako stabilizatory przechyłu (przechył statku, dzięki działaniu tego żyroskopu, jest zamieniany na zmianę kierunku osi statku, a ta zmiana jest łatwo tłumiona przez opór wody). Niedawno pojawiły się modele myszek komputerowych działających przestrzennie, w których sygnał położenia przestrzennego myszki jest generowany w wyniku obracania osi żyroskopu sprzężonego z myszką.
|
Przykład 3. Przedyskutować skręcanie roweru bez użycia kierownicy po nachyleniu się rowerzysty w prawo lub w lewo. |
Dla łatwiejszego przechodzenia między wzorami dla ruchu liniowego i dla ruchu obrotowego wygodnie zapamiętać dosyć oczywiste analogie wielkości fizycznych w obu typach ruchu
|
Ruch postępowy |
t |
s |
v |
a |
m |
p |
F |
|
Ruch obrotowy |
t |
φ |
ω |
ε |
I |
L |
M |