Back to Index

FALE ELEKTROMAGNETYCZNE

-RÓWNANIE FALOWE Z RÓWNAŃ MAXWELLA

STRUKTURA FALI ELEKTROMAGNETYCZNEJ

PRĘDKOŚĆ FAL ELEKTROMAGNETYCZNYCH

* Otrzymywanie równania falowego z równań Maxwella

* Struktura fali elektromagnetycznej

* Prędkość fal elektromagnetycznych

JAK ZAPOWIADALIŚMY TO JUŻ WCZEŚNIEJ, WPROWADZENIE PRZEZ MAXWELLA GENIALNEJ KONCEPCJI PRĄDU PRZESUNIĘCIA I DODANIE TEGO PRĄDU DO ZWYKŁEGO PRĄDU PRZEWODZENIA DOPROWADZIŁO DO STWORZENIA UOGÓLNIONEGO PRAWA AMPERA. BIORĄC ZA PODSTAWĘ DWA RÓWNANIA: RÓWNANIE WYRAŻAJĄCE PRAWO FARADAYA ORAZ RÓWNANIE WYRAŻAJACE UOGÓLNIONE PRAWO AMPERA WYPROWADZIMY RÓWNANIE RÓZNICZKOWE OPISUJĄCE FALE ELEKTROMAGNETYCZNE.

Równanie różniczkowe opisujące ruch falowy w ośrodkach sprężystych zostało przez nas otrzymane w wykładzie 16. Jest to równanie różniczkowe drugiego rzędu o pochodnych cząstkowych i dla fali rozchodzącej się w kierunku osi x z prędkością v ma ono postać

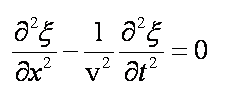
Zmienna ξ , będąca funkcją położenia i czasu, ξ = ξ(x, t), oznacza lokalne, chwilowe wychylenie w ruchu falowym. Może to być wychylenie punktu falującej membrany w fali poprzecznej czy też ciśnienie w danym punkcie i w określonej chwili w fali podłużnej.

Rozwiązaniem równania falowego dla fali poruszającej się w dodatnim kierunku osi x jest

a dla fali poruszającej się w ujemnym kierunku osi x w argumencie funkcji sinus znajdzie się znak plus:

Teraz naszym celem jest znalezienie równania falowego, w którym zmienna ξ stanie się konkretną wartością pola elektrycznego E lub pola magnetycznego B. Podstawą do otrzymania tego równania będą prawo Faradaya (pierwsze równanie Maxwella) oraz uogólnione prawo Ampera (drugie równanie Maxwella), oba w postaci różniczkowej:

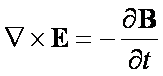
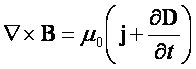
Będziemy poszukiwali równania dla fal elektromagnetycznych rozchodzących się w próżni gdzie nie będą występowały prądy przewodzenia. W związku z tym gęstość prądu j będzie równa zeru i nasz układ równań ulegnie uproszczeniu:

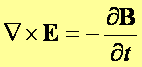
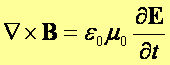
Na podstawie tych właśnie równań będziemy poszukiwali równania fal elektromagnetycznych. Okazuje się, że w fali elektromagnetycznej w próżni wektory E i B drgają w płaszczyznach wzajemnie prostopadłych i dla fali rozchodzącej się w kierunku osi x możemy przyjąć taki układ odniesienia aby wektor E drgał w kierunku osi y a wektor B w kierunku osi z. Zatem wektory E i B mają tylko po jednej składowej

Wykorzystamy metodę znajdowania za pomocą wyznacznika składowych wektora będącego iloczynem wektorowym dwóch innych wektorów {wykład 2) do znalezienia rotacji rot E i rot B dla wektorów E = [0, E, 0] i B = [0, 0, B]:

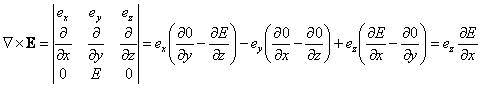
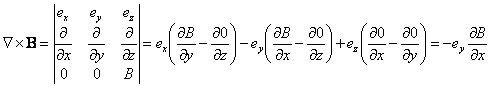
Tutaj wykorzystaliśmy fakt, że nasza fala jest falą płaską i pola E i B zmieniają się tylko względem współrzędnej x, czyli że oraz . Podstawiając otrzymane wartości rotacji do równań Maxwella i pamiętając, że oraz dostajemy układ dwóch równań

W rezultacie do rozwiązania mamy układ dwóch równań:

Równania falowe dla E i B będą miały identyczną postać i otrzymuje się je w taki sam sposób. Jeżeli zdecydujemy się szukać równania dla E, to eliminujemy z naszego układu równań B przez utworzenie pochodnych mieszanych B względem x i t. Różniczkujemy zatem pierwsze równanie po x, a drugie po t:

W wyniku tej operacji otrzymujemy

Po wyeliminowaniu pochodnej mieszanej otrzymujemy poszukiwane równanie falowe dla pola E:

Jest to równanie analogiczne do znanego nam z mechaniki równania falowego

Prędkością fali elektromagnetycznej w próżni jest prędkość światła w próżni c (światło jest także falą elektromagnetyczną) i równanie falowe dla pola E ma ostateczną postać:

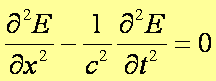
Jednocześnie otrzymujemy związek między wartością c a wartościami przenikalności elektrycznej i magnetycznej próżni 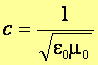. Dokładnie tak samo znajdujemy równanie falowe dla pola B.

Rozwiązania równań falowych dla E i B mają jednakowe postacie

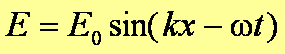
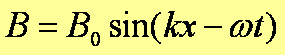
E₀ i B₀ są amplitudami pól elektrycznego i magnetycznego w fali elektromagnetycznej. Długość fali λ = cT, gdzie T jest okresem drgań. Podobnie jak w rozwiązaniu dla fal mechanicznych, tutaj także zastosowano wektor falowy (zwany także stałą propagacji) k = 2π/λ oraz częstotliwość kątową ω wyrażoną przez wektor falowy ω = ck.

Istotą fali sprężystej jest rozchodzenie się deformacji ośrodka sprężystego z powtarzającą się okresowo zamianą energii potencjalnej w kinetyczną.

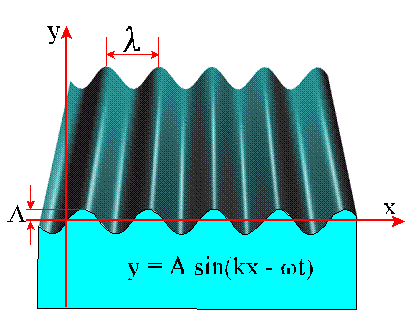
Fala elektromagnetyczna ma zupełnie inną naturę. W fali elektromagnetycznej nie występuje. zamiana dwóch rodzajów energii a ponieważ może się ona rozchodzić także w próżni to ta fala jest raczej „falą istnienia” niż falą deformacji. Modelem fali istnienia może być tłum ludzi opuszczający tunel metra po przyjeździe pociągu. Na początku idzie czołówka najszybszych pasażerów, za nią zasadnicza grupa zamykana przez najbardziej zmęczonych. Po kilku minutach, kiedy nadjedzie następny pociąg, sytuacja się powtarza. Mamy zatem do czynienia z falą istnienia grup ludzi. Z falą o podobnym charakterze będziemy mieli do czynienia kiedy naelektryzowaną kulę schowamy do wnętrza uziemionego pudła metalowego. Pole elektryczne, które otaczało kulę, teraz znika, ale najpierw w najbliższym otoczeniu. W miejscach oddalonych pole jeszcze istnieje i zniknie dopiero wtedy, kiedy dotrze tam obszar stanowiący granicę zanikającego pola. Zmiany w natężeniu pola rozchodzą się w próżni z prędkością światła c. Pole pojawi się ponownie, ale najpierw w najbliższym otoczeniu wtedy, kiedy ponownie wyjmiemy kulę z pudła. Do miejsc oddalonych pole będzie docierało także z prędkością c. Przez okresowe wyjmowanie i chowanie naelektryzowanej kuli wytworzymy falę elektromagnetyczną, chociaż prawie na pewno nie będzie to fala sinusoidalna.

W sinusoidalnej fali elektromagnetycznej opisywanej przez otrzymane wyżej rozwiązania równania falowego pola E i B zmieniają się w płaszczyznach wzajemnie prostopadłych

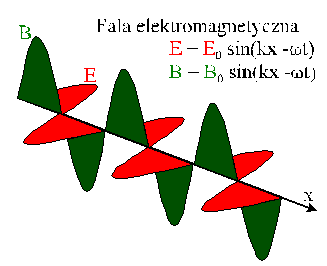
Jak widać, nie występuje tutaj żadna zamiana dwóch rodzajów energii – pole elektryczne E i pole magnetyczne B mają równocześnie wartości maksymalne i równocześnie stają się zerem. Jest możliwe dlatego, że mamy do czynienia z „falą istnienia”. Wektory E i B w fali elektromagnetycznej

● są względem siebie prostopadłe a także są prostopadłe do kierunku rozchodzenia się fali, czyli fale elektromagnetyczne są falami poprzecznymi

● zmieniają się w tej samej fazie, czyli jednocześnie mają wartość maksymalną i jednocześnie stają się zerem.

Szczególną uwagę poświęcimy składowej elektrycznej fali elektromagnetycznej, zwłaszcza w przypadku światła, które także jest falą elektromagnetyczną. Chociaż składowej elektrycznej fali zawsze towarzyszy jej składowa magnetyczna, to właśnie pole E światła oddziałuje z naszym wzrokiem, z matrycami CMOS lub CCD aparatów fotograficznych i kamer, to właśnie ono jest odpowiedzialne za fotosyntezę w roślinach itd.

W ogólnym przypadku wektor E może przyjmować dowolne kierunki w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali. Można jednak tak uformować falę, aby wektor E miał stały kierunek lub zmieniał się w sposób regularny. Tak uformowaną falę poprzeczną nazywamy falą spolaryzowaną. Kiedy wektor E drga stale w jednej płaszczyźnie, to taką falę nazywamy liniowo spolaryzowaną.

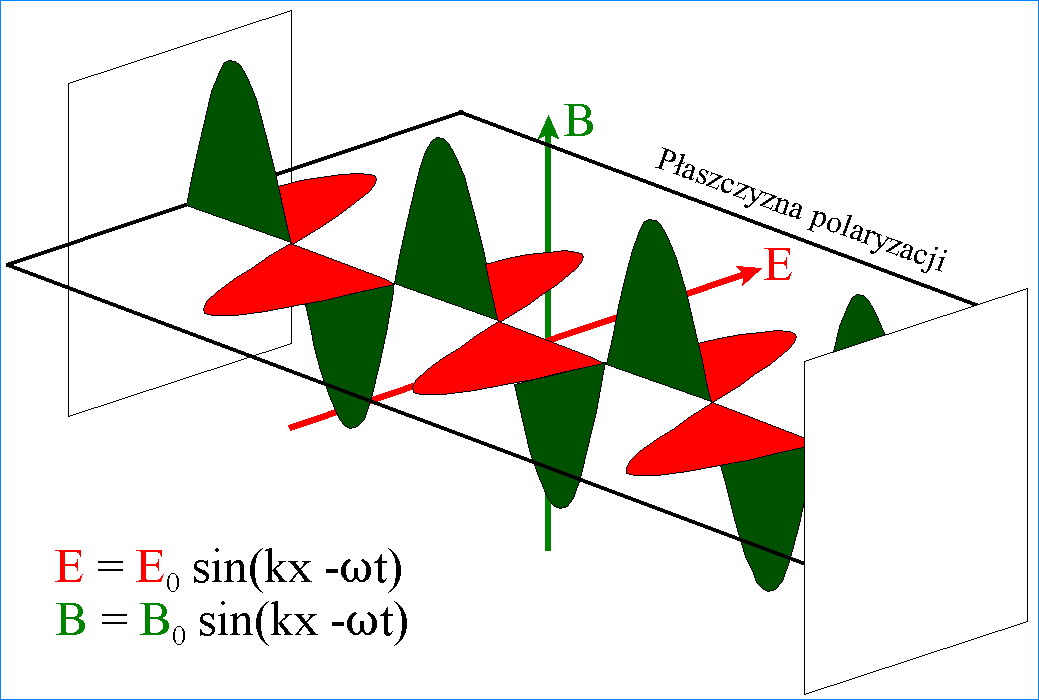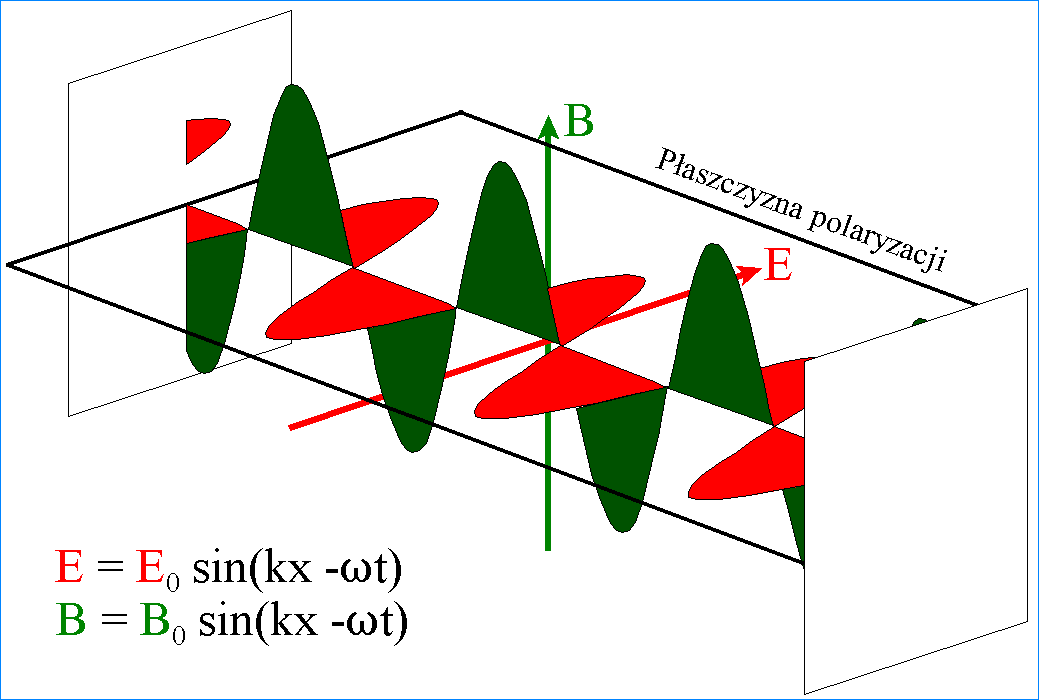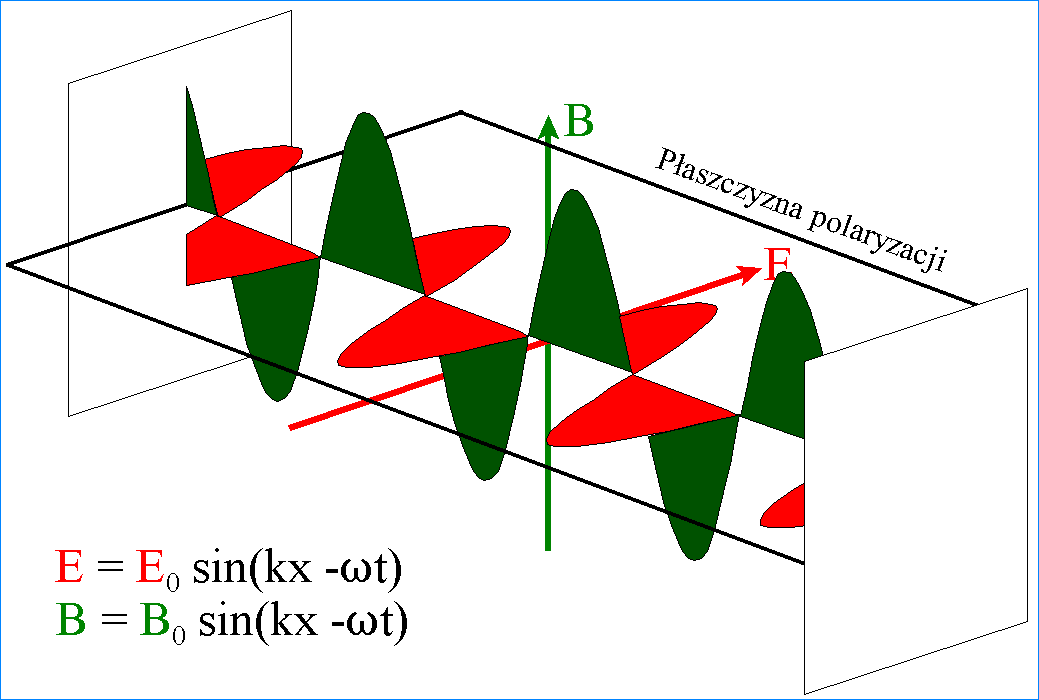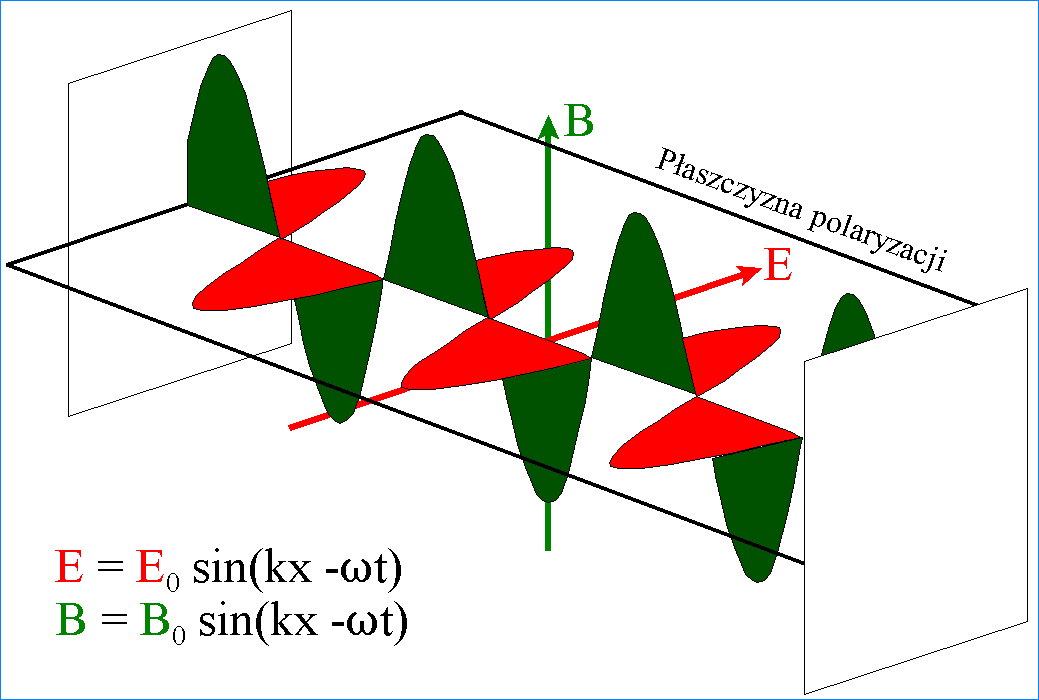
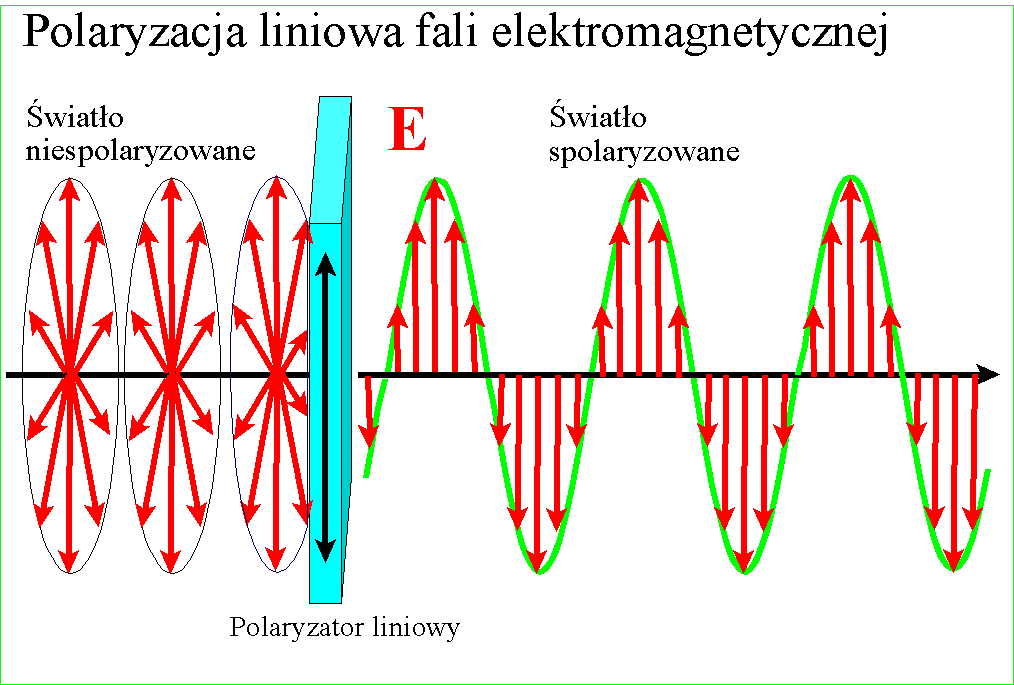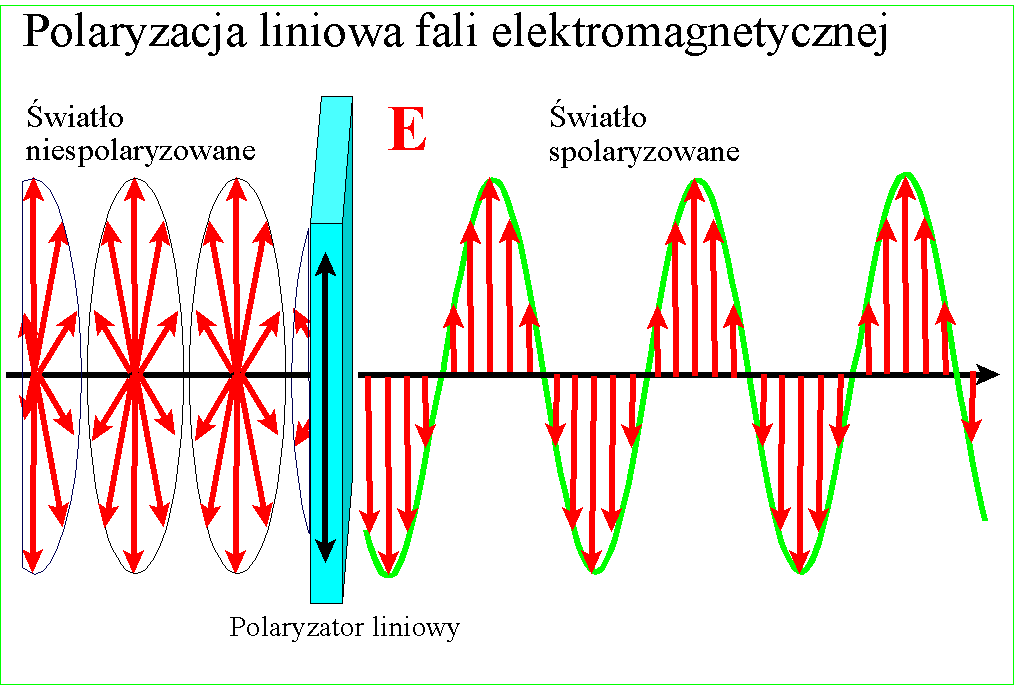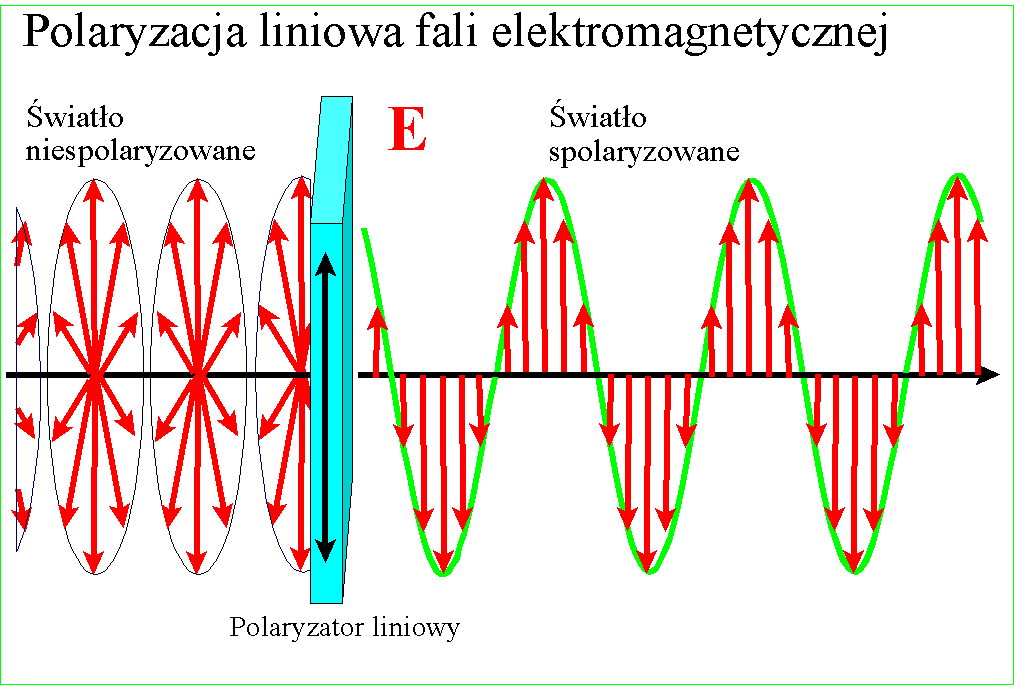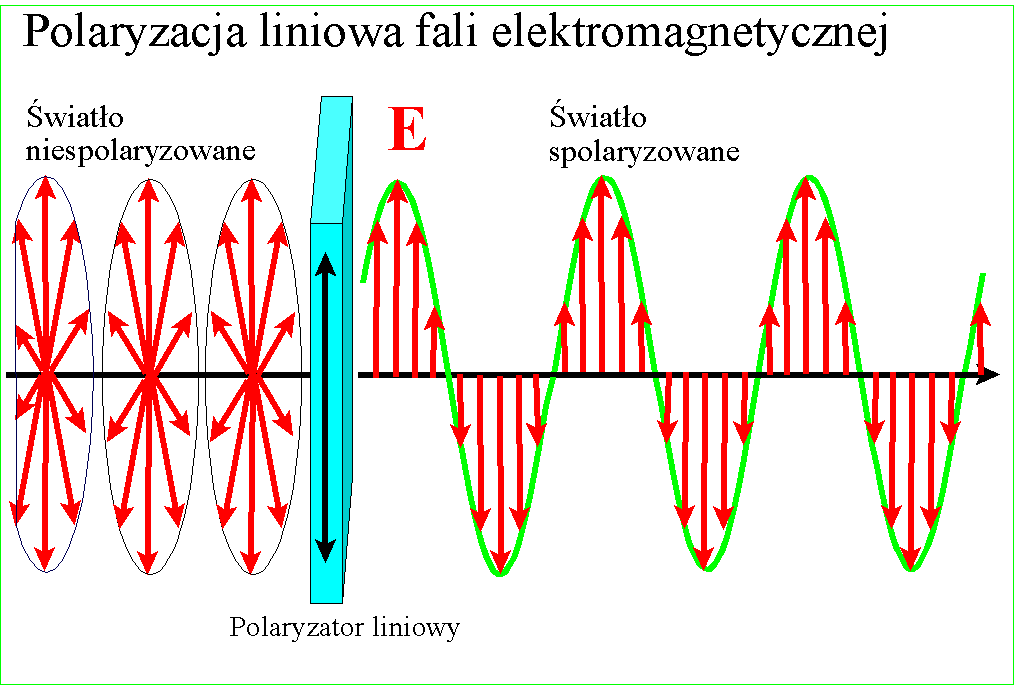
W przypadku, kiedy mamy do czynienia z wiązką fal (wiązką światła), polaryzacja polega na usunięciu z fali drgań niepożądanych, zwykle przez pochłanianie, odbicie lub załamanie. Element optyczny służący do otrzymywania wiązki spolaryzowanej liniowo nosi nazwę polaryzatora lub filtru polaryzacyjnego. Jego działanie obrazuje animacja:

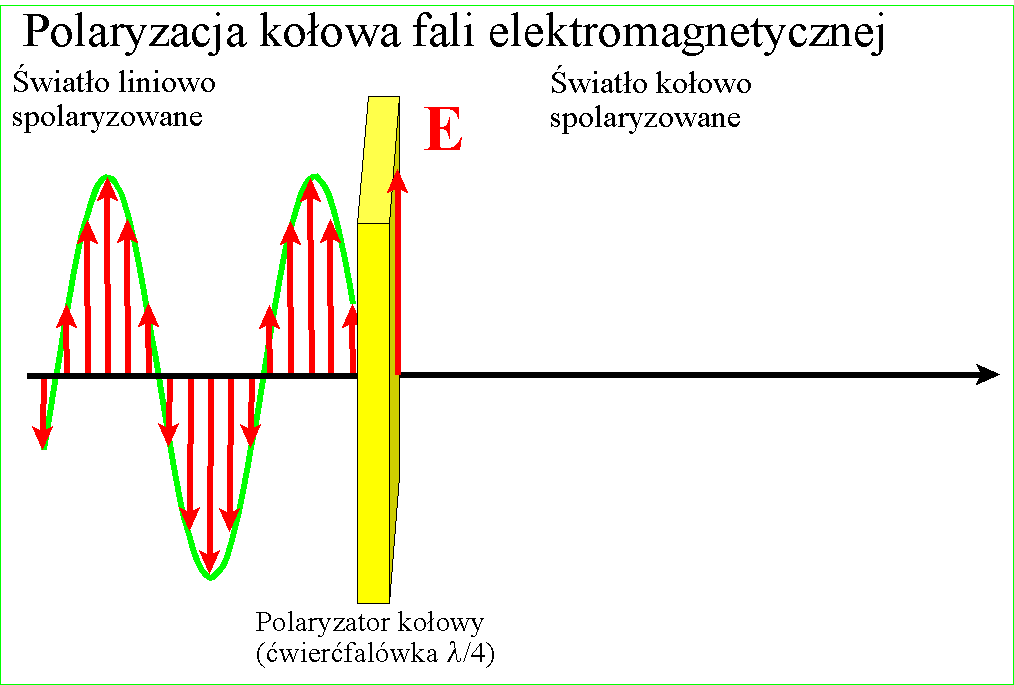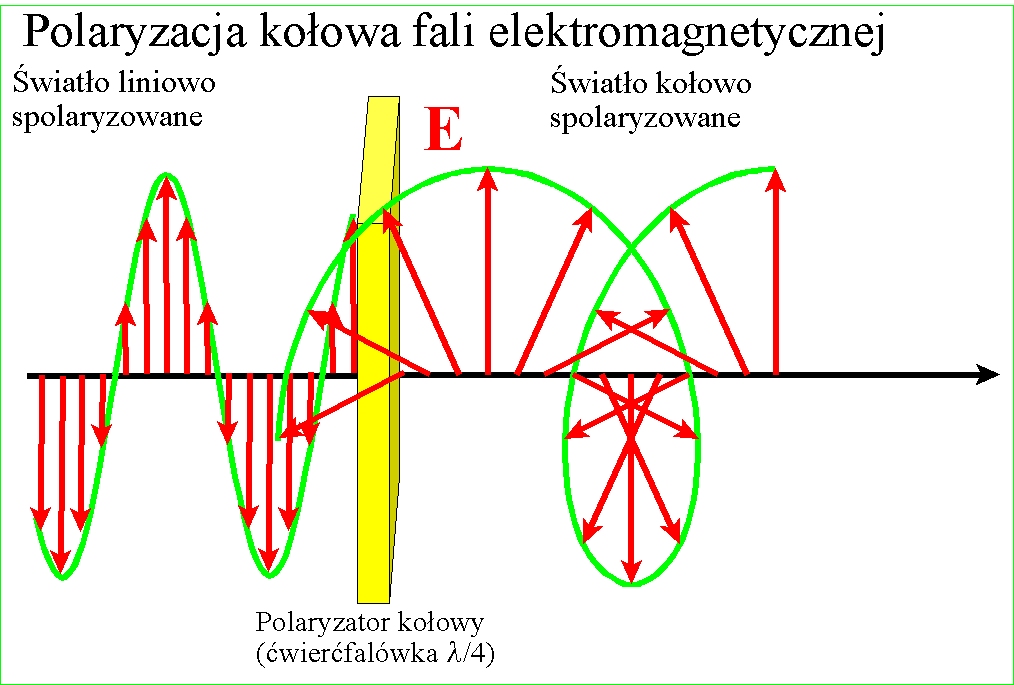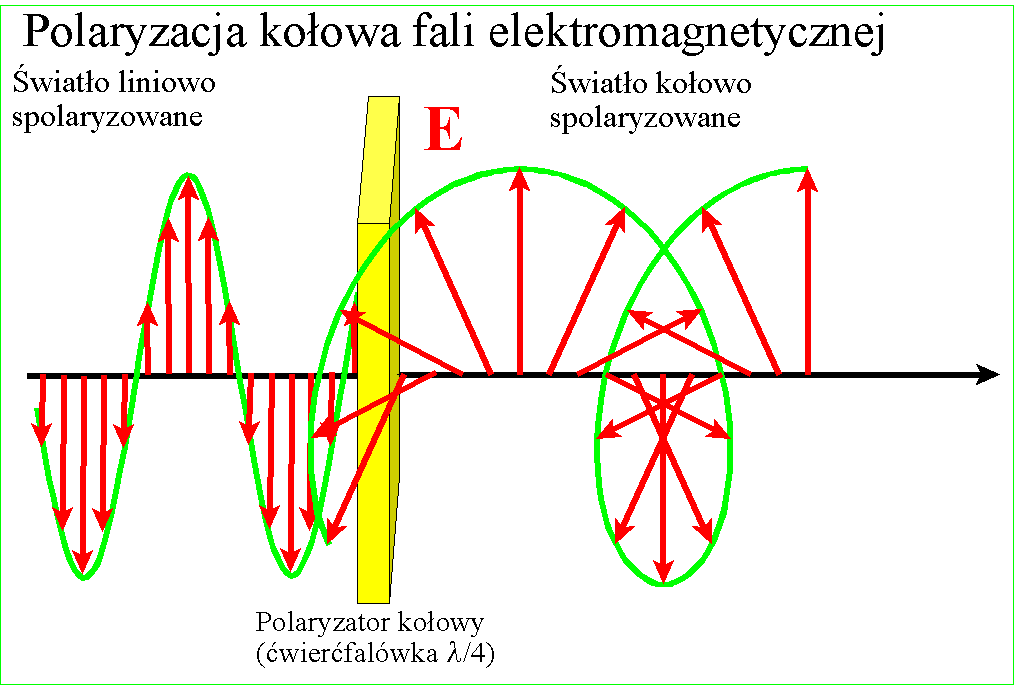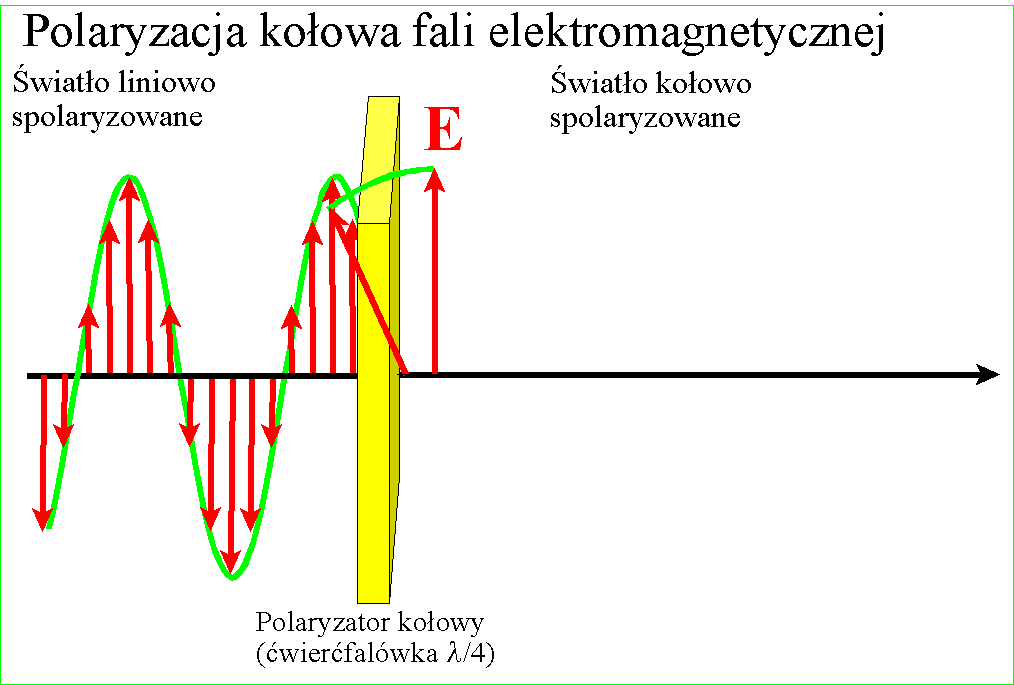
Kiedy koniec wektora E zakreśla w przestrzeni okrąg lub elipsę, to taką falę nazywamy spolaryzowaną kołowo lub eliptycznie Fala spolaryzowana kołowo lub eliptycznie powstaje z fali spolaryzowanej liniowo przez przepuszczenie jej przez płytkę, która powoduje przesunięcie fazy między rzutami wektora E na dwa prostopadłe kierunki. Jeżeli oba te rzuty wektora E mają takie same długości, a przesunięcie fazy między nimi wynosi 90^o (zastosowaliśmy odpowiednio ustawioną płytkę zwaną ćwierćfalówką) to otrzymuje się falę kołowo spolaryzowaną.

Przepuszczenie światła kołowo spolaryzowanego przez ćwierćfalówkę daje ponownie falę liniowo spolaryzowaną.

Jak to pokazaliśmy wyżej, prędkość światła w próżni wynosi

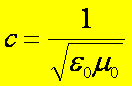
W układzie SI prędkość światła w próżni jest ustalona przez przyjęcie uzgodnienia co do jej wartości i obecnie ta prędkość nie podlega już pomiarom. Przyjęto, że

c = 2.997 924 58 × 10⁸ m s^-1

W praktyce zwykle wystarcza przybliżenie c = 300 000 km s^-1. W ośrodku materialnym o przenikalnościach względnych ε_r i μ_r prędkość fali elektromagnetycznej v wynosi

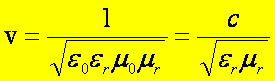
Współczynnik załamania n ośrodka jest definiowany jako stosunek prędkości fali w próżni c do prędkości fali w tym ośrodku v (uwzględniamy fakt, że μ_r ośrodka, w którym światło może się rozchodzić jest bliski 1)

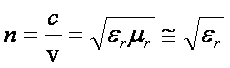
czyli

Back to Index