Back to Index

RÓWNANIA MAXWELLA

POSTACI RÓŻNICZKOWA I CAŁKOWA

* Otrzymywanie postaci różniczkowej prawa Faradaya

* Otrzymywanie postaci różniczkowej uogólnionego prawa Ampera

* Otrzymywanie postaci różniczkowej prawa Gaussa dla pola elektrycznego

* Otrzymywanie postaci różniczkowej prawa Gaussa dla pola magnetycznego

* Równania Maxwella - podsumowanie

STOSUJĄC TWIERDZENIE GAUSSA-OSTROGRADSKIEGO I TWIERDZENIE STOKESA ZAMIENIMY RÓWNANIA MAXWELLA Z POSTACI CAŁKOWEJ DO POSTACI RÓŻNICZKOWEJ

Prawo Faradaya – postać całkowa: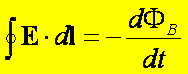

Na podstawie twierdzenia Stokesa zamieniamy całkę liniową (cyrkulację) z lewej strony równania na całkę powierzchniową

Prawą stronę w prawie Faradaya możemy zapisać w postaci

Teraz możemy przyrównać obie całki powierzchniowe

Stosujemy tutaj pochodną cząstkową ∂B/∂t ponieważ pole B może zależeć także od położenia. Z równości całek powierzchniowych dla dowolnych powierzchni wynika równość funkcji podcałkowych.

Otrzymujemy więc prawo Faradaya – postać różniczkowa: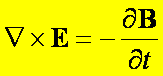

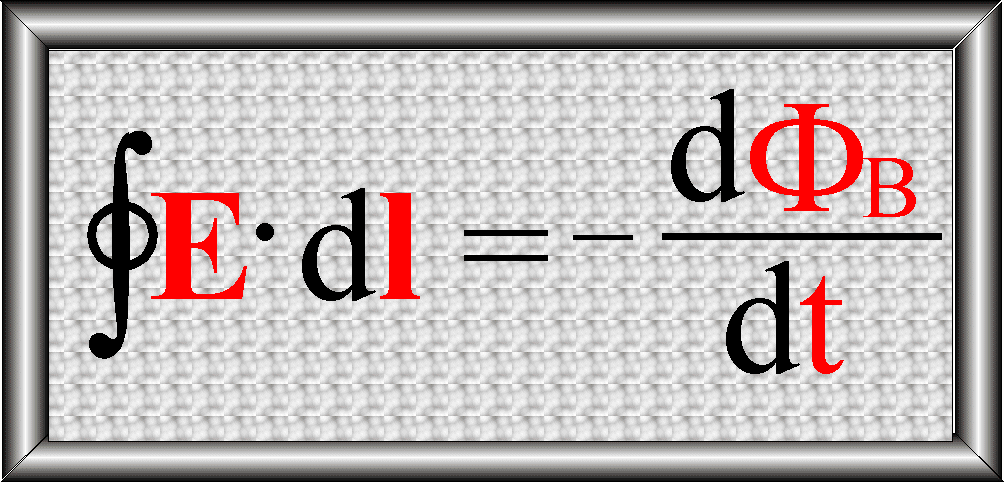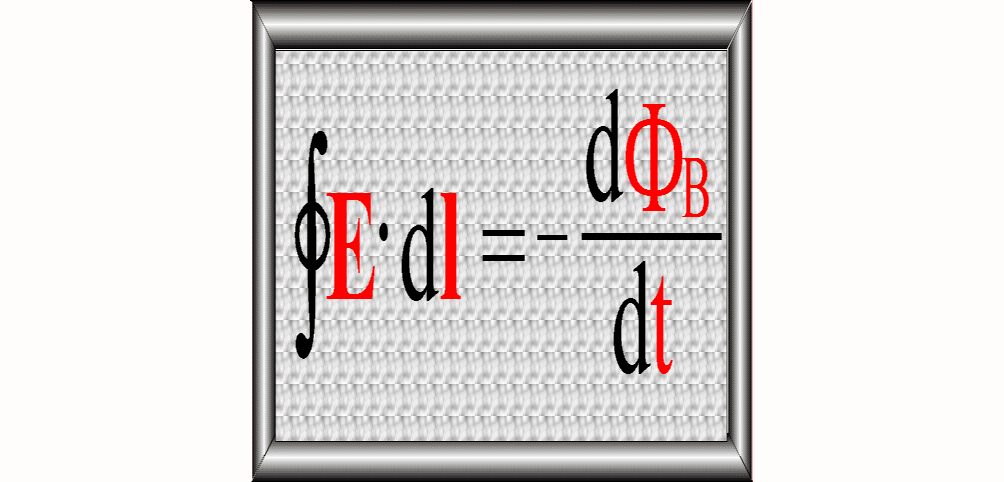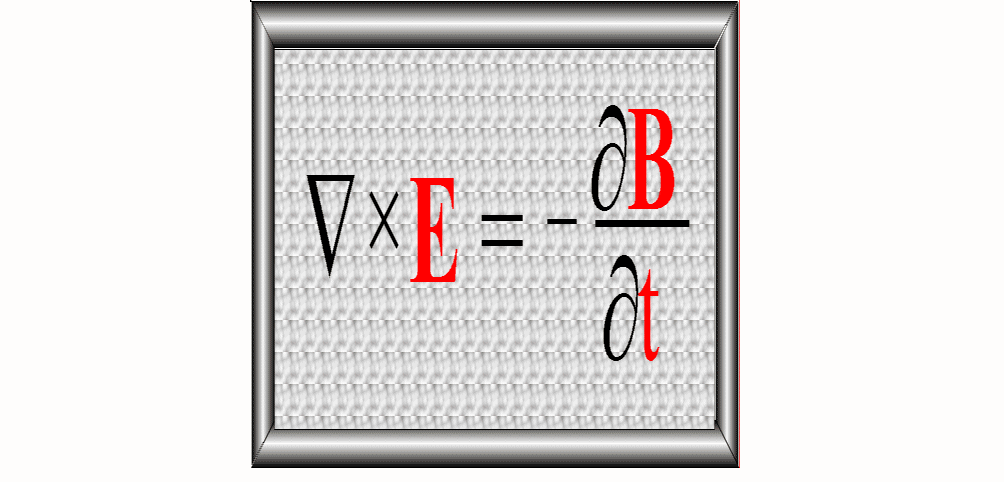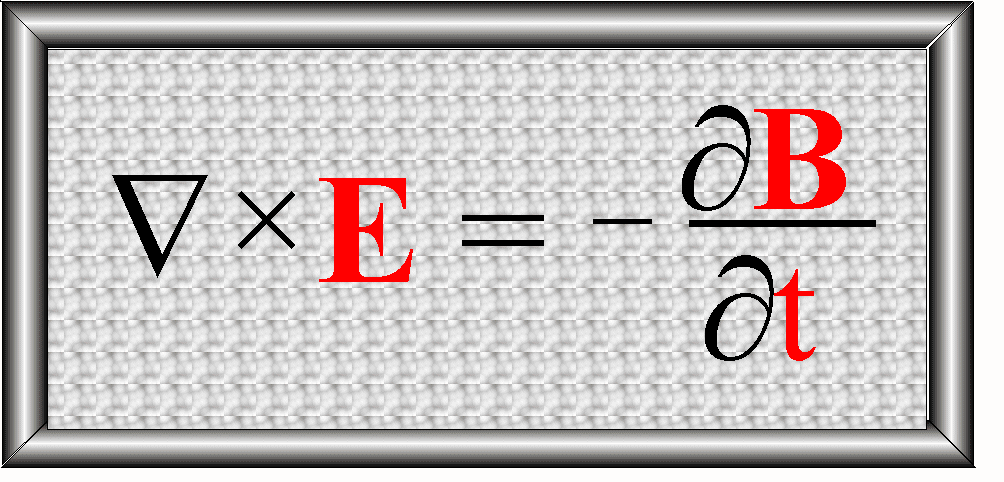
Uogólnione prawo Ampera – postać całkowa: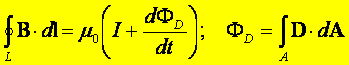

Na podstawie twierdzenia Stokesa zamieniamy całkę liniową (cyrkulację) z lewej strony równania na całkę powierzchniową

Prawą stronę w uogólnionym prawie Ampera możemy przedstawić jako całkę powierzchniową

Po uwzględnieniu, że prąd przewodzenia I może być wyrażony przez gęstość prądu j

prawą stronę zapiszemy jako jedną całkę powierzchniową

Przyrównujemy teraz do siebie obie całki powierzchniowe

Aby to równanie było prawdziwe dla każdej powierzchni A, niezależnie od jej rozmiarów i kształtu, funkcje podcałkowe po obu stronach równania muszą być równe.

Otrzymujemy więc uogólnione prawo Ampera – postać różniczkowa::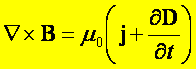

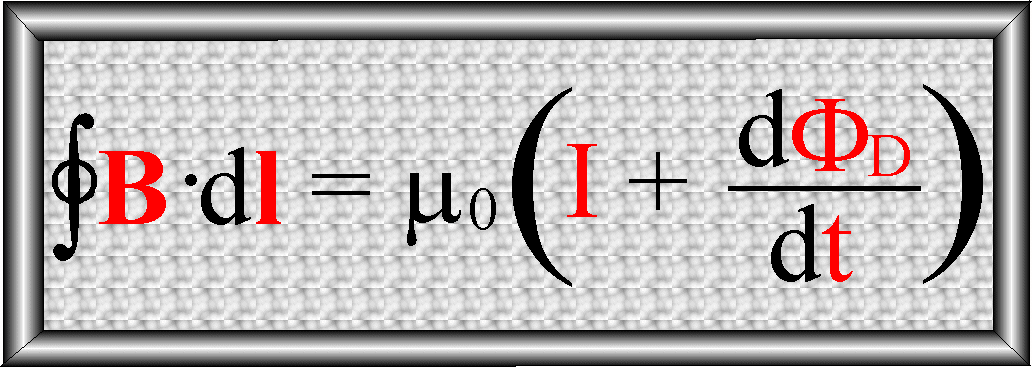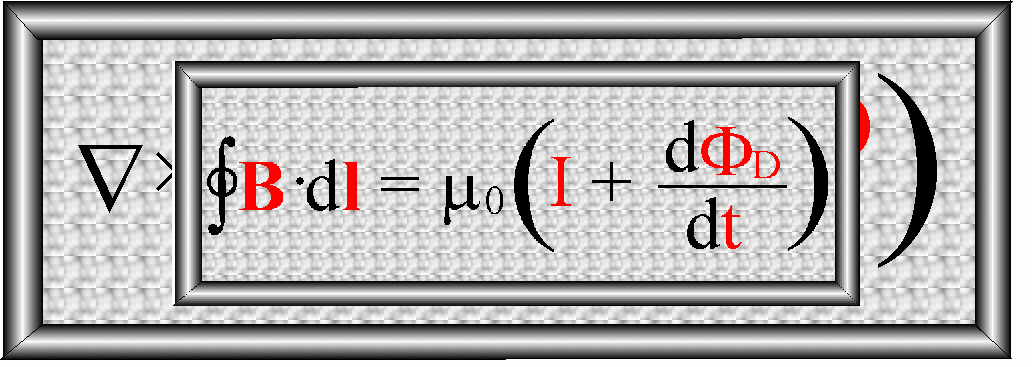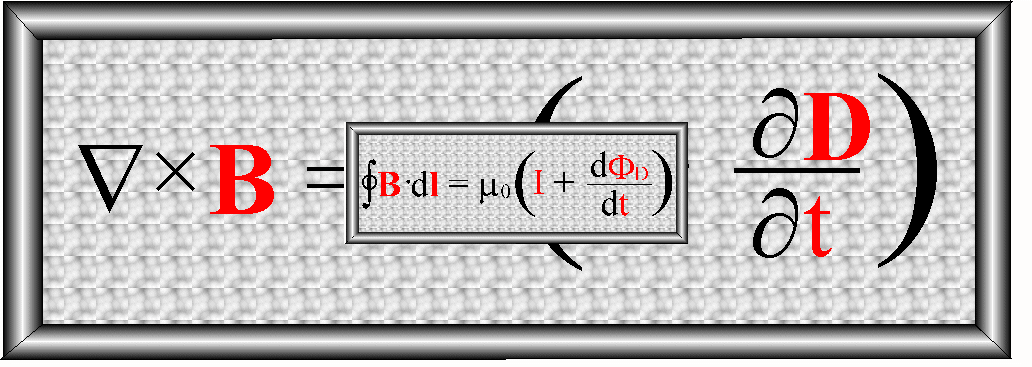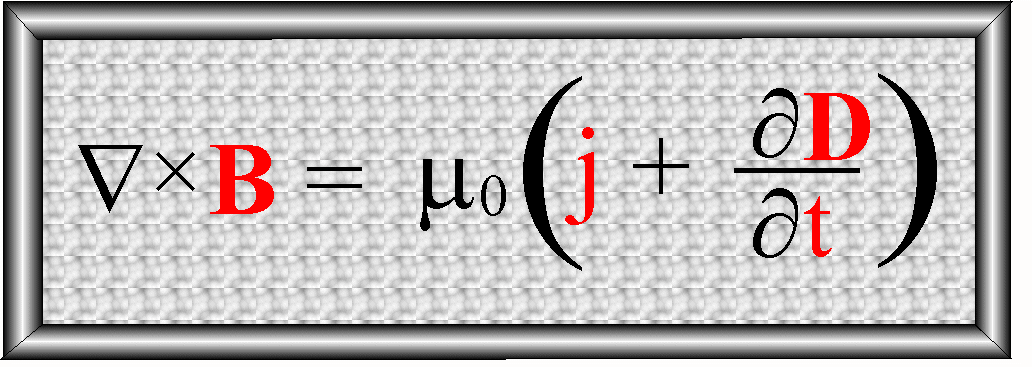
Prawo Gaussa dla pola elektrycznego – postać całkowa: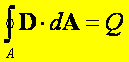

Na podstawie twierdzenia Gaussa – Ostrogradskiego zamieniamy całkę powierzchniową z lewej strony równania na całkę objętościową

Ładunek Q przedstawimy także jako całkę objętościową z gęstości ładunku ρ:

Z równości obu całek objętościowych

otrzymujemy prawo Gaussa dla pola elektrycznego – postać różniczkowa:

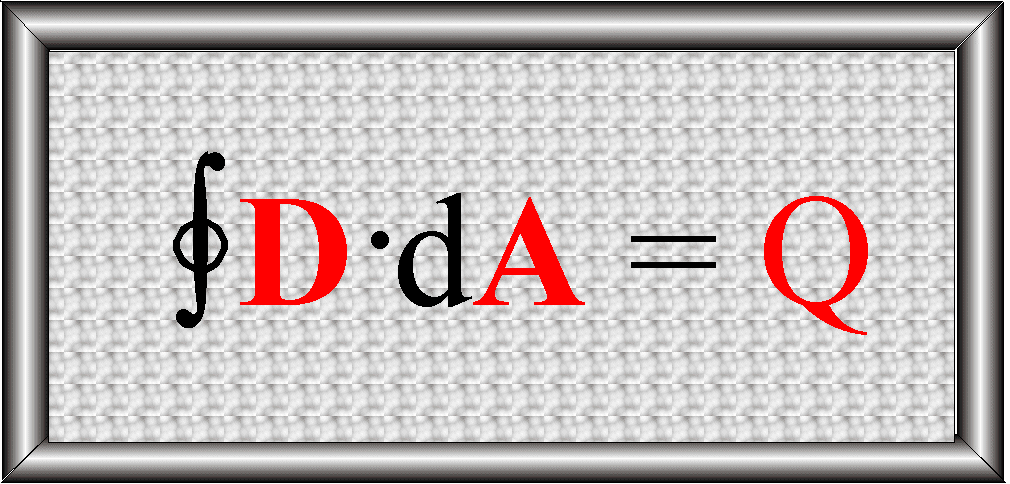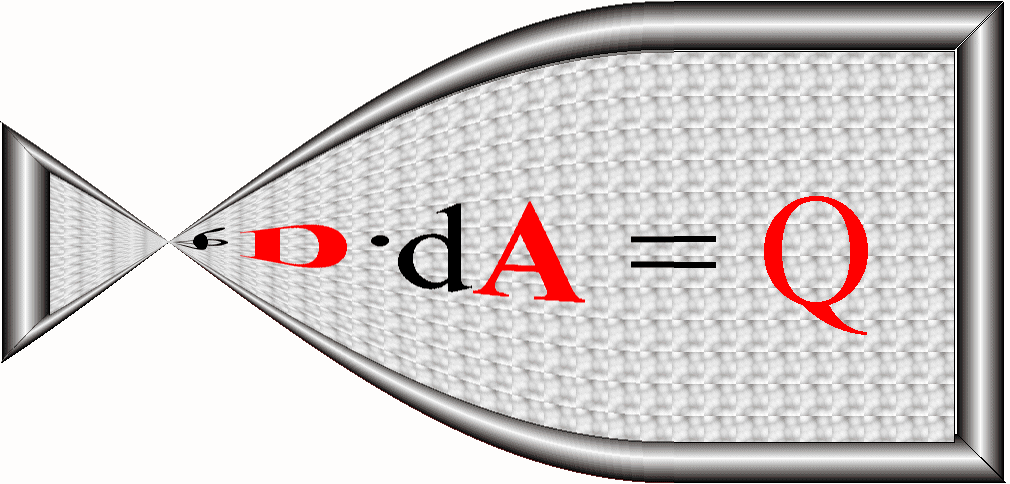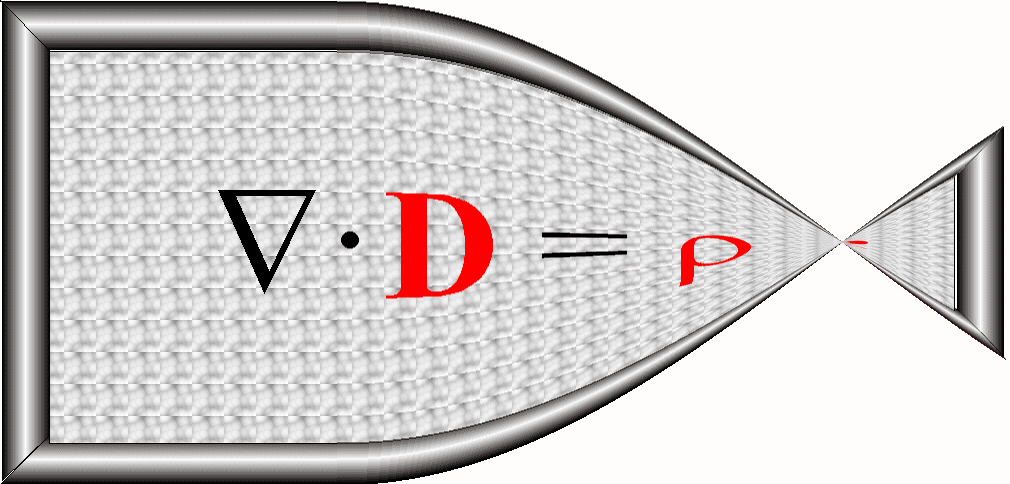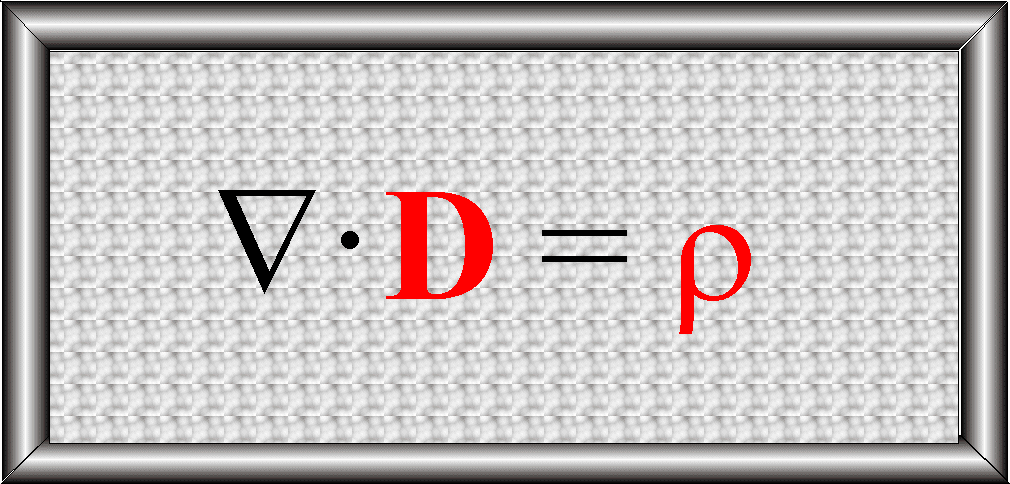
Prawo Gaussa dla pola magnetycznego – postać całkowa: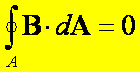

Na podstawie twierdzenia Gaussa – Ostrogradskiego zamieniamy całkę powierzchniową z lewej strony równania na całkę objętościową

Ponieważ na podstawie prawa Gaussa dla pola magnetycznego obie te całki równają się zeru, to i funkcje podcałkowe tez są równe zeru.. Stąd otrzymujemy od razu prawo Gaussa dla pola magnetycznego – postać różniczkowa:

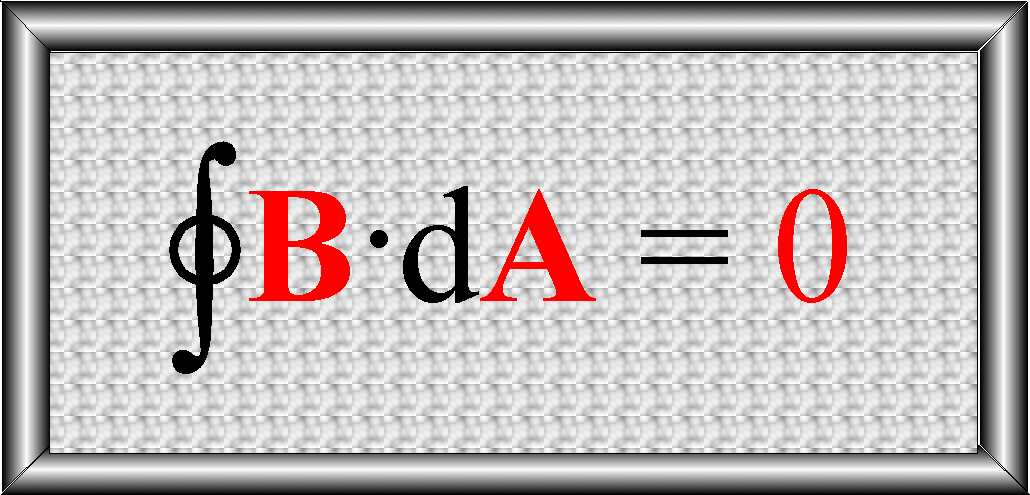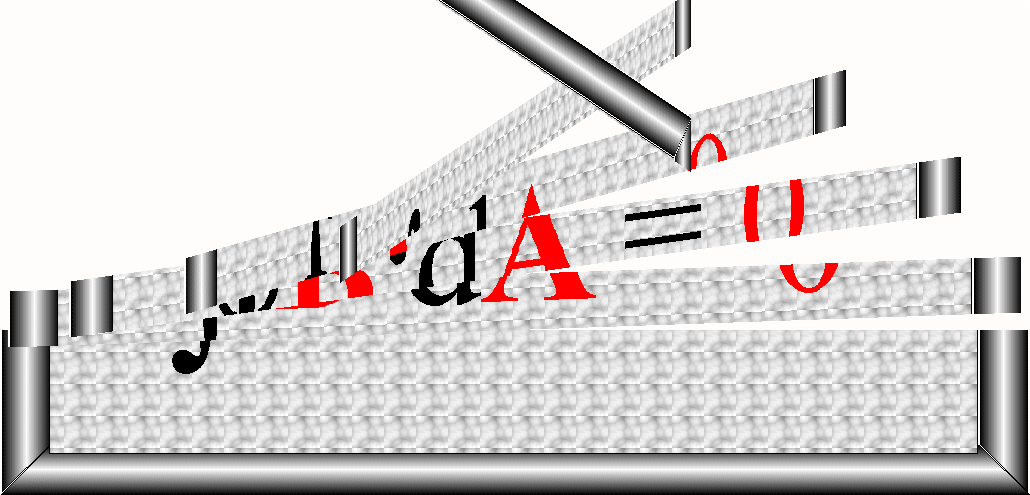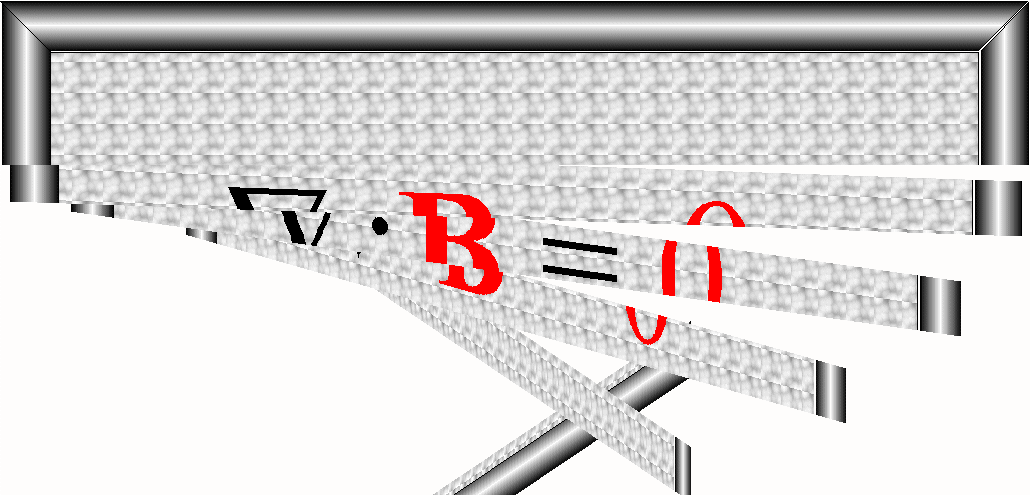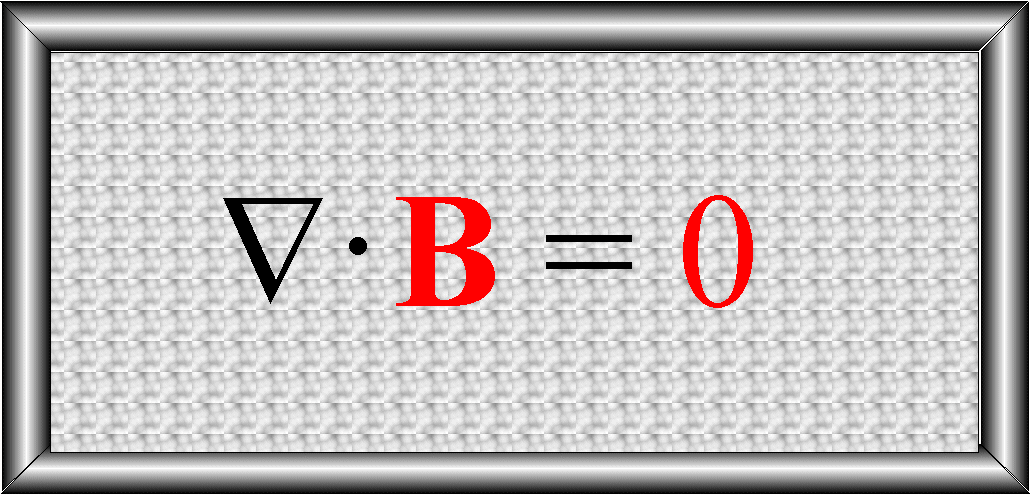
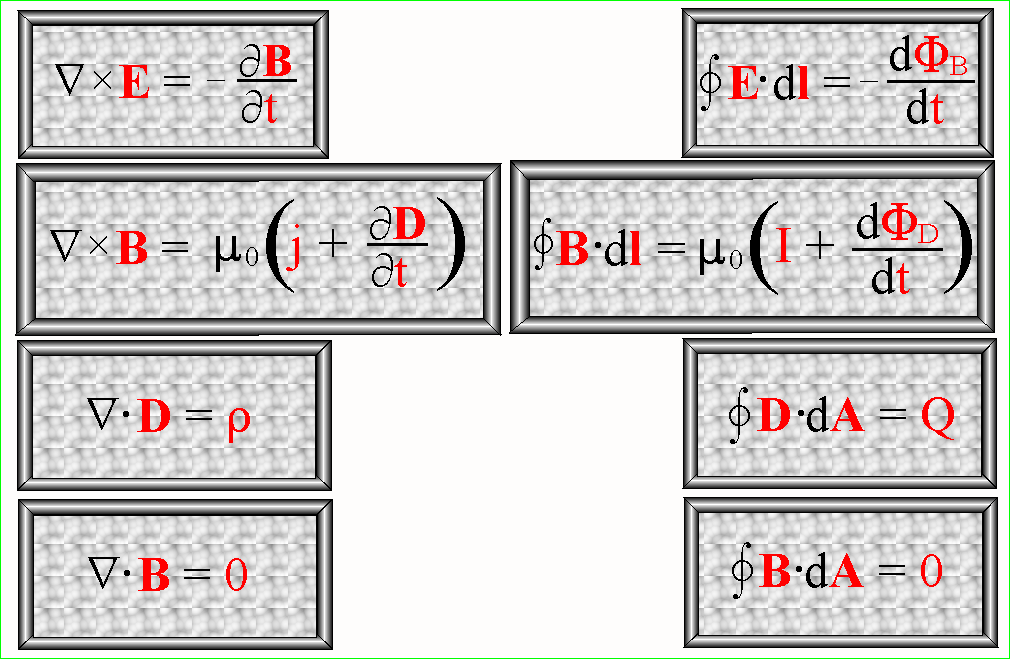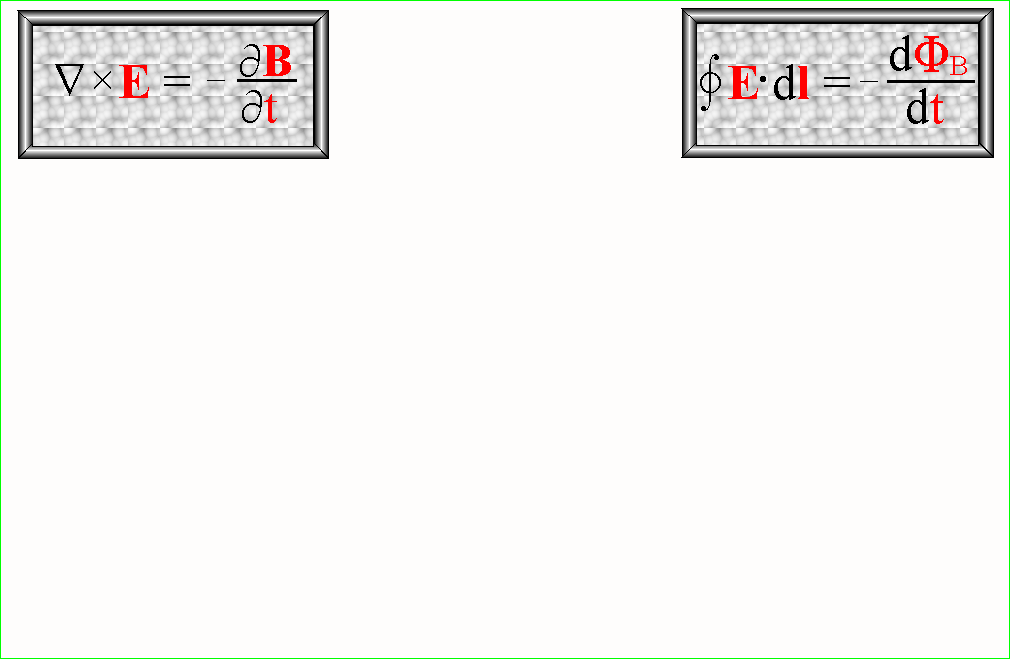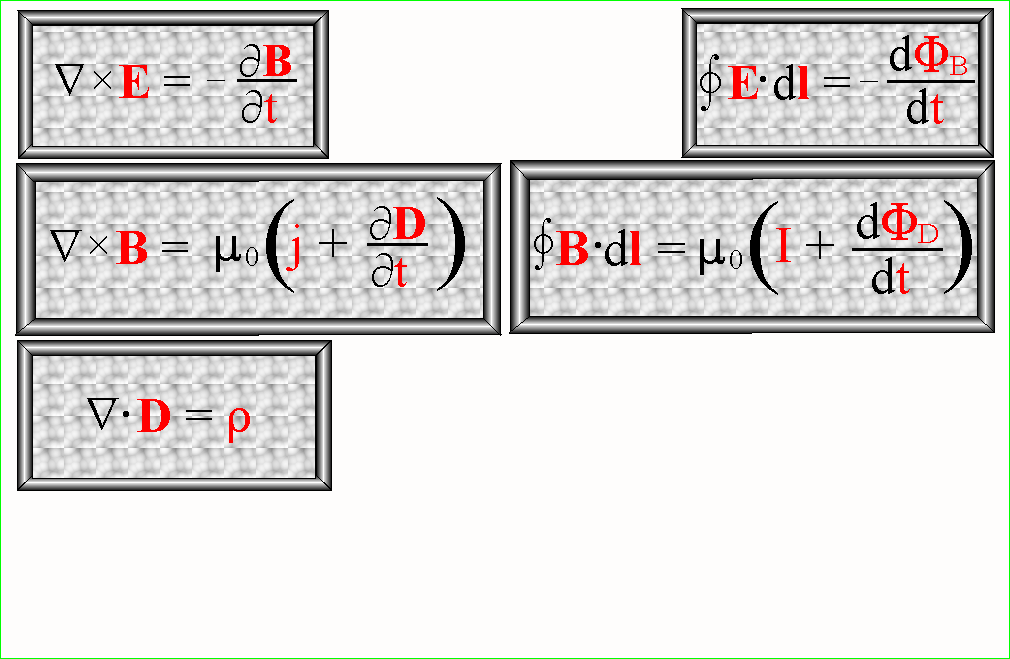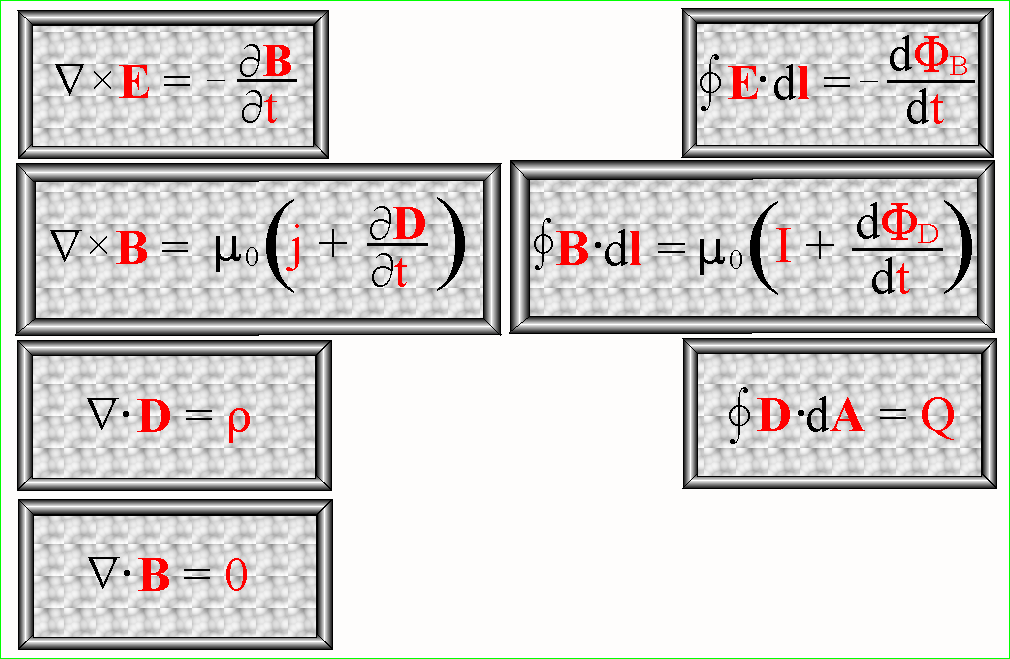
POSTAĆ RÓŻNICZKOWA POSTAĆ CAŁKOWA

Twierdzenie Gaussa-Ostrogradskiego

Twierdzenie Stokesa

Back to Index