Back to Index

TWIERDZENIE GAUSSA _ OSTROGRADSKIEGO I TWIERDZENIE STOKESA

* Twierdzenie Gaussa - Ostrogradskego

* Twierdzenie Stokesa

Otrzymane w poprzednich wykładach wspaniałe i zwarte równania Maxwella mają w elektrodynamice tak fundamentalne i głębokie znaczenie jak ma równanie 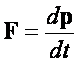w mechanice. Zostały te równania przedstawione w postaci całkowej, a teraz znajdziemy ich postać różniczkową konieczną dla lokalnego opisu pól elektrycznych i magnetycznych.

Równania Maxwella w postaci różniczkowej otrzymujemy w wyniku tylko przekształceń matematycznych równań w postaci całkowej. Oznacza to, że równania Maxwella w postaciach całkowej i różniczkowej są w zupełności równoważne względem siebie.

Do przekształceń równań Maxwella z jednej postaci do drugiej zastosujemy dwa twierdzenia matematyczne:

1. Twierdzenie Gaussa-Ostrogradskiego

2. Twierdzenie Stokesa

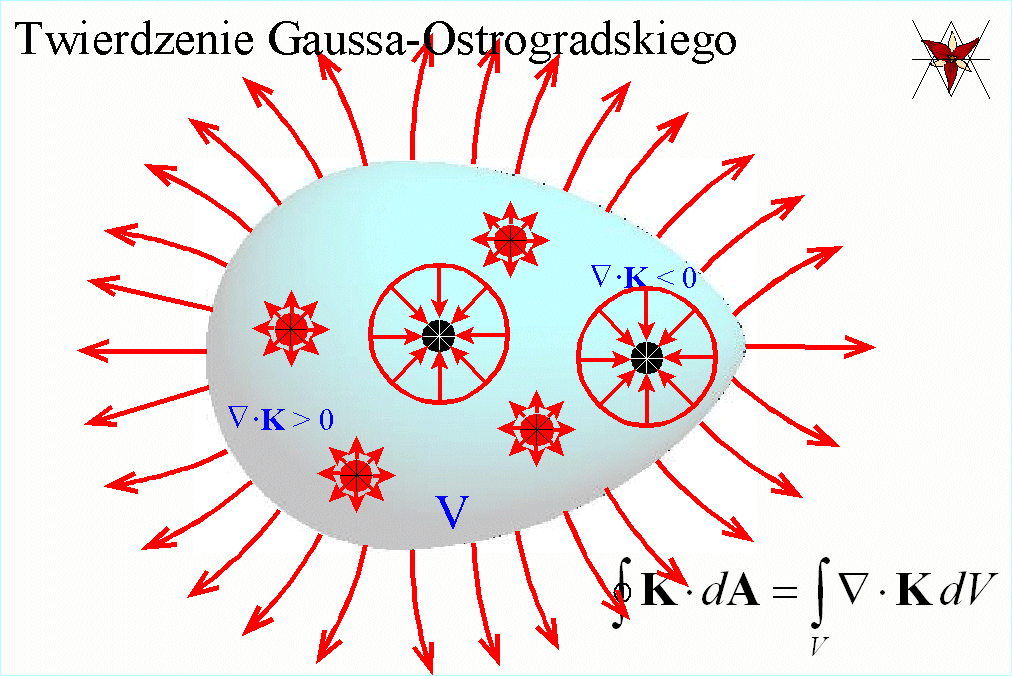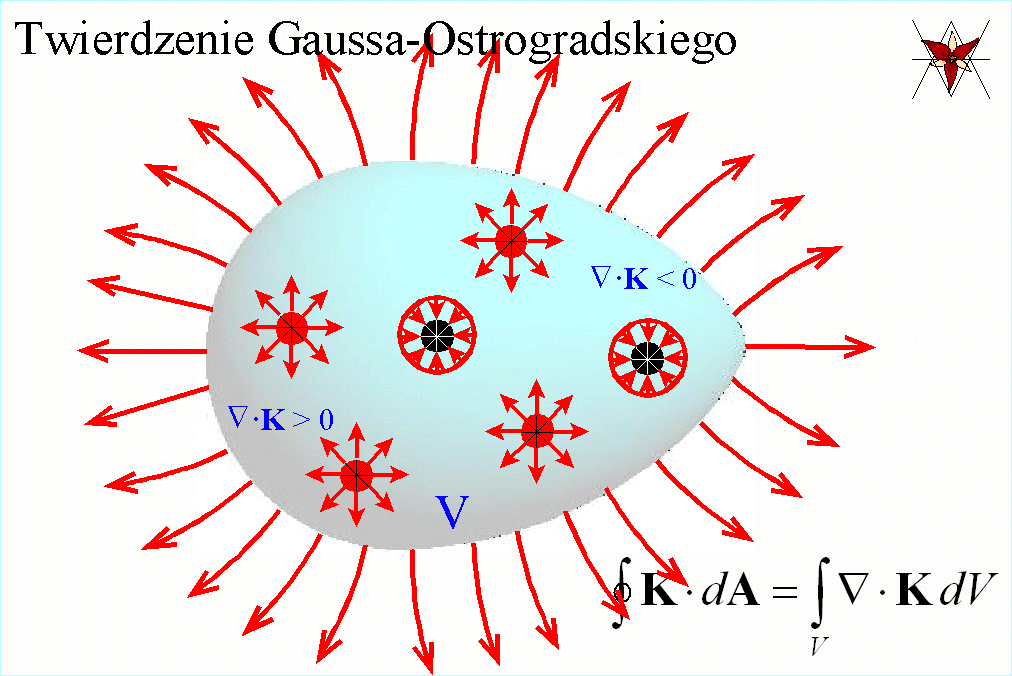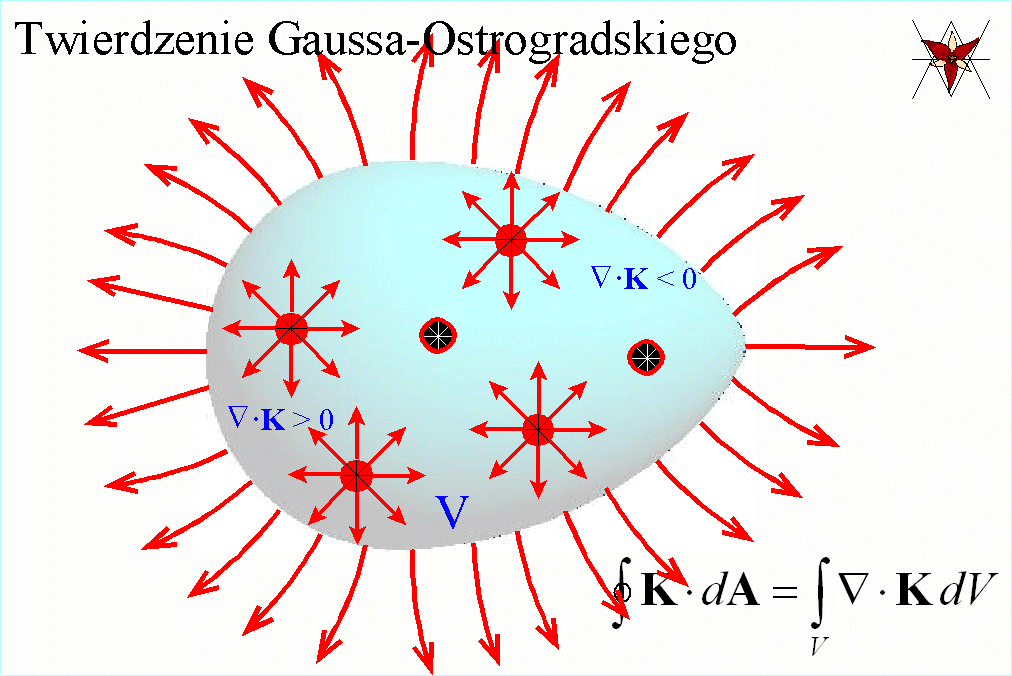
Twierdzenie Gaussa-Ostrogradskiego (twierdzenie o dywergencji) wiąże całkę powierzchniową dowolnej funkcji wektorowej K po zamkniętej powierzchni A z całką objętościową po objętości V ograniczonej powierzchnią A i orzeka, że strumień wektora K przez powierzchnię zamkniętą A jest równy całce objętościowej z dywergencji pola wektorowego K po objętości V ograniczonej powierzchnią A.

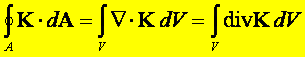
Najprościej mówiąc, twierdzenie to orzeka, że tym większy jest strumień 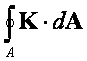pola K ,, przez powierzchnię zamkniętą A im większa jest wydajność (dywergencja) źródeł pola K, 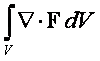, zawartych w objętości V ograniczonej powierzchnią zamkniętą A. Jeżeli wewnątrz powierzchni A będzie tyle samo punktów o dywergencji dodatniej (źródeł) co i punktów o dywergencji ujemnej (ścieków), to strumień pola K przez powierzchnię A będzie równy zeru.

Twierdzenie Stokesa (twierdzenie o rotacji) wiąże całkę liniową z funkcji wektorowej K po zamkniętym konturze L z całką powierzchniową po płacie powierzchniowym A ograniczonym przez kontur L i orzeka, że cyrkulacja wektora K po konturze L jest równa strumieniowi rotacji tego wektora przez płat A

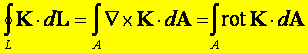
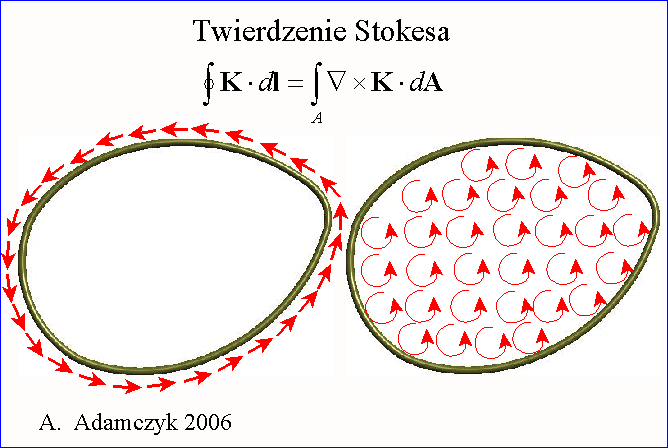
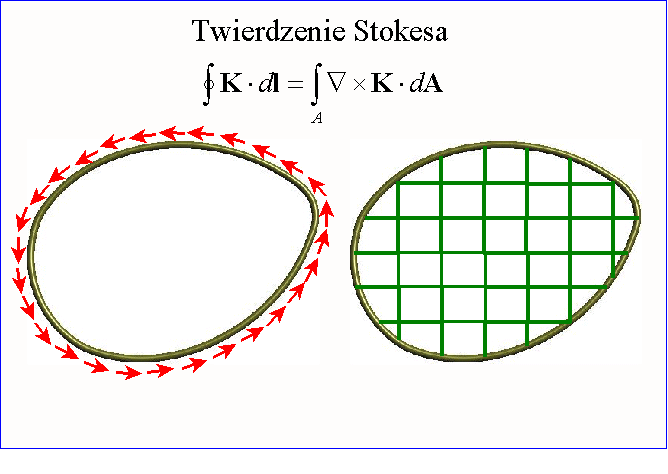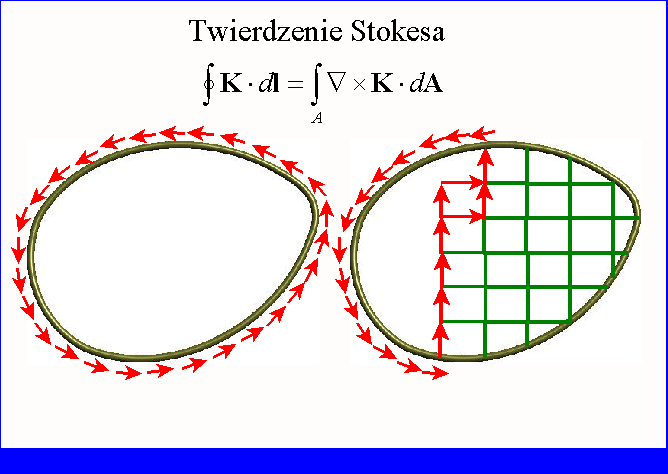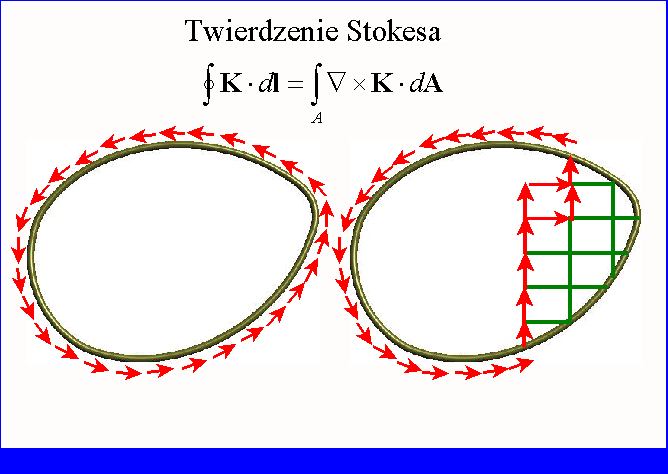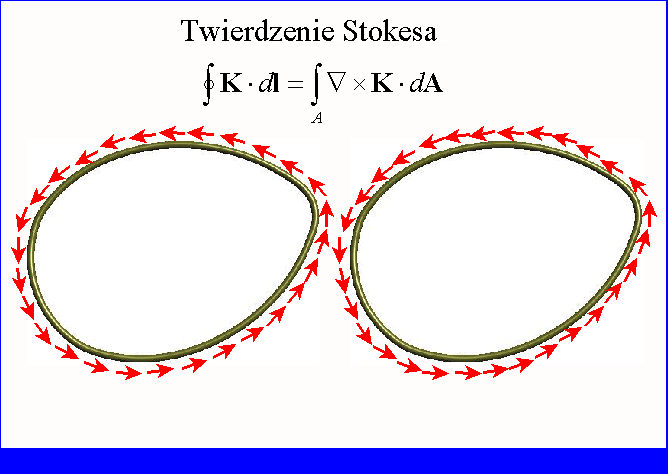
Aby to zobaczyć pokrywamy powierzchnię płata A siatką dowolnie małych konturów, np. siatką prostokątów, i obliczamy cyrkulację pola wektorowego K wzdłuż każdego z tych konturów. Im drobniejszą wybierzemy siatkę, tym cyrkulacja wektora K wzdłuż brzegów oczka siatki będzie dokładniej przybliżała wartość rotacji pola wektorowego K. Całkowanie w dwóch przeciwnych kierunkach wzdłuż sąsiadujących boków daje w rezultacie zero. Niezerowe pozostają tylko te wartości, które są wynikiem całkowania po fragmentach konturu ograniczającego płat A. Po zakończeniu takiego całkowania po całej powierzchni płata A otrzymujemy jedynie cyrkulację wektora K wzdłuż konturu ograniczającego ten płat. Jest to właśnie treścią twierdzenia Stokesa.

Opisane postępowanie jest zobrazowane w animacji poniżej.

Poznaliśmy już równania Maxwella w postaci całkowej. W następnym wykładzie zastosujemy twierdzenie Gaussa – Ostrogradskiego i twierdzenie Stokesa do otrzymywania równań Maxwella w postaci różniczkowej.

Back to Index