Back to Index

INDUKCJA ELEKTROMAGNETYCZNA

PRAWO FARADAYA. REGUŁA LENZA.

RÓWNANIA MAXWELLA W POSTACI CAŁKOWEJ.

* Indukcja elektromagnetyczna

* Prawo Faradaya

* Reguła Lenza

* Równania Maxwella w postaci całkowej

Istotą indukcji elektromagnetycznej jest zjawisko polegające na tym, że zmiana pola magnetycznego obejmującego obwód elektryczny powoduje powstanie siły elektromotorycznej w tym obwodzie, co w przypadku obwodu zamkniętego powoduje przepływ prądu elektrycznego. Jeżeli obwód, w którym mamy generować siłę elektromotoryczną, składa się z cewki i dołączonego do niej amperomierza, to źródłem zmieniającego się pola magnetycznego, które obejmuje cewkę, może być odpowiednio poruszany magnes stały albo poruszany elektromagnes lub elektromagnes, w którym zmieniamy prąd zasilający. W każdym z tych przypadków, lub im podobnych, pole magnetyczne przenikające cewkę zmienia się w czasie.

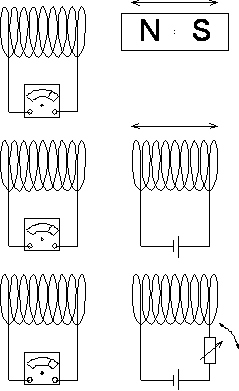
W ogólności, zmiana strumienia magnetycznego w obwodzie amperomierza indukuje prąd elektryczny w tym obwodzie.

Źródłem zjawisk indukcyjnych jest znowu siła Lorentza F pojawiająca się, gdy ładunek q porusza się z prędkością v w polu magnetycznym B

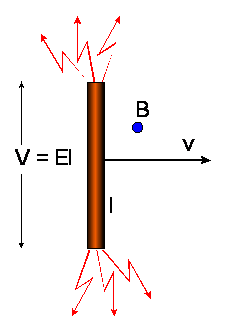
Gdy przewodnik przesuwamy w polu B, to ruchome nośniki ładunku zostaną przesunięte pod działaniem siły Lorentza tak daleko aż pojawi się w przewodniku pole elektryczne E i siła działająca na nośniki F = qE zrównoważy siłę Lorentza. Kiedy prostoliniowy przewodnik o długości l porusza się z jednostajną prędkością v w jednorodnym polu magnetycznym B skierowanym prostopadle do osi przewodnika i do wektora prędkości v, jak na rysunku

wtedy warunek równowagi między siłą Lorentza a siłą odpychania między ładunkami zapiszemy w postaci równania

Stąd

gdzie V jest różnicą potencjałów na końcach przewodnika o długości l. Wartość tej różnicy potencjałów wynosi zatem

Jeżeli wektor v nie jest prostopadły do pola B , ale tworzy z nim kąt N, wtedy różnica potencjałów na końcach przewodnika wyniesie

co oznacza, że przesuwanie przewodnika wzdłuż kierunku pola B nie będzie generowało w nim siły elektromotorycznej. Łatwo dowieść, że w przypadku przewodnika o dowolnym kształcie, różnica potencjałów między punktami a i b przewodnika jest równa

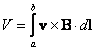
Kiedy prostokątna ramka o bokach a i b obraca się w jednorodnym polu magnetycznym B ze stałą prędkością kątową T.

to siła elektromotoryczna V generowana w obydwu bokach ramki o długości a wyniesie

Siły magnetyczne działające w dwóch pozostałych bokach pętli są do tych boków prostopadłe i nie wnoszą udziału do siły elektromotorycznej. Przez odpowiedni sposób odbioru generowanego napięcia można zrealizować najprostsze modele prądnic prądu zmiennego (a) i stałego (b), jak pokazano na rysunku

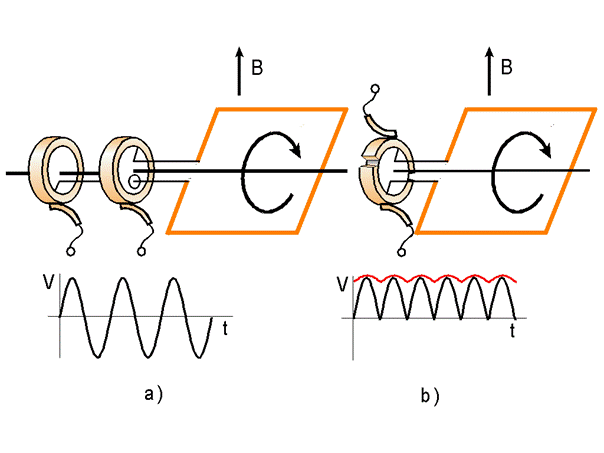
W przyrodzie i technice występuje ogromna ilość zjawisk, których przyczyną jest indukcja elektromagnetyczna, czyli generowanie siły elektromotorycznej w przestrzeni gdzie występuje zmieniające się pole magnetyczne. Wszystkie te zjawiska są opisywane jednym wspaniałym, zwartym równaniem będącym treścią prawa Faradaya.

Wspaniałym odkryciem Michaela Faradaya (1791 – 1867) było znalezienie reguł rządzących indukcją elektromagnetyczną. W rezultacie wieloletnich eksperymentów Faraday stwierdził, że siła elektromotoryczna E pojawia się w przewodniku gdy otaczające ten przewodnik pole magnetyczne ulega zmianie, wartość generowanej siły elektromotorycznej jest proporcjonalna do szybkości zmian pola magnetycznego oraz że kierunek indukowanej siły elektromotorycznej zależy od kierunku, w którym następują zmiany pola magnetycznego. Wszystkie te fakty są zawarte w jednym tylko równaniu

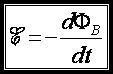
gdzie dΦ_B jest elementarnym strumieniem pola magnetycznego

W ogólnym przypadku, nawet wtedy, gdy nie ma żadnych przewodników, siła elektromotoryczna jest równa cyrkulacji pola elektrycznego E wzdłuż konturu zamkniętego

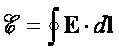
Zatem prawo Faradaya można zapisać w postaci uogólnionej

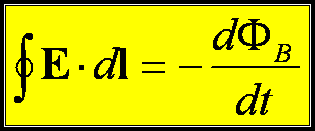
Proszę zwrócić uwagę na ile sposobów może zmieniać się wartość strumienia :

1. Przez zmianę wartości wektora B;

2. Przez zmianę wartości pola powierzchni dA;

3. Przez zmianę kąta między B i dA;

4. Przez jednoczesną zmianę B i dA;

5. Przez jednoczesną zmianę B i kąta;

6. Przez jednoczesną zmianę dA i kąta.

Nie można przeoczyć znaku minus, który się tutaj pojawił! Ten znak minus w prawie Faradaya został nazwany regułą Lenza, którą możemy rozumieć jako regułę przekory w elektrodynamice.

Reguła Lenza (znak minus w prawie Faradaya) ustala, że kierunek prądu indukowanego w procesie indukcji elektromagnetycznej jest taki, aby własne pole magnetyczne tego prądu miało taki kierunek zmian, który przeciwdziała zmianom pola indukującego. aby osłabiać pole narastające ale wzmacniać pole słabnące. Prawo indukcji Faraday’a łącznie z regułą Lenza przedstawia animacja:, w której przesuwanie magnesu stałego powoduje powstanie siły elektromotorycznej w cewce obejmowanej przez pole magnesu.

Kiedy magnes pozostaje nieruchomy w swoich skrajnych położeniach wtedy żadna siła elektromotoryczna nie jest generowana i miernik nie wychyla się ani w prawo ani lewo. W czasie zbliżania magnesu w cewce płynie prąd indukcyjny o takim kierunku, aby powstający elektromagnes był skierowany swoim biegunem N w kierunku bieguna N zbliżanego magnesu stałego (hamowanie zbliżania). W czasie oddalania magnesu kierunek prądu indukcyjnego ulega odwróceniu i teraz powstający elektromagnes ma swój biegun S skierowany ku biegunowi N oddalanego magnesu stałego (hamowanie oddalania).

Prąd indukcyjny może powstawać nie tylko w uzwojeniach, ale także w litych blokach metalowych umieszczonych w zmieniających się polach magnetycznych.

. Przykładem są tzw. prądy wirowe, jak przedstawione schematyczne na rysunku:, które mogą spełniać pożyteczną rolę.

Kiedy do obracającej się aluminiowej tarczy przyłożymy prostopadłe do niej stałe pole magnetyczne (symbolizowane przez czerwone kółko) wtedy w tarczy zostają wytworzone dwie rodziny przeciwnie skierowanych wirów prądowych . Pole magnetyczne prądów wirowych jest tak skierowane, że ta część tarczy, która wychodzi z pola będzie z powrotem wciągana do pola natomiast ta część tarczy, która wchodzi w obszar pola będzie z tego pola wypychana.

Prądy wirowe są często niepożądane, jak np. w rdzeniach transformatorów, w których powodują straty na wytwarzanie ciepła. Aby ograniczyć prądy wirowe rdzenie transformatorów wykonuje się w postaci stosów kształtek blaszanych.

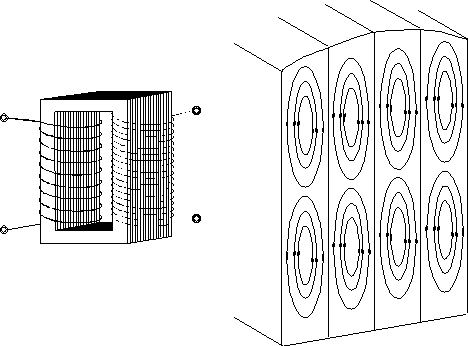
Redukcja prądów wirowych przez zastosowanie rdzenia warstwowego.

Prawo Faradaya wchodzi wraz z uogólnionym prawem Ampera oraz prawem Gaussa dla pola elektrycznego i prawem Gaussa dla pola magnetycznego w zestaw czterech równań Maxwella. Równania te zostały dotychczas przedstawione w odniesieniu do makroskopowych konturów i powierzchni zamkniętych. Z tego powodu mówimy, że są to równania Maxwella w postaci całkowej. Spójrzmy jeszcze raz na te równania. Są to:

Prawo Faradaya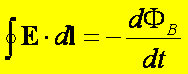

Uogólnione prawo Ampera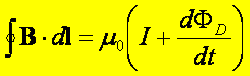

Prawo Gaussa dla pola elektrycznego

Prawo Gaussa dla pola magnetycznego

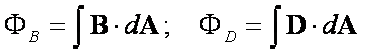
Całkowe równania Maxwella opisują zjawiska elektryczne i magnetyczne w skali makroskopowej. Do ich sformułowania potrzebne są przecież kontury, powierzchnie zamknięte, prądy i strumienie pól. Niezwykle ważne jest jednak wiedzieć co dzieje się z polami elektrycznymi i magnetycznymi w pojedynczych punktach czyli w skali mikroskopowej. Wtedy dopiero będzie można opisywać takie zjawiska jak fale elektromagnetyczne.

Do opisu mikroskopowego zjawisk elektrycznych i magnetycznych służą równania Maxwella w postaci różniczkowej. Aby je otrzymać zastosujemy do równań w postaci całkowej dwa twierdzenia matematyczne: twierdzenie Gaussa-Ostrogradskiego i twierdzenie Stokesa.

Należy zauważyć, że przekształcanie równań Maxwella między postaciami całkową i różniczkową otrzymujemy w wyniku tylko zabiegów matematycznych. Oznacza to równoważność fizyczną tych dwóch postaci równań Maxwella.

Twierdzenie Gaussa-Ostrogradskiego i twierdzenie Stokesa, mimo pozornej złożoności, są koncepcyjnie zupełnie proste i łatwe do intuicyjnego zaakceptowania. Oba te twierdzenia zostaną przedstawione w następnym wykładzie.

Back to Index