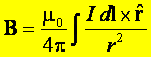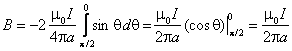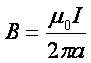Back to Index

PRAWO AMPERE’A

ZASTOSOWANIE PRAWA AMPERE’A DO OBLICZANIA PÓL MAGNETYCZNYCH PRĄDÓW

* Prawo Ampere’a

* Pole B wokół przewodnika prostoliniowego – porównanie zastosowania prawa Biota i Savarta oraz prawa Ampere’a

* Inne zastosowania prawa Ampere’a do obliczania pól magnetycznych prądów

Podobnie jak prawo Biota i Savarta, również prawo Ampere’a określa relację między polem magnetycznym i prądem elektrycznym, który wytwarza

to pole. W wielu sytuacjach stosowanie prawa Ampere’a powoduje, że obliczenia stają się znacznie prostsze i wygodniejsze od przeprowadzonych za pomocą prawa Biota i Savarta.

Matematycznie prawo Ampere’a jest równaniem wiążącym cyrkulację wektora magnetycznego B czyli całkę wziętą wzdłuż zamkniętego płaskiego konturu L (na oznaczenie elementu konturu używamy dL, zaś elementu przewodnika dl )

Jeżeli kontur L obejmuje kilka przewodników z prądami, to te prądy dodajemy do siebie, gdy wszystkie one przecinają płaszczyznę konturu od tej samej strony. Jeżeli niektóre z tych prądów przecinają płaszczyznę konturu od przeciwnej strony to takie prądy są odejmowane, jak pokazano na prawym rysunku.

Prawo Ampere’a orzeka, że

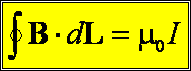
gdzie μ₀ jest przenikalnością magnetyczną próżni. Można to prawo wyrazić słownie:

cyrkulacja wektora B wzdłuż zamkniętego płaskiego konturu L jest równa iloczynowi μ₀ i całkowitego prądu I przecinającego powierzchnię ograniczoną tym konturem.

Prawo Ampere’a, podobnie jak prawa dynamiki Newtona i prawa (zasady) termodynamiki, nie może zostać wyprowadzone z jeszcze prostszych praw przyrody. Każde z nich jest odgadnięte na podstawie obserwacji i analizy zjawisk, a zatem jest rezultatem olśnienia, jakiego doznał twórca, który je znalazł. Wierzymy, że te prawa są uniwersalne i obowiązują jednakowo w całym Wszechświecie i jesteśmy przekonani, że nigdzie nie znajdziemy zjawiska, które złamałoby to prawo.

Prawo Ampere’a w przedstawionej teraz postaci jest bardzo użyteczne, ale ciągle pozostaje jeszcze bombą bez wkręconego zapalnika. Takim zapalnikiem, który wyzwala pełną moc prawa Ampere’a, jest pole magnetyczne prądu przesunięcia dodane przez Maxwella. Dzięki tej genialnej idei Maxwella, prawo Ampere’a zostało uogólnione i należy do zestawu czterech równań Maxwella, które teraz opisują wszystkie zjawiska elektryczne i magnetyczne, ale także przewidują powstawanie fal elektromagnetycznych i opisują rozchodzenie się tych fal. Dzięki temu równania Maxwella opisują także zjawiska optyczne.

Uogólnione prawo Ampere’a zostanie przedstawione w następnym wykładzie.

Obliczanie pola B wokół przewodnika prostoliniowego
Wykorzystanie prawa Biota i Savarta	Wykorzystanie prawa Ampere’a
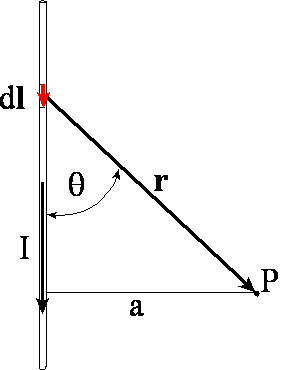
Pole magnetyczne długiego prostoliniowego przewodnika z prądem można wyliczyć stosując prawo Biota i Savarta: Pole dB odcinka z prądem o długości dl w punkcie P (w odległości a od osi przewodnika) wynosi Aby uzależnić dB tylko od kąta θ zastosujemy podstawienia: Mamy teraz Po scałkowaniu po całej (nieskończonej) długości przewodnika otrzymujemy Zatem w odległości a od osi przewodnika prostoliniowego wartość pola B wynosi	Pole magnetyczne długiego prostoliniowego przewodnika z prądem można wyliczyć bardzo prosto (pamięciowo) stosując prawo Ampere’a: Przewodnik z prądem otaczamy płaskim konturem L o kształcie okręgu leżącym w płaszczyźnie prostopadłej do przewodnika. Przewodnik przechodzi przez środek okręgu. Kontur L dzielimy na nieskończenie małe odcinki dL. z których każdy jest równoległy do lokalnego kierunku pola B Z tego powodu iloczyn skalarny pod znakiem całki zostaje zamieniony na zwykły iloczyn BdL, przy czym wartość B jest stała i może zostać wyniesiona przed znak całki. Otrzymujemy stąd równanie Zatem w każdym punkcie okręgu o promieniu a wokół przewodnika prostoliniowego wartość pola B jest dana przez wyrażenie, które już otrzymaliśmy przez pracochłonne całkowanie na podstawie prawa Biota i Savarta.

1. Znaleźć pole magnetyczne B wewnątrz i na zewnątrz długiego przewodnika o kształcie walca, przez który płynie prąd o natężeniu I.

Jeżeli promień walca wynosi R, to wewnątrz walca w odległości r < R od jego osi znajdujemy rysując kontur L w kształcie okręgu o promieniu r tak, że płaszczyzna konturu jest prostopadła do osi walca a środek konturu znajduje się na osi walca. Symetria takiej konstrukcji powoduje, że wartość pola B jest stała w każdym punkcie konturu a wektor B jest wszędzie styczny do konturu (równoległy do elementu dL). Obliczając całkę

uwzględniamy fakt, że o wartości pola B decyduje tylko ten prąd I_r, który płynie wewnątrz konturu L o promieniu r. Stosunek wartości prądu I_r do wartości całkowitego prądu I płynącego przez przewodnik walcowy jest taki sam jak stosunek powierzchni ograniczonej konturem L do powierzchni przekroju poprzecznego walca, czyli

Stąd otrzymujemy

Po scałkowaniu mamy

czyli wewnątrz przewodnika pole B rośnie liniowo wraz ze wzrostem r

Na zewnątrz przewodnika, gdy r > R, pole B maleje hiperbolicznie jak wokół prostego przewodnika

Przebieg pola B wewnątrz i na zewnątrz walca jest pokazany na dolnym rysunku.

2. Znaleźć wartość pola B na osi solenoidu zawierającego N zwojów, przez który płynie prąd I. .

Tutaj właściwym konturem L będzie prostokąt jak przedstawiony na rysunku. Przyjmujemy, że wartość pola B jest równa zeru na zewnątrz ściany uzwojenia. Pionowe boki prostokąta są prostopadłe do wektora B, a zatem iloczyn skalarny B·dL jest na tych bokach równy zeru. W ten sposób całkowanie w prawie Ampere’a redukuje się do zwykłej całki wzdłuż boku leżącego na osi solenoidu.

Otrzymujemy zatem

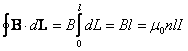
Ponieważ pole konturu jest przecinane przez nl zwojów, gdzie n jest ilością zwojów na jednostkę długości uzwojenia, to prąd I w prawie Ampere’a musimy zwiększyć n-krotnie. W wyniku dostajemy

3. Znaleźć wartość pola B na osi solenoidu toroidalnego zawierającego N zwojów, przez który płynie prąd I.

Zadanie rozwiązujemy analogicznie, jak poprzednie tyle, że właściwym konturem L będzie tutaj okrąg leżący jak przedstawiono na rysunku.

W każdym punkcie konturu wektor B jest równoległy do wektora dL i całkowanie w prawie Ampere’a staje się bardzo proste

Stąd otrzymujemy, że

Również i tutaj n oznacza ilość zwojów na jednostkę długości uzwojenia.

Back to Index