Back to Index

ŹRÓDŁA POLA MAGNETYCZNEGO:

POLE MAGNETYCZNE ŁADUNKU W RUCHU JEDNOSTAJNYM.

POLE B ODCINKA Z PRĄDEM.

PRAWO Biota i Savarta.

* Pole magnetyczne ładunku w ruchu jednostajnym

* Pole B odcinka z prądem

* Prawo Biota i Savarta

Przejdziemy teraz do zasad opisujących sposób powstawania pola magnetycznego w otoczeniu poruszających się ładunków i prądów elektrycznych. Najbardziej podstawową zależnością jest prawo opisujące wartość i kierunek pola magnetycznego wytwarzanego przez poruszający się pojedynczy ładunek punktowy. To prawo zostanie wykorzystane później do otrzymania prawa Biota i Savarta, prawa Ampere’a, prawa Gaussa dla pola magnetycznego i tworzy użyteczne alternatywne sformułowanie relacji między polami magnetycznymi a ich źródłami.

EXPERYMENTALNIE POKAZANO, że wartość B jest ponownie proporcjonalna do q oraz do 1/r². Jednak kierunek wektora B NIE leży na prostej między źródłem punktowym a punktem pola. Jest on natomiast prostopadły do płaszczyzny wyznaczonej przez tę prostą i przez wektor prędkości ładunku v. Ponadto, wartość pola jest proporcjonalna do sinusa kąta między tymi dwoma kierunkami

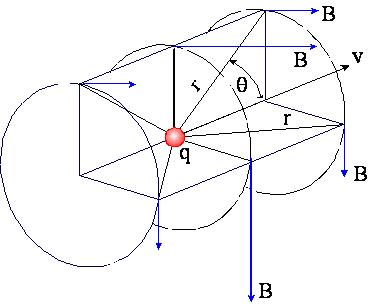
Tę zależność możemy napisać w sposób bardziej zwarty przez zastosowanie iloczynu wektorowego wektora v i wektora jednostkowego . Otrzymujemy stąd ostateczne wyrażenie na pole B w postaci

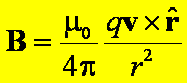
μ₀ jest przenikalnością magnetyczną próżni, która ma wartość

Kiedy zmieniamy kąt obserwacji pola B przy ustalonej odległości R od poruszającego się ładunku wtedy zachodzące zmiany można przedstawić jak w animacji:

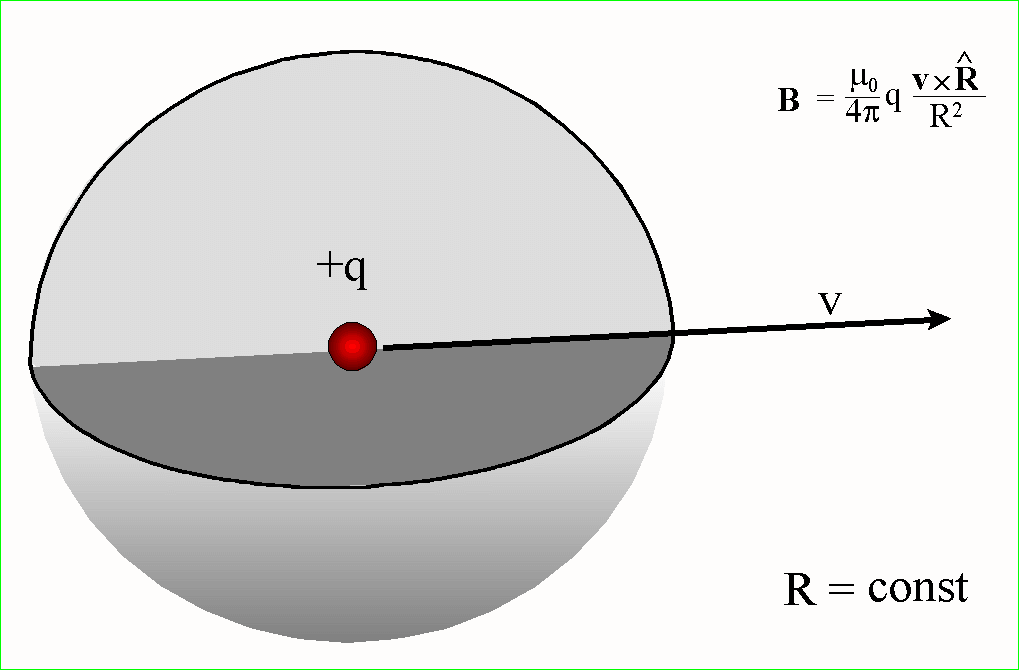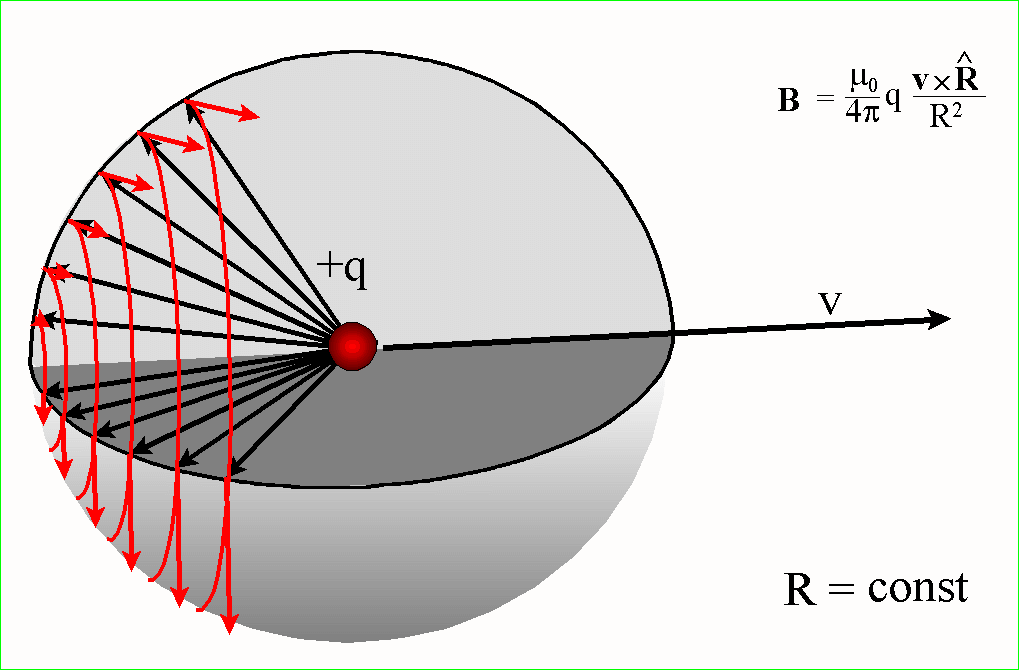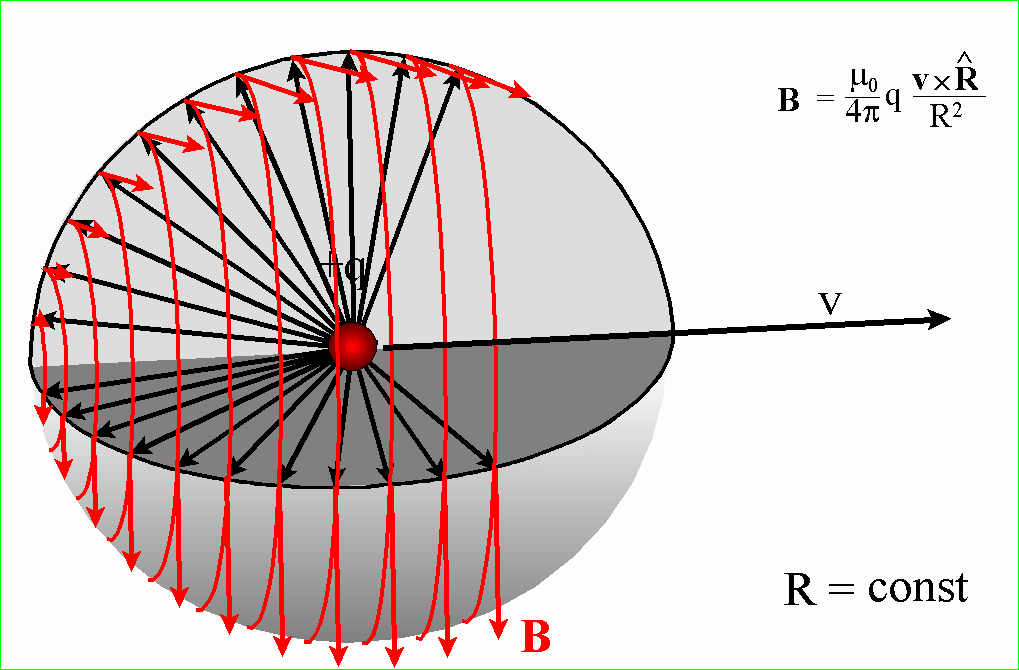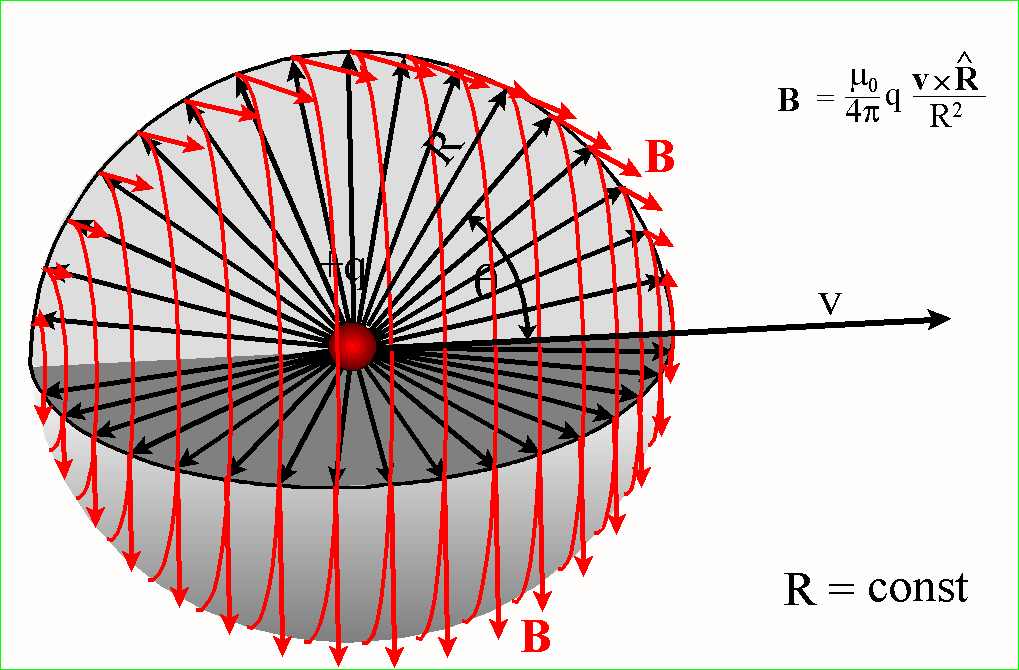
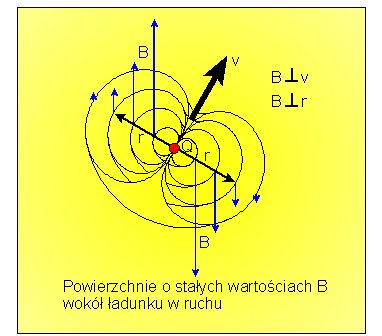
Powierzchnie o jednakowej wartości i kierunku pola B wokół poruszającego się ładunku można przedstawić jako układ współosiowych muszli

Oczywiście, nie ma znaczenia czy porusza się ładunek względem obserwatora, czy obserwator względem ładunku. Naelektryzowany kot wytwarza pole magnetyczne B, kiedy przechodzi koło ciebie, ale też, gdy ty przechodzisz obok śpiącego kota.

Powierzchnie o stałej wartości B można przedstawić bardziej plastycznie, jak w animacji poniżej

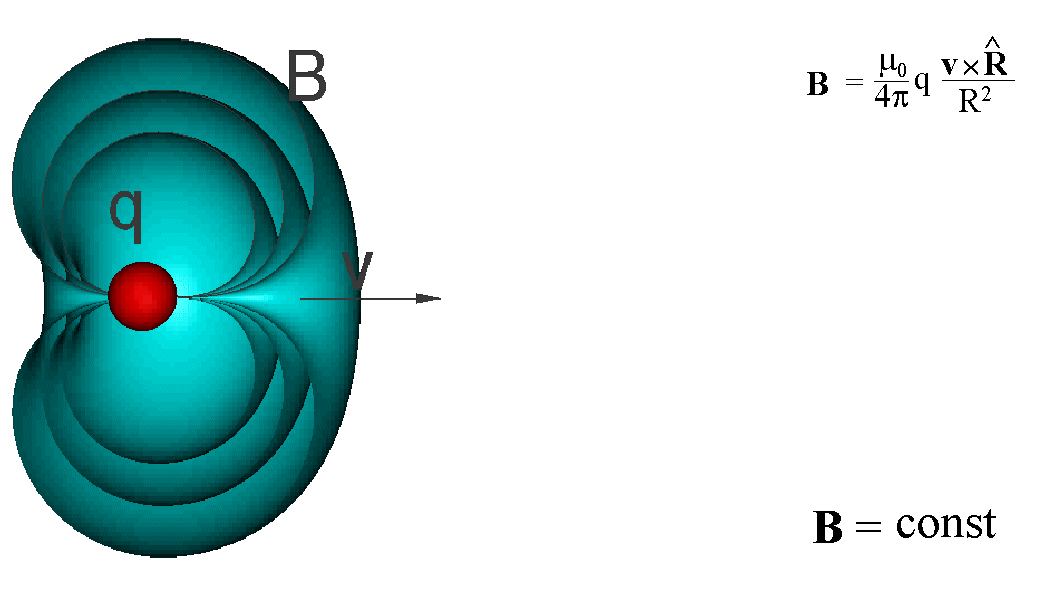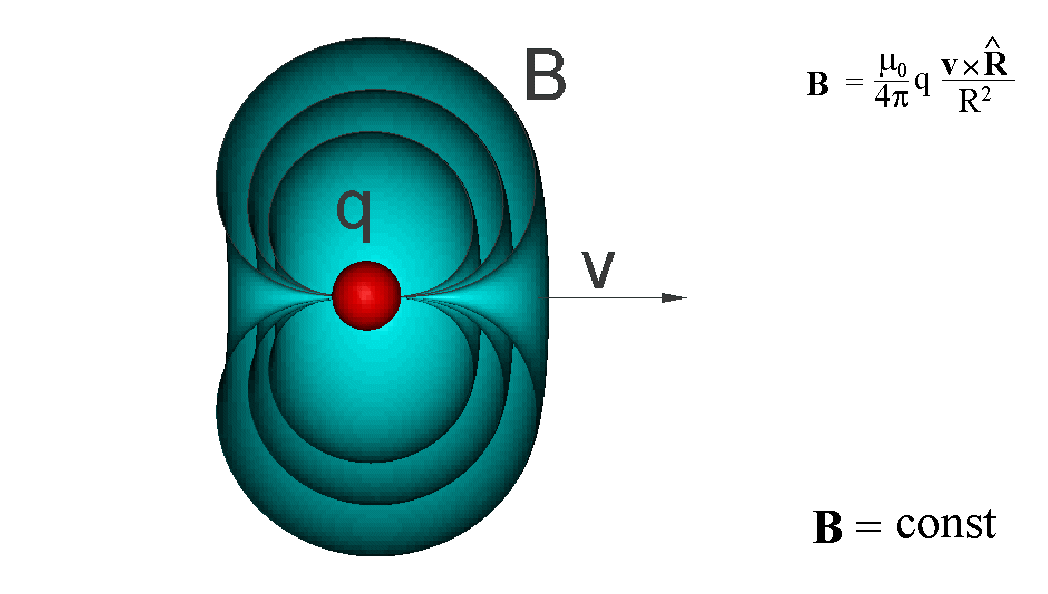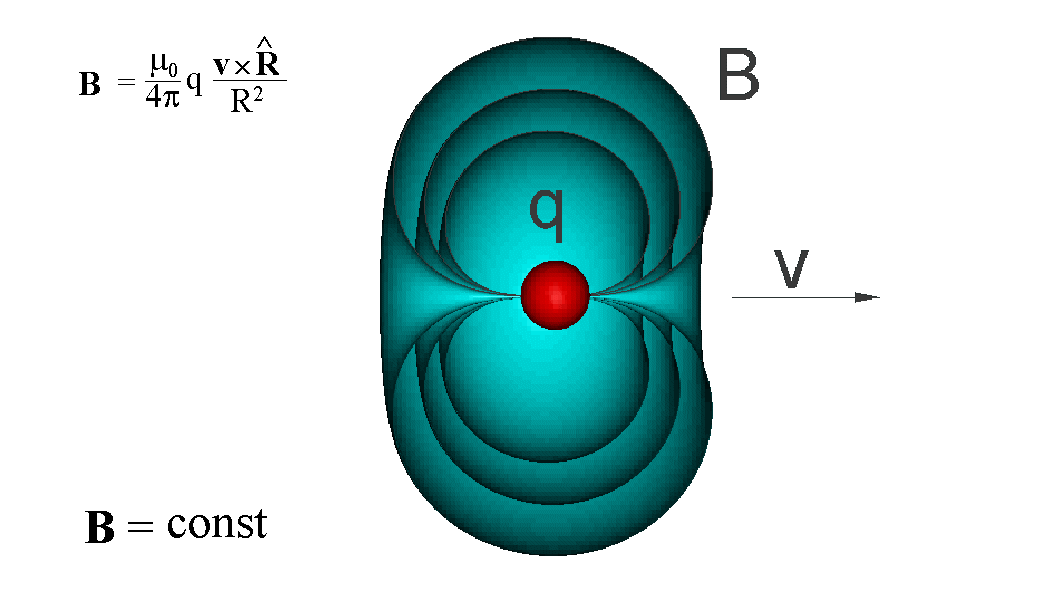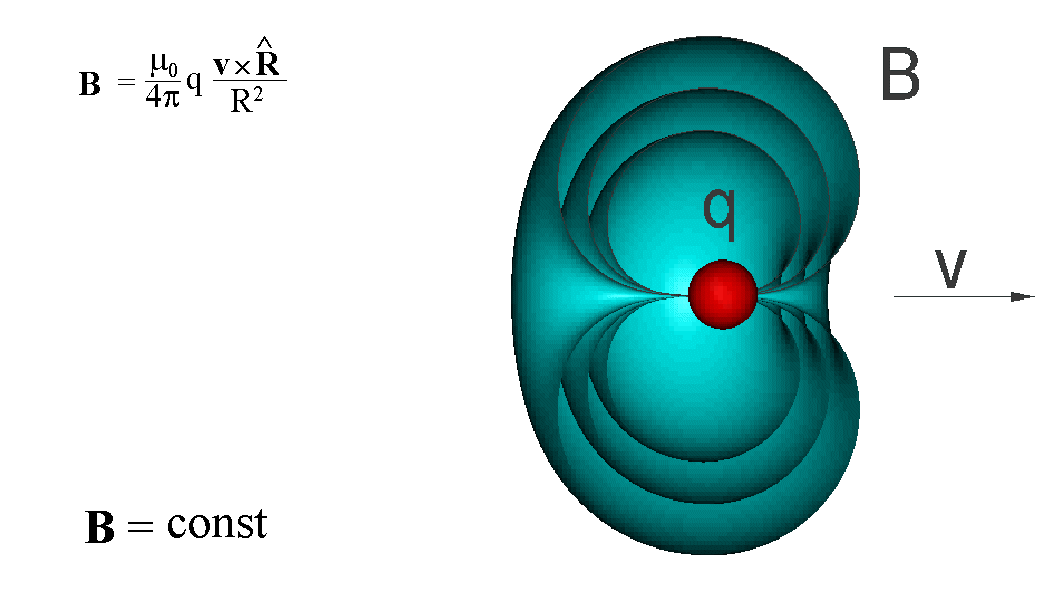
Na zakończenie możemy napisać wyrażenie na siłę magnetyczną F działającą między dwoma ładunkami punktowymi poruszającymi się względem obserwatora z prędkościami v i v’. Ponieważ siła F będzie siłą Lorentza, w której pole B pochodzi od ładunku w ruchu to możemy napisać

Zatem poszukiwana siła jest wyrażona przez równanie

gdzie r jest odległością między oboma poruszającymi się ładunkami.

W przewodniku z prądem każdy poruszający się elektron wytwarza wokół siebie układ „muszli” magnetycznych. Ponieważ te muszle przylegają ciasno do siebie, to w efekcie przewodnik z prądem jest otoczony cylindrycznym polem B. Powierzchnie o stałej wartości B tworzą układ już nie muszli, ale współosiowych cylindrów.

Kierunki prądu I oraz wektora B, jaki ten prąd wytwarza, są zgodne z regułą prawej dłoni: kciuk wskazuje kierunek prądu, a pozostałe palce pokazują jak pole B otacza przewodnik

Jeżeli przewodnik z prądem I podzielimy na nieskończenie krótkie odcinki o długości dl, to w każdym z nich będzie poruszał się ładunek dq i w odległości r pole magnetyczne tego odcinka prądu dB wyniesie

Otrzymane wyżej wyrażenie na pole magnetyczne dB odcinka z prądem I o długości dl

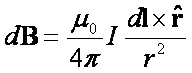
możemy scałkować po całej długości dowolnie zgiętego, a nawet splątanego, przewodnika.

Otrzymamy wtedy całkę krzywoliniową określającą pole B dawane przez cały ten przewodnik

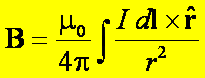
Ta całka wyraża prawo Biota i Savarta, które pozwala w zasadzie otrzymać pole B pochodzące od dowolnego przewodnika. Warunkiem jest, aby udało nam się przeprowadzić całkowanie po skomplikowanej krzywej. Metody numeryczne mogą okazać się tutaj niezastąpione.

Przykład zastosowania prawa Biota i Savarta.

Zadaniem jest znalezienie pola magnetycznego B na osi pętli kołowej o promieniu a w odległości x od jej środka gdy przez pętlę płynie prąd o natężeniu I. Pętlę prądową dzielimy na nieskończenie małe odcinki dl. Pole dB jednego takiego odcinka znajdujemy na podstawie prawa Biota i Savarta

Wektor dB dzielimy na dwie składowe: równoległą do osi x dB_x oraz prostopadłą do osi x dB_y. Składowe dB_y będą się kasowały przy obiegu pętli i tymi składowymi nie będziemy się dalej zajmowali. Dla sytuacji przedstawionej na rysunku

możemy napisać

Zatem

W środku pętli, gdy x maleje do zera (x = 0) pole B ma wartość

Dla ściśle nawiniętej cewki z N zwojami

Back to Index