Back to Index

PRĄD ELEKTRYCZNY.

OPORNOŚĆ R.

SIŁA ELEKTROMOTORYCZNA

* Prąd elektryczny

* Opór przewodnika

* Oporność

* Szeregowe, równoległe i mostkowe łączenie oporników

* Siła elektromotoryczna

* Prawa Kirchhoffa dla prądu stałego

* Praca i moc w obwodach elektrycznych prądu stałego

Zakończyliśmy już omawianie elektrostatyki i teraz ładunki puszczamy w ruch. Ruch ładunków jest źródłem niezwykle pasjonujących zjawisk, których opisem zajmiemy się przez wiele kolejnych wykładów. Podstawowym takim zjawiskiem jest prąd elektryczny.

.

Ładunki w ruchu tworzą prąd elektryczny. Ruch ładunku w przewodniku jest wynikiem nałożenia się ruchu przypadkowego i stałego dryfu. Ilościową miarą prądu jest wielkość nazwana natężeniem prądu I, która jest szybkością przenoszenia ładunku wypadkowego Q przez pewną powierzchnię. Zamiast terminu „natężenie prądu” będziemy zwykle używali krótszego terminu „prąd”. Przypominamy, że prędkością zmiany pewnej wielkości nazywamy stosunek (iloraz) wartości tej zmiany do czasu, w jakim ona nastąpiła. Najbardziej ścisłym określeniem prędkości jest pochodna po czasie funkcji opisującej analizowaną wartość. Dlatego prąd średni określamy zależnością

a prąd chwilowy jako

Jednostką natężenia prądu jest amper 1 A = 1 C/1 s, co oznacza prędkość przenoszenia ładunku jednego kulomba w czasie jednej sekundy.

Jeżeli średnia gęstość nośników prądu w przewodniku o przekroju A wynosi n, a średnia prędkość tych nośników jest v, to w czasie Δt zostanie przeniesiony ładunek ΔQ

Prąd płynący przez jednostkowy przekrój przewodnika nazywamy gęstością prądu j:

Zauważmy, że tutaj powierzchni i prędkości nadaliśmy cechy wektora.

Wektor gęstości prądu j ma zawsze ten sam kierunek, jak pole elektryczne E.

Jeżeli przyłożymy do przewodnika różnicę potencjałów (napięcie) V i to napięcie wywoła w przewodniku przepływ prądu I, to stosunek obu tych wielkości określa opór przewodnika R

Powyższe równanie jest znane jako prawo Ohma.

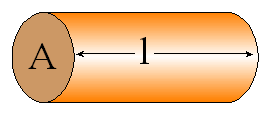
Opór przewodnika jest wprost proporcjonalny do jego długości l i odwrotnie proporcjonalny do przekroju poprzecznego A

Współczynnik ρ nazywamy opornością materiału przewodnika.

Oporność materiału określa zdolność tego materiału do tworzenia oporu stanowiącego przeszkodę w przepływie prądu. Oporność oznaczamy symbolem ρ i definiujemy ją jako

Przykładowe oporności materiałów (ρ, Om·m):

Przewodniki

srebro, miedź . 1.5 × 10^-8

złoto, aluminium . 2.5 × 10^-8

stal, ołów . 2 × 10^-7

Półprzewodniki

Ge 0.6

Si 2300

Izolatory

szkło 10¹⁰ - 10¹⁴

drewno 10⁸ - 10¹¹

kwarc (topiony) 7.5 × 10¹⁷

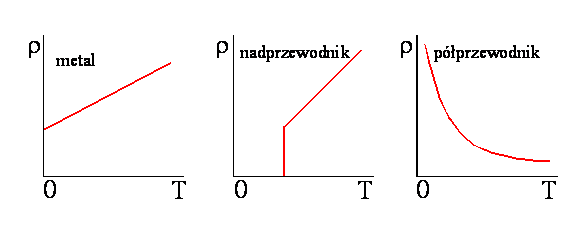
Zależność oporności od temperatury dla metali można wyrazić przez przybliżone równanie

gdzie ρ₀ jest wartością w temperaturze odniesienia T₀ zaś α jest temperaturowym współczynnikiem oporności.

Zależność oporności od temperatury dla półprzewodników jest opisywana przez równanie

gdzie stała C jest niezależna od temperatury

Łączenie szeregowe oporników. Spadek potencjału na układzie szeregowym jest równy sumie spadków na poszczególnych opornikach

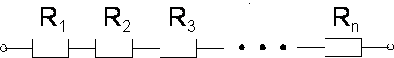
Stąd sumaryczny opór R układu szeregowego jest określony wzorem

Łączenie równoległe oporników. W połączeniu równoległym

spadek potencjału na każdym z oporników jest taki sam i prąd płynący przez układ rówoległy jest sumą prądów płynących przez poszczególne oporniki

Na podstawie prawa Ohma otrzymujemy stąd sumaryczny opór R układu równoległego

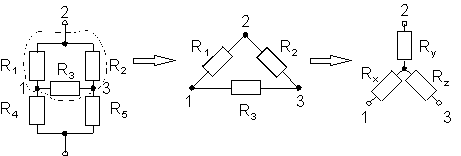
DLA DOCIEKLIWYCH

Łączenie mostkowe oporników. Aby obliczyć oporność zastępczą układu mostkowego oporników postępujemy analogicznie jak w przypadku połączenia mostkowego kondensatorów. Do oporników połączonych mostkowo również zastosujemy zamianę trójkąta oporników w równoważną gwiazdę.

Połączenia mostkowego nie możemy bezpośrednio zastąpić żadną kombinację połączeń szeregowych i równoległych.

Oporności między punktami 1-2, 2-3 i 3-1, które oznaczamy jako R₁₂, R₂₃ i R₃₁, powinny być takie same w trójkącie jak i w równoważnej mu gwieździe. Na podstawie wartości oporności R₁, R₂ i R₃ należy obliczyć R_x, R_y i R_z. Warunki równości oporności w obu konfiguracjach, dla trójkąta i dla gwiazdy, zapisujemy jako

Stąd otrzymujemy poszukiwane wartości R_x, R_y i R_z:

;

Po zamianie trójkąta w gwiazdę znika już połączenie mostkowe a w jego miejsce otrzymujemy prostą i łatwą do obliczenia kombinację połączeń szeregowych i równoległych oporników

Siła elektromotoryczna

Siłą elektromotoryczną nazywamy różnicę potencjałów, która powoduje przepływ prądu w całym obwodzie włączając w to także prąd, jaki płynie przez samo źródło zasilania (np. baterię). Dla idealnego źródła, czyli takiego, które ma zerowy opór wewnętrzny r, siła elektromotoryczna jest równa napięciu dawanemu przez to źródło, gdy jest ono podłączone do opornika zewnętrznego R

Każde źródło rzeczywiste ma zawsze pewien opór wewnętrzny r i dlatego napięcie dawane przez to źródło V_ab jest zawsze mniejsze od siły elektromotorycznej źródła

Wprowadzimy pojęcie węzła w sieci elektrycznej oraz oczka w obwodzie elektrycznym. Węzłem nazywamy taki punkt w obwodzie elektrycznym, w którym łączą się więcej niż dwie gałęzie (przewody). Oczkiem (pętlą) nazywamy dowolny zamknięty fragment obwodu elektrycznego. Pętla może być prostym połączeniem nie zawierającym żadnych rozgałęzień, ale też może być w dowolny sposób rozgałęziona. Musi tylko być zamknięta w tym sensie, że przy obchodzeniu pętli punkt końcowy drogi musi pokrywać się z punktem początkowym.

Prawa Kirchhoffa orzekają:

1. Dla węzła: Suma algebraiczna prądów wpływających do węzła i z niego wypływających jest równa zeru.

2. Dla oczka (pętli): Suma algebraiczna różnic potencjałów wzdłuż zamkniętego obwodu, łącznie z siłami elektromotorycznymi źródeł i spadkami IR, musi równać się zeru.

Spróbuj swoich sił i odpowiedz ile oczek widzisz w obwodzie ze schematu poniżej? Jest ich o wiele więcej niż trzy!

Dla złożonych obwodów, w skład których mogą oprócz oporników wchodzić także kondensatory i cewki (obwodów RLC), analiza za pomocą drugiego prawa Kirchhoffa prowadzi do dużej liczby równań liniowych. Dla takiej dużej liczby równań mało użyteczne stają się wzory Cramera, które są użyteczne w przypadku dwóch lub trzech równań. Do rozwiązania układów dużej liczby równań liniowych niezwykle skuteczne są metody eliminacji Gaussa.

Na podstawie definicji potencjału elektrycznego wiemy, że iloczyn wartości potencjału i ładunku w nim umieszczonego określa energię tego układu. Ta energia jest równoważna pracy, jaka może zostać wykonana. Praca wykonywana przez prąd jest określona przez równanie

Moc prądu stałego, podobnie jak w mechanice, jest równa prędkości wykonywania pracy

Jednostką mocy jest1 wat; 1 W = 1V·1A

Back to Index