Back to Index

DIELEKTRYKI I ICH ROLA W KONDENSATORZE

WEKTORY E, D i P

POLE ELEKTRYCZNE W DIELEKTRYKU

UOGÓLNIONE PRAWO GAUSSA

* Dielektryki

* Rola dielektryka w kondensatorze

* Wektory E, D i P

* Pole elektryczne w dielektryku

* Gęstość energii pola elektrycznego w dielektryku

* Uogólnione prawo Gaussa

Dielektrykiem nazywamy ciało gazowe, ciekłe lub stałe niebędące przewodnikiem prądu elektrycznego. Oznacza to, że ładunki elektryczne wchodzące w skład każdego ciała są w dielektryku związane ze sobą w tym znaczeniu, że mogą być przesuwane tylko w obrębie dielektryka. Jeżeli do dielektryka przyłożymy pole elektryczne to przesunięcie ładunków pod działaniem tego pola spowoduje polaryzację dielektryka, czyli nadanie jego warstwie niezerowego momentu dipolowego. Oznacza to, że między okładkami naładowanego kondensatora powierzchnia dielektryka sąsiadująca z okładką naładowaną dodatnio uzyska pewien ładunek ujemny. I odwrotnie, okładka naładowana ujemnie będzie sąsiadowała z dodatnio naładowaną powierzchnią dielektryka. Najważniejszym skutkiem polaryzacji dielektryka jest to, że część ładunku na okładkach kondensatora jest zneutralizowana i już nie bierze udziału w wytwarzaniu pola elektrycznego między okładkami.

Częściowa, ale nie całkowita, neutralizacja (kompensacja) ładunku elektrod przez warstwę dielektryka jest związana z faktem, ze polaryzacja dielektryka jest spowodowana przez orientację dipoli istniejących wewnątrz dielektryka. Takie dipole można z grubsza podzielić na dipole trwałe i dipole indukowane. Dipole trwałe występują w substancjach, których molekuły mają trwały moment dipolowy. Tutaj wyrazistym przykładem jest woda, która ulega w polu elektrycznym bardzo silnej polaryzacji. Dipole indukowane nie występują wtedy, kiedy nie ma przyłożonego pola elektrycznego a pojawiają się w atomie lub molekule dopiero pod działaniem tego pola. Pole zewnętrzne deformuje ładunek elektronowy atomów i molekuł powodując, że środek ładunku ujemnego elektronów nie pokrywa się już ze środkiem ładunku dodatniego jąder i w ten sposób pojawia się moment dipolowy, który natychmiast znika po wyłączeniu pola. Przykładem może być benzen C₆H₆ nie mający żadnego trwałego momentu dipolowego a uzyskujący ten moment dopiero pod działaniem pola. Oczywiście, również substancje złożone z molekuł mających trwałe momenty dipolowe ulegają słabej dodatkowej polaryzacji indukowanej. Polaryzacja kryształów jonowych polega na tym, że dodatnie i ujemne jony zostają przesunięte względem siebie pod wpływem przyłożonego pola, a w niektórych substancjach pewną rolę może także odgrywać polaryzacja ruchomego ładunku przestrzennego (np. domieszek jonowych).

Orientacja dipoli w dielektryku nie jest nigdy idealna i dlatego nie mamy całkowitej kompensacji ładunku elektrod kondensatora wypełnionego dielektrykiem. Powodem braku całkowitej orientacji dipoli są głównie dezorganizujące ruchy termiczne, ale też ograniczenia narzucone przez strukturę krystaliczną warstwy dielektryka i przeszkody w obrotach molekuł ze strony innych molekuł. Pełnej orientacji dipoli, czyli całkowitej polaryzacji dielektryka nie osiągamy, zatem, aż do napięcia przebicia dielektryka.

Co się stanie z pojemnością kondensatora, jeżeli przestrzeń między jego okładkami wypełnimy dielektrykiem? Wydarzy się wtedy bardzo wiele!

Okazuje się, że pojemność kondensatora wypełnionego dielektrykiem jest wielokrotnie większa od pojemności kondensatora pustego (wypełnionego powietrzem). Zobaczmy, co jest powodem tego bardzo ważnego zjawiska. Pojemność kondensatora C naładowanego ładunkiem Q przy różnicy potencjałów między okładkami wynosi na podstawie definicji

Chociaż całe poniżej przedstawione rozumowanie jest słuszne dla każdego rodzaju kondensatora to ograniczymy się dalej do najprostszego przypadku kondensatora płaskiego.

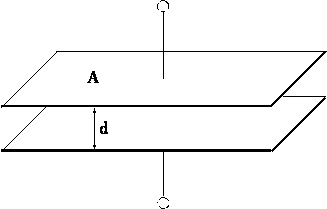
Poprzednio otrzymaliśmy, stosując prawo Gaussa, wzór na pojemność takiego kondensatora

Jeżeli ten przykładowy kondensator płaski naładujemy stałym ładunkiem Q symbolizowanym na lewym rysunku poniżej dwoma znakami plus i dwoma minus (ładunki na okładkach powstają przez przesunięcie ładunku i muszą być jednakowe co do wartości) to natężenie pola E będzie symbolizowane przez dwa wektory mające początek na ładunku plus a koniec na ładunku minus. Liczba ładunków na okładkach przedstawionych na rysunku jest tylko symboliczna – w rzeczywistości ta liczba jest liczona w wielu miliardach.

Napięcie między okładkami, odległymi od siebie o d, jest dane przez znany nam już wzór („napięcie krokowe”)

Jeżeli teraz między okładki wstawimy dipol, tak jak na prawym rysunku powyżej, to jeden z wektorów E zostanie usunięty z przestrzeni miedzy elektrodami przez przeciwnie skierowane pole dipola. Pole E zostało zmniejszone o połowę a zatem również o połowę zmniejszy się napięcie między okładkami . Ponieważ kondensator jest odłączony od źródła zasilania to ładunek na elektrodach nie może ulec zmianie i kiedy zastosujemy wzór definiujący pojemność

to stwierdzamy, że pojemność kondensatora stała się dwa razy większa. Jeżeli oznaczymy pojemność kondensatora lewego jako C_lewy, a prawego jako C_prawy to widzimy od razu, że

oraz

czyli, że w tym symbolicznym przypadku pojemność kondensatora z dielektrykiem wzrosła dwukrotnie

W rzeczywistości działanie dielektryka jest dużo bardziej efektywne i zwiększenie pojemności kondensatora wypełnionego dielektrykiem może wynieść kilkanaście, kilkadziesiąt, a nawet kilkaset razy.

Zupełnie analogicznie otrzymujemy zwiększenie pojemności kondensatora po wypełnieniu go dielektrykiem wtedy, kiedy kondensator jest podłączony do źródła stałego napięcia V. Sytuację w kondensatorze „powietrznym” przedstawia rysunek poniżej

Na tym symbolicznym rysunku każdy ładunek plus daje początek wektorowi pola E, który kończy się na ładunku minus. Jeżeli teraz między okładki wstawimy dipol, jak na rysunku poniżej, to również i teraz jeden z wektorów E zostanie usunięty z przestrzeni miedzy elektrodami przez przeciwnie skierowane pole dipola.

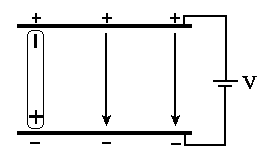
Powstała sytuacja, która jest niemożliwa do utrzymania. Przy podłączonym źródle stałego napięcia V natężenie pola E musi przecież być takie, aby była spełniona zależność . Aby tak się stało, ze źródła napięcia musi przepłynąć dodatkowy ładunek, który zastąpi ładunek skompensowany przez obecność dielektryka. Wtedy znowu mamy trzy wektory E, jak na rysunku poniżej, czyli tyle ile potrzeba aby zaspokoić wymaganie wyrażone we wzorze .

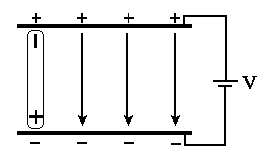
Teraz, przy niezmienionym napięciu, na kondensatorze jest większy ładunek, co oznacza, że pojemność kondensatora odpowiednio wzrosła. Aby scharakteryzować ilościowo wpływ dielektryka na pojemność kondensatora wprowadzamy dla tego dielektryka stałą materiałową, którą nazywamy względną przenikalnością elektryczną ε i którą definiujemy jako stosunek pojemności kondensatora wypełnionego dielektrykiem C do pojemności kondensatora pustego C₀

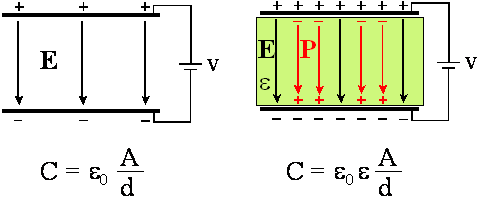
Dokładniejszy opis formalny zachowania się dielektryka w kondensatorze otrzymamy przez wprowadzenie dwóch dodatkowych wektorów: wektora polaryzacji P i wektora przesunięcia D. Wektor P pojawił się już awansem w rysunku powyżej. Zwróćmy szczególną uwagę na wektor D, którego długość jest równa gęstości całkowitego ładunku σ zgromadzonego na okładkach kondensatora i który wchodzi w równania Maxwella zapisywane w zwartej, eleganckiej postaci. Gdy pusty kondensator jest utrzymywany pod stałym napięciem V i gęstość ładunku na okładkach tego kondensatora oznaczymy przez σ₀, wtedy pole E miedzy okładkami jest takie, że

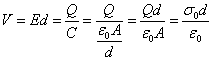, czyli

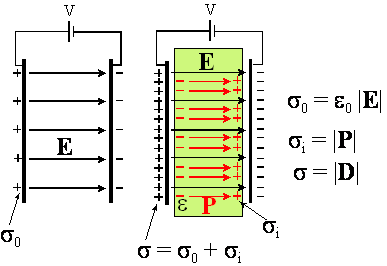
Teraz zadziała mechanizm polaryzacji dielektryka. Po wstawieniu dielektryka między okładki kondensatora, pole elektryczne między okładkami powoduje polaryzację dielektryka, co oznacza przesunięcie w kierunku okładek ładunków o przeciwnych znakach. Część ładunków na okładkach mająca gęstość σ₀ zostanie „zamaskowana” przez przeciwny ładunek indukcyjny o gęstości σ_i. Wtedy źródło napięcia musi doładować kondensator do takiej gęstości ładunku σ aby znowu natężenie pola między okładkami spełniało warunek V = Ed. Zatem σ = σ₀ + σ_i , czyli gęstość całkowitego ładunku na okładkach kondensatora z dielektrykiem jest równy sumie gęstości ładunku na kondensatorze bez dielektryka i gęstości ładunku polaryzacyjnego.

Jeżeli oznaczymy

σ₀ = ε₀ E,

σ_i = P

σ = D

i zastosujemy prawo Gaussa do kondensatora z dielektrykiem wtedy natychmiast otrzymujemy związek

czyli

Ten związek między wektorami D, E i P zapisuje się w postaci wektorowej

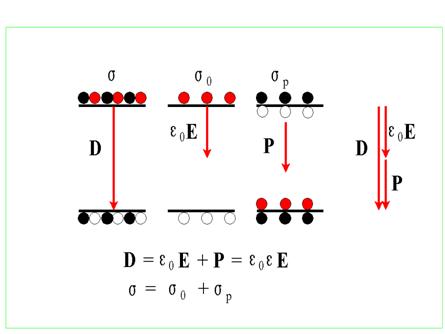
Przypominamy, że D jest wektorem przesunięcia („displacement”), E wektorem pola i P wektorem polaryzacji. Wektor P (na rysunku poniżej oznaczony na czerwono) działa wewnątrz dielektryka i rysujemy go jako strzałkę od „minusa” do „plusa”, czyli odwrotnie niż wektor E.

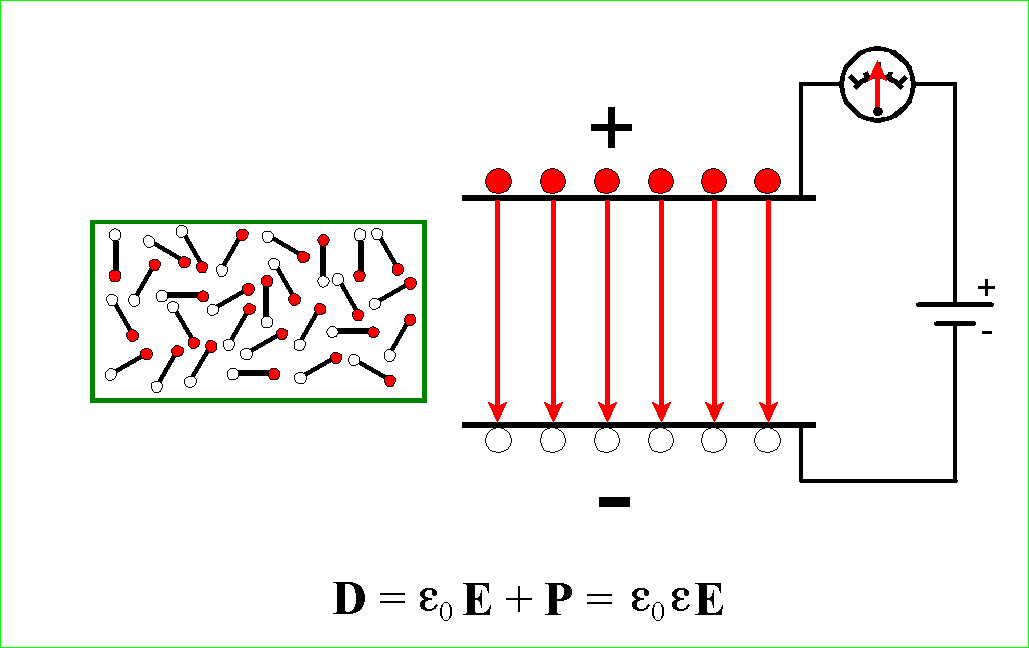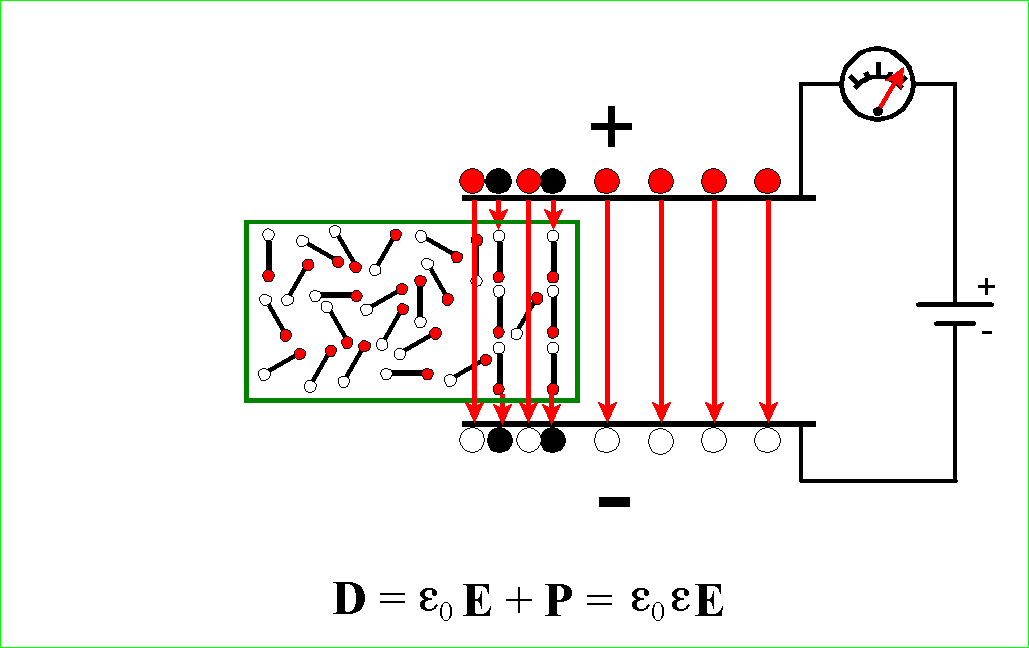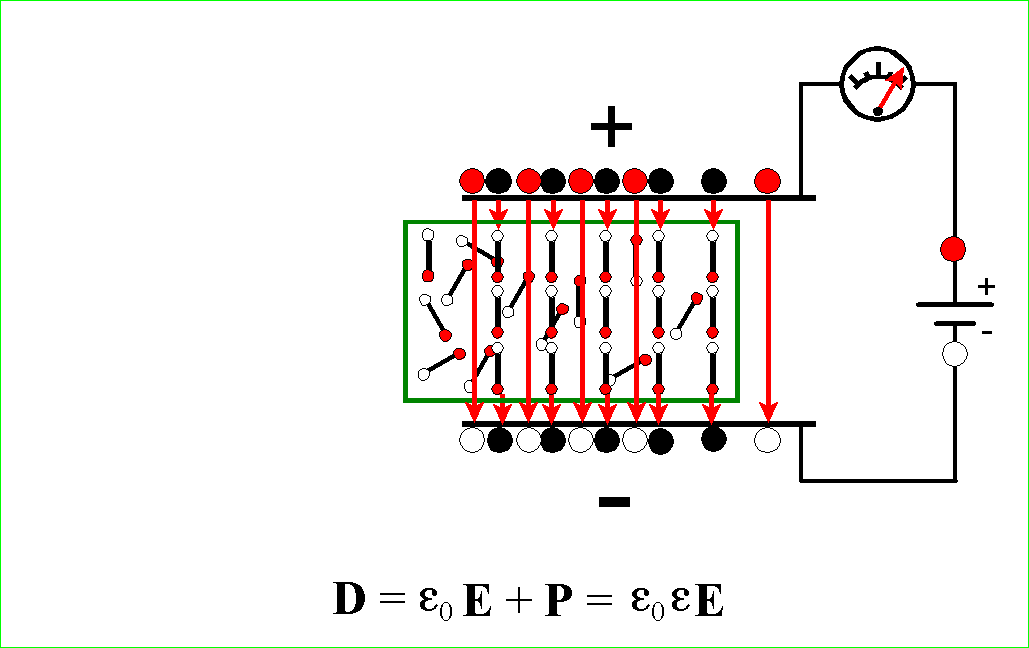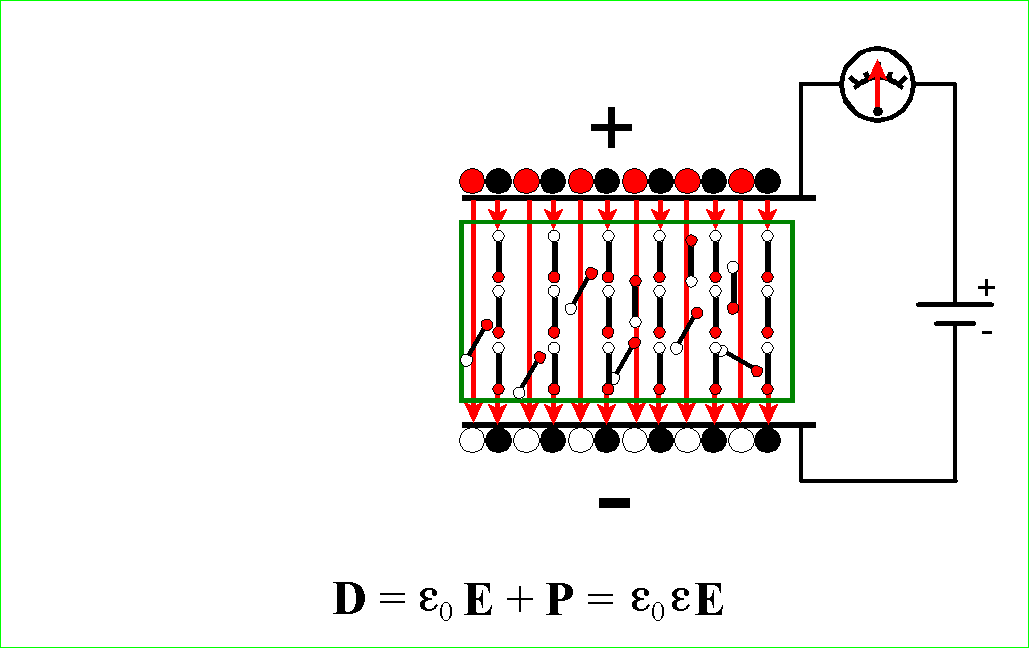
Jak już mówiliśmy, względna przenikalność elektryczna materiału (stała dielektryczna) jest oznaczana przez ε i definiowana jako stosunek pojemności kondensatora wypełnionego dielektrykiem C do pojemności kondensatora pustego C₀.

Pamiętajmy, że kondensator jest stale podłączony do źródła napięcia, czyli V = Q/C = const. Pojemność kondensatora z dielektrykiem wyniesie

a pojemność pustego kondensatora będzie

Na tej podstawie możemy napisać

Stąd

Po podstawieniu do wyrażenia otrzymujemy równoważne określenie wektora D:

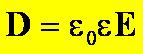
Jeżeli kondensator NIE jest podłączony do źródła zasilania to ładunek Q = CV na jego okładkach pozostanie stały niezależnie od tego czy między nimi będzie umieszczony dielektryk czy też nie. Jeżeli oznaczymy przez C₀ i E₀ odpowiednio pojemność pustego kondensatora i wartość pola elektrycznego między jego okładkami a przez C i E analogiczne wielkości dla kondensatora wypełnionego dielektrykiem to możemy napisać

Stąd i na podstawie definicji przenikalności elektrycznej ε otrzymujemy

Widać, zatem, że natężenie pola w dielektryku jest mniejsze ε razy niż w próżni

Ta relacja jest ogólna i obowiązuje w każdym stałym polu E, niezależnie od źródła jego pochodzenia.

Prawo Coulomba w dielektrykach. Obniżenie ε-krotne natężenia pola w dielektrykach ma ogromne znaczenie praktyczne. Jednym z głównych jest ε-krotne zmniejszenie się siły Coulomba gdy oddziałujące ładunki są zanurzone w dielektryku:

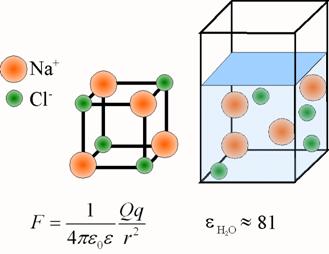
Dzięki temu efektowi możliwe jest rozpuszczanie substancji o wiązaniu jonowym w rozpuszczalnikach o dużej przenikalności ε. W szczególności możliwe jest solenie potraw, ponieważ w wodzie o ogromnej wartości ε = 81 kryształ NaCl złożony z kationów Na⁺ i anionów Cl^-, utrzymywany siłami Coulomba, „rozsypuje się” przechodząc do roztworu elektrolitu.

Gęstość energii pola elektrycznego E w dielektryku jest ε razy większa niż w próżni i wynosi

Wykorzystując zależność wyrażenie na gęstość energii możemy zapisać w zwartej postaci wektorowej

To wyrażenie obowiązuje zawsze, także dla przypadku kryształów gdzie wektory E i D nie są na ogół równoległe do siebie.

1. Wkładanie i wyjmowanie dielektryka z okładek kondensatora o stałym ładunku sumarycznym, jak na rysunku, powoduje przelewanie się ładunku z jednego kondensatora do drugiego. Żarówka może świecić.

2. Gęstość ładunku na okładce kondensatora częściowo wypełnionego dielektrykiem nie jest stała. A co jest stałe na powierzchniach okładek?

Opisując siłę Coulomba między ładunkami punktowymi znajdującymi się w dielektryku przenikalność elektryczną próżni pomnożyliśmy przez przenikalność dielektryka i zamiast ε₀ użyliśmy iloczynu ε₀ε. To postępowanie możemy uogólnić i zastosować je również do prawa Gaussa, gdy ośrodkiem, przez który przenika pole jest nie próżnia, ale dielektryk. Wtedy znane nam prawo Gaussa

będziemy mogli napisać w postaci

czyli

Jeżeli wykorzystamy teraz relację

to otrzymamy ostateczną postać uogólnionego prawa Gaussa

Prawo Gaussa w tej postaci obowiązuje tak w próżni, gdzie ε = 1, jak i w dielektrykach. Ładunek Q w tym równaniu jest, jak i poprzednio, wypadkowym ładunkiem zawartym wewnątrz powierzchni zamkniętej, po której przeprowadza się całkowanie.

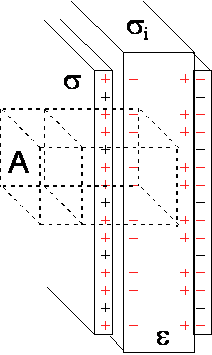
W kondensatorze z dielektrykiem ładunkiem wypadkowym jest różnica między ładunkiem zgromadzonym na okładce q₁ = σA i ładunkiem polaryzacyjnym (o przeciwnym znaku) indukowanym w warstwie powierzchniowej dielektryka q₂ = - σ_iA. Jeżeli do takiej struktury zastosujemy prawo Gaussa to przyjmiemy, że ładunki są zgromadzone na sąsiadujących powierzchniach okładki i dielektryka i że pole nie wychodzi poza okładki kondensatora. Naturalnym wyborem powierzchni Gaussa, po której będziemy przeprowadzali całkowanie strumienia, jest prostopadłościan (lub powierzchnia walca itp.). Podstawa prostopadłościanu o powierzchni A jest równoległa do powierzchni okładki. Jedna podstawa znajduje się poza okładką (gdzie nie ma pola) a druga jest umieszczona wewnątrz dielektryka

Prawo Gaussa w przedstawionej wyżej postaci jest jednym z czterech równań Maxwella opisujących wszystkie zjawiska elektryczne, magnetyczne i optyczne. Równania Maxwella są fundamentalnymi prawami elektrodynamiki i żadnego z nich nie można wyprowadzić z praw jeszcze prostszych – można je tylko próbować uzasadnić. Gdyby istniały prawa jeszcze bardziej podstawowe, to z całą pewnością zostałyby one tutaj przedstawione. Równania te są wynikiem twórczego natchnienia, olśnienia ich twórców Gaussa, Faradaya i Ampere’a. Maxwell wprowadził do nich genialną koncepcję „prądu przesunięcia”, o którym opowiemy nieco później, co pozwoliło ujednolicić strukturę tych równań i rozszerzyć je na przypadek fal elektromagnetycznych a zatem również i fal świetlnych.

Back to Index