Back to Index

POTENCJAŁ POLA ELEKTRYCZNEGO

LINIE SIŁ POLA ELEKTRYCZNEGO I POWIERZCHNIE EKWIPOTENCJALNE

GRADIENT POTENCJAŁU A POLE E

* Energia potencjalna U ładunku w polu E i potencjał V pola E

* Linie sił pola elektrycznego i powierzchnie ekwipotencjalne

* Gradient potencjału a pole E

Podejście energetyczne jest bardzo skuteczne w opisie zjawisk elektrycznych ponieważ możliwe jest zdefiniowanie energii potencjalnej U ładunku w polu elektrycznym. Rozważmy pole elektryczne między dwiema równoległymi płytami, na których znajdują się ładunki o jednakowej wartości, ale o przeciwnych znakach. Rozmiary płyt są duże w porównaniu z odległością między nimi, a zatem na przeważającym obszarze pole między nimi może być traktowane jako jednorodne. Mały dodatni ładunek punktowy +q ma największą energię potencjalną U wtedy, gdy znajduje się w punkcie na powierzchni elektrody dodatniej, jak na rysunku.

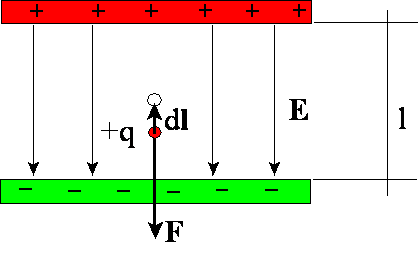
Oznacza to, że w tym punkcie ładunek +q ma najwyższą zdolność do wykonania pracy w czasie swojego powrotu do elektrody ujemnej. Tę energię potencjalną U musimy ładunkowi nadać wykonując pracę W przeniesienia tego ładunku od elektrody ujemnej do dodatniej. Pracę wykonujemy pokonując siłę odpychania elektrostatycznego F = qE. Na odcinku dl wykonamy pracę dW równą

czyli

Praca przeniesienia ładunku +q między obiema elektrodami, czyli energia potencjalna U tego ładunku na dodatniej elektrodzie, wynosi

Ponieważ pole elektryczne jest polem potencjalnym, to praca przeniesienia ładunku z punktu a do punktu b nie zależy od kształtu drogi ładunku między tymi punktami

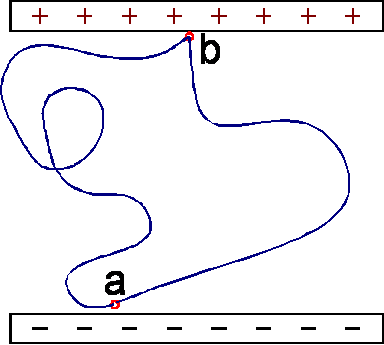
Poprzednio zdefiniowaliśmy natężenie pola elektrycznego jako siłę działającą na ładunek jednostkowy. W podobny sposób definiujemy potencjał elektryczny V albo po prostu potencjał, jako stosunek energii potencjalnej, jaką ma w polu elektrycznym ładunek q, do wartości tego ładunku. Jeżeli, zatem, dowolny ładunek q ma w jakimś punkcie pola energię potencjalną U, to potencjał pola V w tym punkcie wynosi

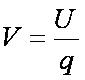
W ogólnym przypadku kiedy pole E nie jest jednorodne powinniśmy napisać związek ogólny, który jest zresztą słuszny i dla pola jednorodnego

Teraz natężenie pola E możemy wyrazić poprzez spadek potencjału dV na odcinku dl:

Kiedy kierunek przesunięcia dl nie jest równoległy do kierunku pola E, wtedy ogólny związek między dyskutowanymi wielkościami otrzymamy zapisując go w postaci wektorowej. Spadek potencjału dV będzie wtedy iloczynem skalarnym i w ogólnym przypadku pola niejednorodnego przyrosty dU i dV wynoszą

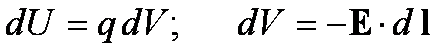
Różnicę potencjałów V_ab między punktami a i b na rysunku powyżej, nawet gdyby pole było niejednorodne, otrzymamy przez całkowanie

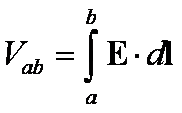
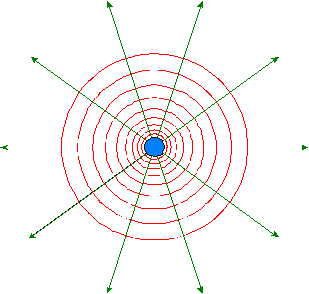
Liniami pola E nazywamy tory próbnych ładunków dodatnich poruszających się pod działaniem tego pola. Powierzchnie, na których potencjał elektryczny ma jednakową wartość nazywamy powierzchniami ekwipotencjalnymi. Linie pola E (zielone) są zawsze prostopadłe do powierzchni ekwipotencjalnych (czerwone). Rysunek poniżej przedstawia otoczenie ładunku punktowego

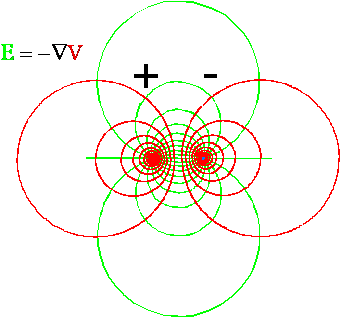
Rozkład linii pola E (zielone) prostopadłych do powierzchni ekwipotencjalnych (czerwone) w otoczeniu dipola można przedstawić następująco

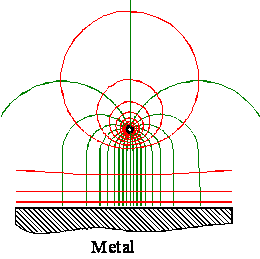
Powierzchnia metalu jest zawsze powierzchnią ekwipotencjalną (zastanów się, dlaczego?). Zatem kiedy ładunki będące w spoczynku są rozmieszczone na powierzchni metalu, to pole elektryczne bezpośrednio nad powierzchnią tego metalu musi być prostopadłe do jego powierzchni w każdym jej punkcie.

Ponieważ, jak to pokazaliśmy wyżej, natężenie pola E jest związane ze spadkiem potencjału dV i odległością dl, na której ten spadek zachodzi za pomocą wzoru

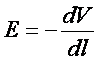
to wektor natężenia pola E można określić bezpośrednio jako spadek (gradient) potencjału

Otrzymana relacja między wektorem pola E i gradientem potencjału

jest to bardzo użyteczna z powodów praktycznych ponieważ wystarczy w pewnym punkcie znaleźć potencjał pola V wyrażony jako funkcja współrzędnych (wielkość skalarną), aby niemal automatycznie otrzymać trudniejszą do obliczenia wielkość wektorową E. Jak pamiętamy z własności funkcji wektorowych, gradient funkcji skalarnej (w tym przypadku potencjału V) jest wielkością wektorową E. Składowe tego wektora są wyrażone przez pochodne cząstkowe (spadki wzdłuż x, y i z)

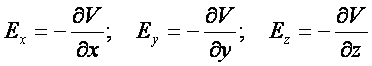
Jeżeli pole E jest stałe i jednorodne to wtedy gradient potencjału jest również stały i teraz bardzo prostą i wygodną regułą określania różnicy potencjału V (napięcia) w tym polu jest relacja, która wynika bezpośrednio ze związku między E i gradientem potencjału

gdzie odległość l jest liczona wzdłuż pola. Regule tej podlega zmiana napięcia pokazywanego przez woltomierz jeżeli będziemy płynnie zmieniali położenie jego końcówek stykających się z drutem oporowym przez który płynie prąd. Napięcie określone według tej reguły nosi nazwę napięcia krokowego. Nazwa „napięcie krokowe” powstała z zagrożenia porażeniem elektrycznym wtedy, gdy stawiamy długie kroki (np. biegniemy) a niedaleko od nas piorun uderzy w ziemię. Napięcie krokowe jest groźne dla bydła pozostającego na łące w czasie burzy.

W eksperymencie można zmierzyć jedynie różnicę potencjałów. Jednostką potencjału elektrycznego i różnicy potencjałów jest 1 wolt ( 1V = 1J/1C).

Back to Index