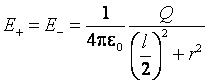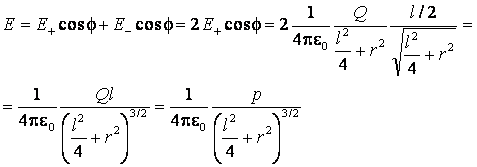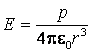Back to Index

PRAWO COULOMBA

POLE ELEKTRYCZNE E. DIPOL ELEKTRYCZNY

*Wstęp

* Ładunki elektryczne i elektryzacja ciał

* Prawo Coulomba

* Definicja pola elektrycznego

* Dipol elektryczny

W drugim semestrze wiodącym tematem będzie ELEKTRODYNAMIKA wraz z OPTYKĄ FALOWĄ, która może być traktowana jako uwieńczenie elektrodynamiki.

ZWIERZĘTAMI POCIĄGOWYMI BĘDĄ DLA NAS W TYM SEMESTRZE DWIE DZIKIE BESTIE, KTÓRE W POPRZEDNIM SEMESTRZE SIEDZIAŁY JESZCZE W KLATCE

SĄ TO (patrz temat 19.)

DYWERGENCJA (MAMA) oraz ROTACJA (TATA)

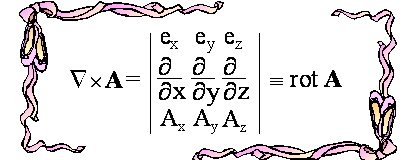
TEN MAŁY (JESZCZE ROŚNIE) POŚRODKU TO GRADIENT, który dzielnie się spisywał przy opisie zjawisk transportu w temacie 28.

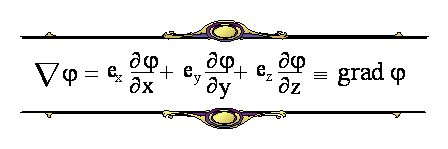
SZYBKO SIĘ PRZEKONAMY, ŻE SĄ TO NIEZWYKLE ŁAGODNE I POŻYTECZNE STWORZONKA:

DAJĄ SIĘ BARDZO ŁATWO OSWOIĆ

Te wspaniałe zalety charakteru mają jednak tylko

gradient, dywergencja i rotacja.

PAMIĘTAJ

CAŁĄ ELEKTRYCZNOŚCIĄ I MAGNETYZMEM, ŁĄCZNIE Z OPTYKĄ, RZĄDZĄ CZTERY RÓWNANIA MAXWELLA

w postaci całkowej

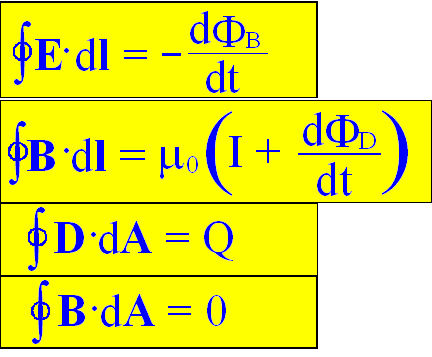
oraz w postaci różniczkowej

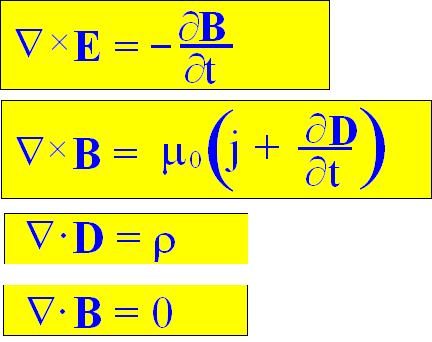
JAK WIDAĆ, RÓWNANIA MAXWELLA SĄ WYRAŻONE W JĘZYKU RACHUNKU WEKTOROWEGO, ŁACZNIE Z DYWERGENCJĄ I ROTACJĄ

DRUGI SEMESTR ZAKOŃCZYMY ELEMENTARNYM OPISEM BUDOWY JĄDRA ATOMOWEGO I POWŁOKI ELEKTRONOWEJ ATOMU

Ładunki elektryczne, dodatnie i ujemne, są skwantowane, czyli że mają pewną najmniejszą wartość, której nie można już dalej podzielić. Nie można ładunków stworzyć, ani zniszczyć w tym sensie, że sumaryczny ładunek w dowolnym procesie pozostaje stały. Gdy atom nie jest zjonizowany, to jego sumaryczny ładunek wynosi zero. Atomy zjonizowane z nadwyżką ładunku ujemnego nazywamy anionami, a z niedoborem ładunku ujemnego (z nadwyżką ładunku dodatniego) nazywamy kationami.

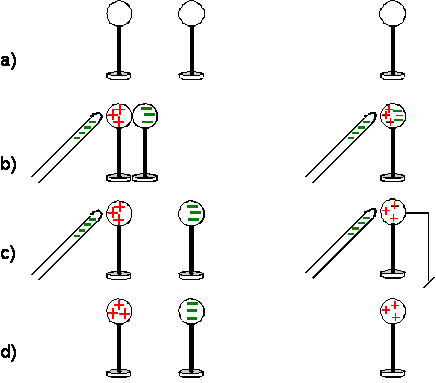
Elektryzacja ciał polega na przenoszeniu ładunku z jednego z nich do drugiego. W najprostszy sposób ciała mogą zostać naelektryzowane przez ich wzajemne pocieranie, co jest związane z przebudową elektrycznej warstwy podwójnej znajdującej się na powierzchni każdego z tych ciał. Innym sposobem elektryzacji, jest elektryzowanie przez indukcję jak to pokazane na rysunkach poniżej. Tutaj elektryzacji podlegają metalowe kule (białe) osadzone na izolatorze (czarny pręt). Rozseparowanie ładunków następuje przez zbliżenie ujemnie naładowanej laski izolatora naelektryzowanego przez tarcie o tkaninę.

W układzie SI jednostką ładunku jest 1 kulomb (1 C). Ładunek statyczny, zgromadzony np. na grzebieniu przez pocieranie, jest rzędu 10^-6 C (mikrokulomb, ok. 10¹³ elektronów). Ładunek elektronu wynosi 1.602×10^-19 C.

Prawo Coulomba (1736 - 1806) - prawo opisujące siłę oddziaływania między punktowymi ładunkami elektrycznymi Q i q znajdującymi się w odległości R i pozostającymi w spoczynku względem siebie.

Siłę oddziaływania między takimi ładunkami, czyli siłę Coulomba, opisuje wzór

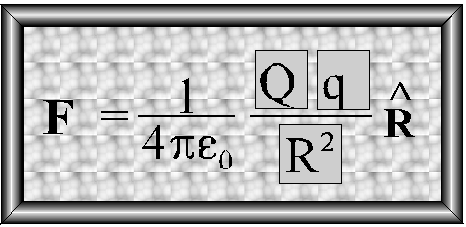
W układzie SI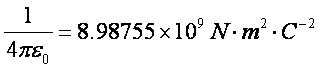

Wzór Coulomba automatycznie wyraża fakt, że ładunki jednoimienne odpychają się, a różnoimienne przyciągają się do siebie.

Aby potwierdzić swoje prawo eksperymentalnie, Coulomb dzielił ładunek zgromadzony na kuli przewodzącej przez przenoszenie jego połowy na taką samą kulę. Otrzymał 1/2, 1/4, ... ładunku pierwotnego. Stosując do pomiaru sił oddziaływania między ładunkami wagę skręceń

Coulomb pokazał, że dla ładunków punktowych siła oddziaływania wynosi rzeczywiście

W późniejszych bardzo dokładnych eksperymentach pokazano, że kwadrat w mianowniku jest 2 z dokładnością 2 ± 2×10^-16. Kierunek siły Coulomba pokrywa się z kierunkiem prostej łączącej oba ładunki punktowe. Równanie Coulomba stosuje się jedynie do przypadku ładunków punktowych. Gdy rozkład ładunków jest przestrzenny, wtedy należy przeprowadzić odpowiednie sumowanie lub całkowanie. Poza tym, że prawo Coulomba dotyczy tylko ładunków punktowych, to opisuje siłę działającą między nimi tylko wtedy, gdy ładunki znajdują się w spoczynku względem siebie. Na ładunki w ruchu działają dodatkowe siły, o czym będzie mowa w dalszej części kursu.

Pole elektryczne (natężenie pola) E w określonym punkcie definiujemy jako wielkość równą stosunkowi siły F działającej na dodatni ładunek próbny q do wartości tego ładunku:

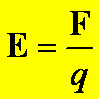
Zgodnie z definicją natężenia pola E, ruch cząstek naładowanych w tym polu odbywa się pod działaniem siły F = qE.

Addytywność pól.

Pole E jest addytywne wektorowo co oznacza, że wypadkowe pole elektryczne jest sumą wektorową pól E₁, E₂, E₃ ... pochodzących od indywidualnych ładunków :

Linie sił pola elektrycznego

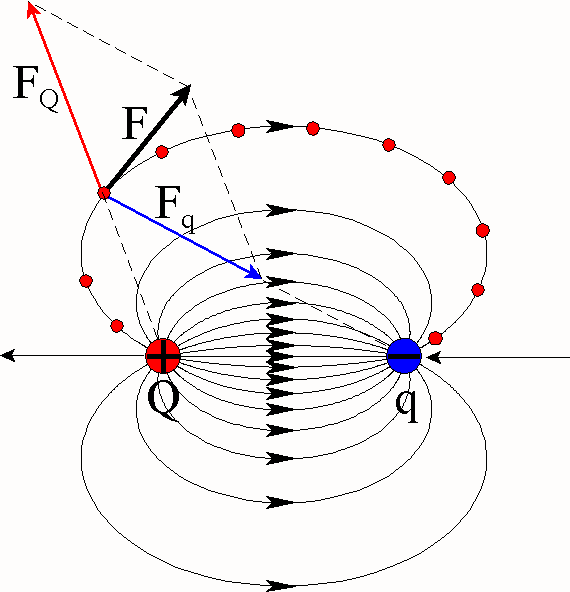
Koncepcja linii sił pola została wprowadzona również przez Michaela Faraday’a (1791-1867). Linie sił pola są to wyimaginowane krzywe w przestrzeni, będące w każdym punkcie styczne do wektora E w tym punkcie. Oznacza to również, że w każdym punkcie linii pola istnieje styczny wektor siły działającej w tym polu na ładunek próbny (mały ładunek dodatni). Jak pokazano na rysunku poniżej, linia sił jest zatem trajektorią dodatniego ładunku próbnego (mała czerwona kulka) poruszającego się w polu E, przy czym siła F jest wypadkową (sumą wektorową) dwóch sił: siły odpychającej ładunek próbny od ładunku dodatniego F_Q oraz siły przyciągającej ładunek próbny do ładunku ujemnego F_q. Taki obraz linii sił jest prawdziwy tylko przy zaniedbaniu sił bezwładności (odśrodkowych) wynikających z niezerowej masy ładunku. Linie sił pola nigdy nie przecinają się ze sobą. 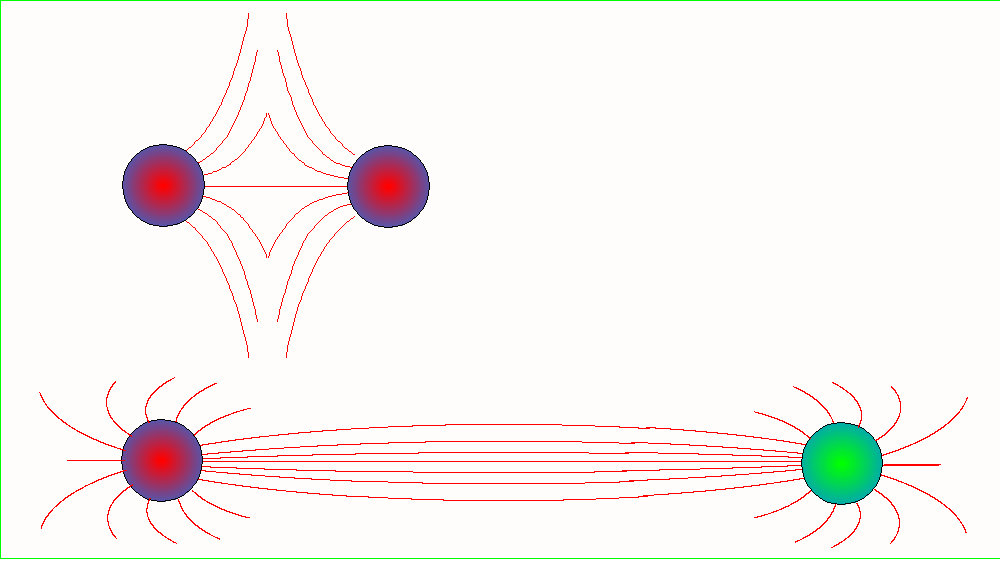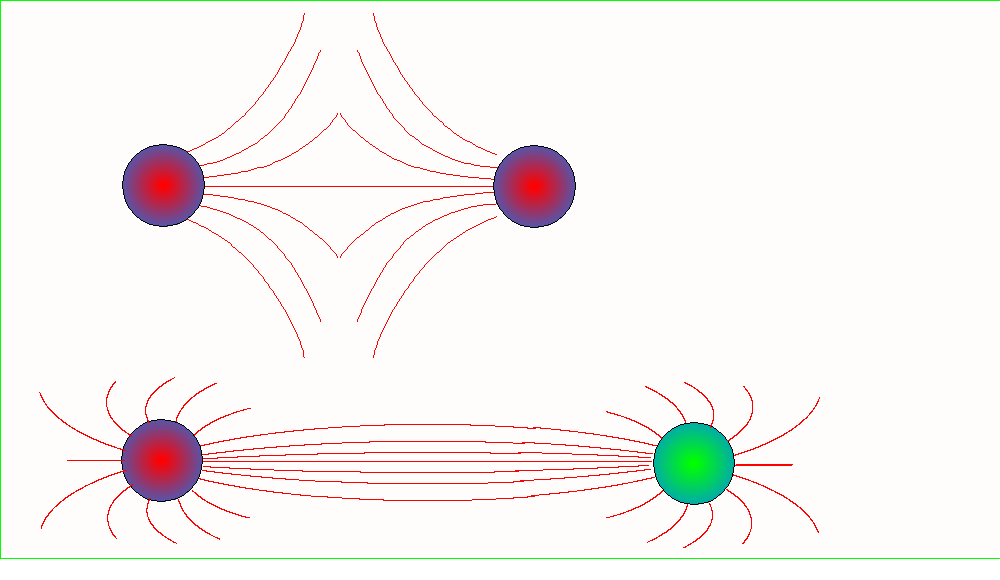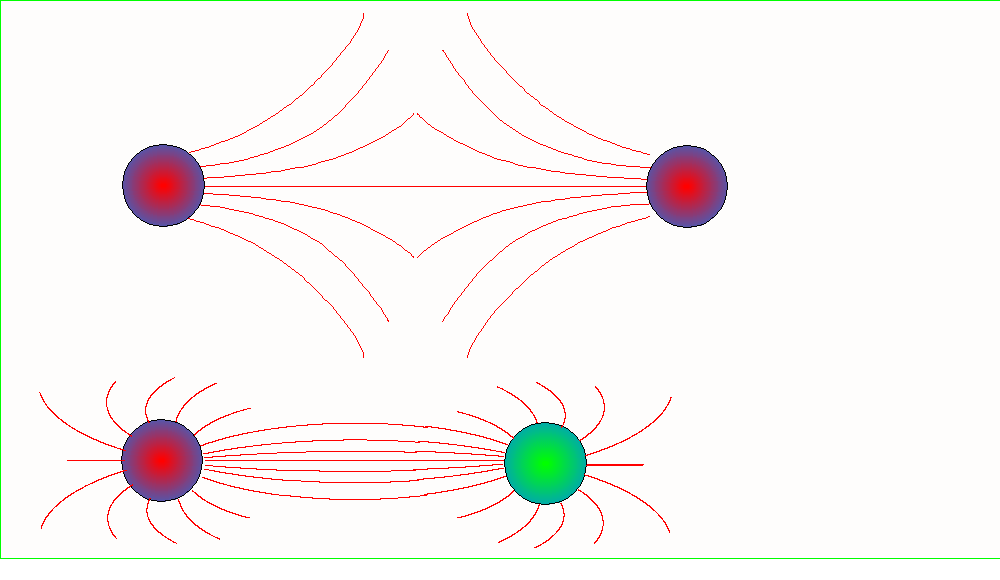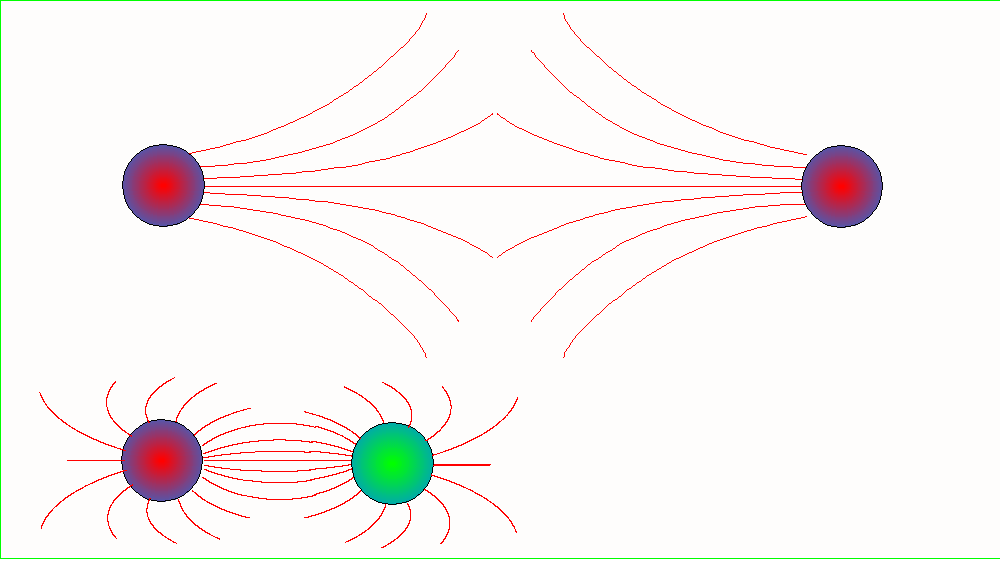Przedstawiając linie sił przyjmuje się konwencję rysunkową, zgodnie z którą gęstość linii sił jest proporcjonalna do natężenia pola w tym miejscu. Linie sił pola w otoczeniu układu dwóch ładunków punktowych, dodatniego i ujemnego o jednakowej wartości bezwzględnej są przedstawione na rysunku:

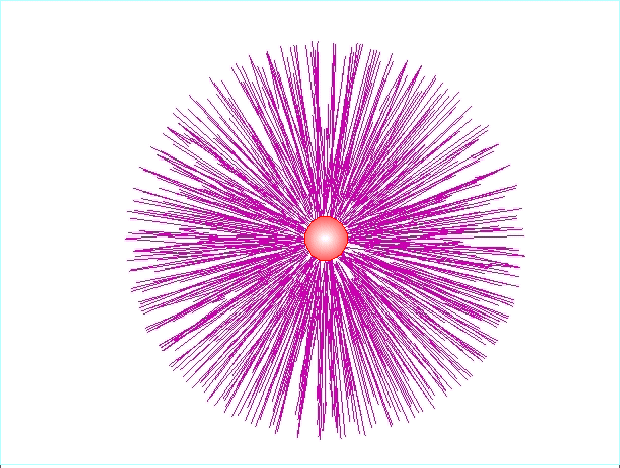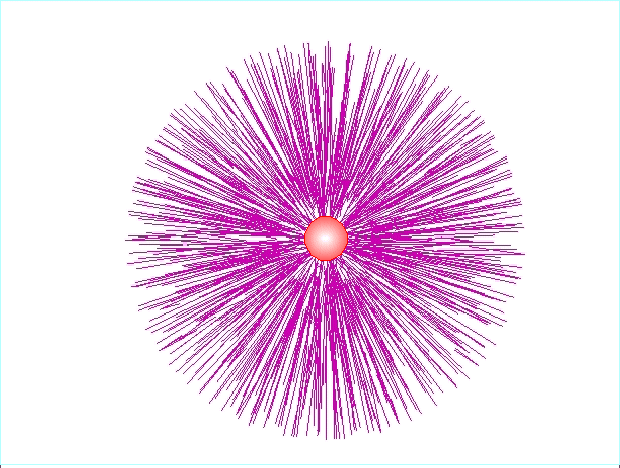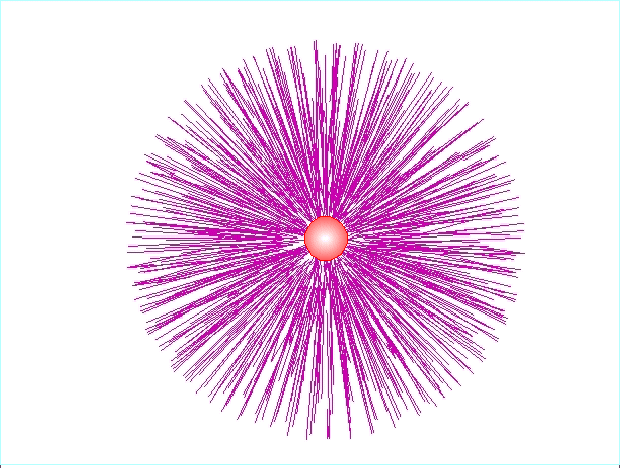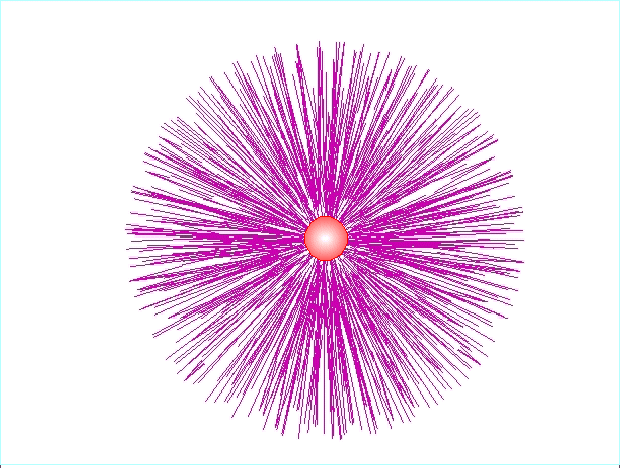
Pojedynczy ładunek umieszczony w próżni jest otoczony radialnym układem linii sił.

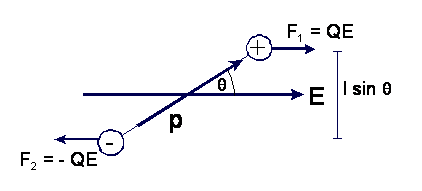
Dipol elektryczny jest sztywnym układem dwóch ładunków punktowych +Q i -Q odległych od siebie o l. Dipol umieszczamy w jednorodnym polu elektrycznym E tak, że wektor E tworzy kąt θ z linią łączącą oba ładunki, zwaną osią dipola. Siła F₁ = QE jest skierowana w kierunku pola, zaś siła F₂ = - QE w kierunku przeciwnym. Obie te siły tworzą parę sił tworzącą moment siły

Iloczyn Ql ładunku Q i odległości l jest nazywany momentem dipolowym. Wektor momentu dipolowego jest skierowany od ładunku ujemnego do dodatniego (odwrotnie niż to jest dla linii sił pola).

Moment siły działający na dipol wyrażamy w postaci iloczynu wektorowego

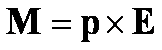
Wartość tego wektora wynosi oczywiście

Jeżeli pole elektryczne nie jest jednorodne, wtedy na dipol działa nie tylko moment skręcający, ale także pewna siła wypadkowa. Powodem tego jest fakt, że oba ładunki dipola znajdują się w polach o nieco odmiennych natężeniach i siły działające na te ładunki nie równoważą się.

Niezerowy elektryczny moment dipolowy mają takie molekuły, jak H₂O, CO, ...

Molekuły symetryczne, np. O₂, N₂, H₂, ... nie mają trwałych momentów dipolowych.

Jednostką momentu dipolowego w układzie SI jest C·m (kulomb · metr). Ponieważ jest to bardzo duża jednostka, to w literaturze stosuje się zwykle jednostkę o nazwie debaj (D), która pochodzi z układu CGS.

1D = 3.338×10^-30 C·m

Dwa ładunki elementarne (równe ładunkom elektronu lub protonu) oddalone od siebie na odległość 1 angstrema tworzą moment dipolowy o wartości

p = 1.602×10^-19 C ·1·10^-10 m = 16.02×10^-30 C·m = 4.8 D.

Zadanie na zastosowanie addytywności wektorowej pól. Znaleźć pole elektryczne E wytwarzane przez dipol. Dla uproszczenia znajdziemy to pole w płaszczyźnie prostopadłej do osi dipola i przechodzącej przez jej środek

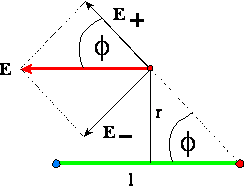
Pola pochodzące od ładunków dodatniego i ujemnego oznaczamy odpowiednio przez E₊ i E-. Suma wektorowa obu tych pól tworzy pole wypadkowe E = E₊ + E-. Ze względu na symetryczne położenie punktu, w którym badamy pole, długości obu wektorów E₊ i E- są jednakowe:

Pionowe składowe pól E₊ i E- kompensują się, a suma składowych poziomych daje długość E szukanego wektora E:

gdzie p = Ql jest momentem dipolowym dipola. Dla r >> l (daleko od osi dipola) wartość pola E wynosi:

Widzimy, że pole wokół dipola zanika ze wzrostem odległości szybciej (jak 1/r³ ) niż pole wokół pojedynczego ładunku, które zanika jak 1/r².

Back to Index