Back to Index

POTENCJAŁY TERMODYNAMICZNE

MINIMA POTENCJAŁÓW W STANACH RÓWNOWAGI

POTENCJAŁY TERMODYNAMICZNE W PRZEMIANACH FAZOWYCH

GRADIENTY I ZJAWISKA TRANSPORTU

* Potencjały termodynamiczne

* Minima potencjałów termodynamicznych w stanach równowagi

* Potencjały termodynamiczne w przemianach fazowych

* Gradienty i zjawiska transportu

Potencjały termodynamiczne są funkcjami stanu, których zmiana wartości w procesach równowagowych (odwracalnych) przy ustalonych wartościach określonych par parametrów stanu ( T i V, T i P, S i P, S i V itd.) jest równa pracy zredukowanej W*, tzn. całkowitej pracy zmniejszonej o pracę wykonaną na przezwyciężenia ciśnienia zewnętrznego. Zdolność do przekształcania w pracę jest powodem, że te funkcje zostały nazwane potencjałami. Istnieje pewna liczba potencjałów termodynamicznych, które mogą być użyte do opisu zachowania się i stabilności układów termodynamicznych, zależnie od typu nałożonych ograniczeń w układzie. W układzie, który jest izolowany od reszty świata, energia wewnętrzna jest wielkością, która przyjmuje wartość minimalną w stanie równowagi. Jeżeli jednak połączymy nasz układ termicznie, mechanicznie albo chemicznie ze światem zewnętrznym, wtedy minimalizacji podlegają inne potencjały termodynamiczne. Wprowadzimy pięć powszechnie używanych potencjałów termodynamicznych: energia wewnętrzna U, energia swobodna F, entalpia H, entalpia swobodna G i potencjał chemiczny :, a także przedyskutujemy warunki w jakich każdy z nich jest minimalizowany w stanie równowagi. Przedstawione to zostało na schemacie poniżej dla energii wewnętrznej U, energii swobodnej F, entalpii H i entalpii swobodnej (potencjału Gibbsa, funkcji Gibbsa) G. Funkcja :, zwana potencjałem chemicznym, wchodzi w skład potencjałów termodynamicznych w przypadku układów otwartych ze zmienną liczbą molekuł.

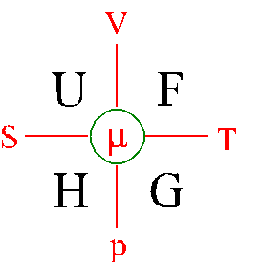
Niezależne S i V: energia wewnętrzna U

Niezależne V i T: energia swobodna F

Niezależne S i p: entalpia H

Niezależne T i p: entalpia swobodna G

1. Niezależne S i V: stała energia wewnętrzna U

Na podstawie pierwszej zasady termodynamiki

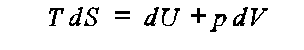
przy S, V = const, mamy dS = 0 oraz dV = 0, zatem

czyli przy ustalonych S i V energia wewnętrzna U jest stała, U = const.

2. Niezależne T i V: stała energia swobodna F (energia swobodna Helmholtza).

Na podstawie pierwszej zasady termodynamiki

przy T, V = const, mamy dV = 0 i możemy napisać

czyli przy ustalonych T i V wielkość F = U - TS jest również stała

Funkcja F jest właśnie energią swobodną. Jej zmniejszenie jest równe pracy wykonanej przez układ

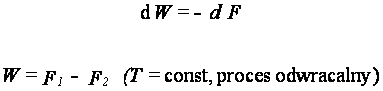
3. Niezależne S i p: stała entalpia H

Na podstawie pierwszej zasady termodynamiki

przy S, p = const, mamy dS = 0 i możemy napisać

czyli przy ustalonych S i p wielkość H = U + pV jest również stała

Funkcja stanu H = U + pV jest nazywana entalpią.

4. Niezależne T i p: stała entalpia swobodna G

Entalpia swobodna jest nazywana także energią swobodną Gibbsa, potencjałem izotermicznym i funkcją Gibbsa.

Na podstawie pierwszej zasady termodynamiki

przy T, p = const możemy napisać

czyli przy ustalonych T i p wielkość G = U + pV - TS jest również stała

Funkcja stanu G = U + pV - TS jest nazywana entalpią swobodną.

5. Zmienna liczba cząstek N: potencjał chemiczny μ

Ciśnienie i temperatura nie są wielkościami addytywnymi. W stanie równowagi ich wartości są takie same w każdej części układu. Takie wielkości nazywane są intensywnymi.

W układach, w których ilość cząstek jest zmienna, szczególne miejsce wśród czterech potencjałów termodynamicznych

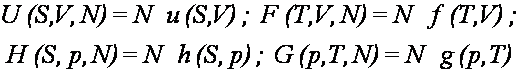
zajmuje entalpia swobodna G. Przyczyna tej osobliwości polega na tym, że potencjał właściwy, czyli g(p, T) okazuje się funkcją jedynie zmiennych intensywnych p i T. Funkcja g(p, T), tj. potencjał termodynamiczny liczony na jedną molekułę, nazywa się potencjałem chemicznym

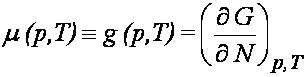
Potencjał chemiczny można także wyrazić jako pochodne pozostałych potencjałów termodynamicznych względem liczby molekuł N.

Na podstawie określenia energii wewnętrznej dla układów otwartych

możemy napisać

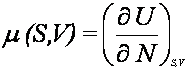
Ponieważ

oraz

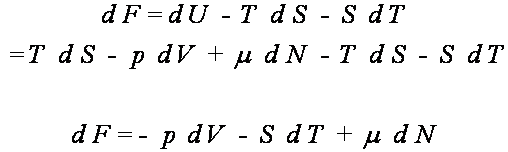
stąd

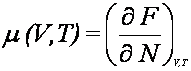
Następnie

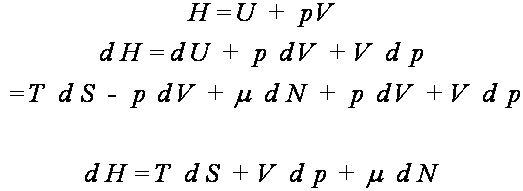
Stąd

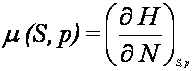
W ten sam sposób

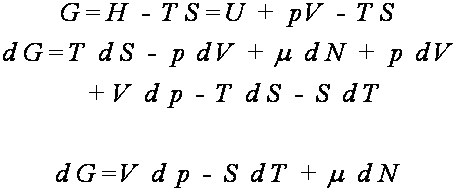
Stąd ponownie

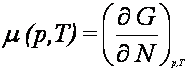
W procesach nieodwracalnych, gdy dQ < TdS, gdy układ zdąża do stanu równowagi przy ustalonej parze parametrów, to odpowiednie potencjały termodynamiczne maleją. Łatwo udowodnić, że po osiągnięciu stanu równowagi potencjały te przyjmują wartości minimalne.

Osiąganie przez potencjały minimum w stanach równowagowych układu przy ustalonej odpowiedniej parze parametrów stanu jest najbardziej użyteczną cechą, ze względu np. na symulacje komputerowe.

Proces osiągania przez potencjały wartości minimalnych opisujemy następująco:

We wszystkich przypadkach posługujemy się własnością entropii

1. Ustalamy S i V - analizujemy U: biorąc pod uwagę, że dS = 0 oraz dV = 0, a następnie dzieląc przez różniczkę czasu dt otrzymujemy

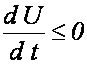
Konkluzja: proces nieodwracalny przebiegający przy stałych S i V prowadzi do stanu równowagi, w którym układ ma minimum energii wewnętrznej U.

2. Ustalamy T i V - analizujemy F: biorąc pod uwagę, że dV = 0, a następnie dzieląc przez różniczkę czasu dt otrzymujemy

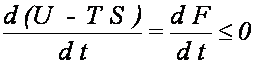
Konkluzja: proces nieodwracalny przebiegający przy stałych T i V prowadzi do stanu równowagi, w którym układ ma minimum energii swobodnej F.

3. Ustalamy S i p - analizujemy H: biorąc pod uwagę, że dS = 0, a następnie dzieląc przez różniczkę czasu dt otrzymujemy

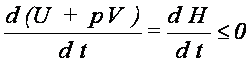
Konkluzja: proces nieodwracalny przebiegający przy stałych S i p prowadzi do stanu równowagi, w którym układ ma minimum entalpii H.

4. Ustalamy p i T - analizujemy G: biorąc pod uwagę, że dS = 0, a następnie dzieląc przez różniczkę czasu dt otrzymujemy

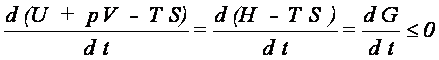
Konkluzja: proces nieodwracalny przebiegający przy stałych p i T prowadzi do stanu równowagi, w którym układ ma minimum entalpii swobodnej G.

Opis termodynamiczny przemian fazowych I-go i II-go rodzaju zwykle jest oparty o analizę energii swobodnej Helmholtza (F) lub energii swobodnej Gibbsa (G). Funkcja Gibbsa G układu pozostaje niezmieniona niezmieniona w każdym procesie, który przebiega w stałej temperaturze i pod stałym ciśnieniem. (G = U – TS + pV, zatem dG = dU – TdS – SdT + pdV + Vdp = Vdp – SdT, ponieważ dU – TdS + pdV = 0). Ponieważ przemiana fazowa zawsze zachodzi przy określonych wartościach tych dwóch parametrów to funkcja G zachowuje ciągłość w czasie tej przemiany.

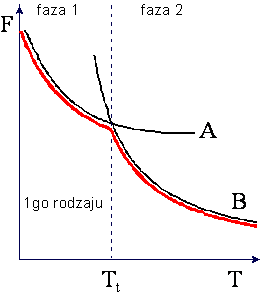
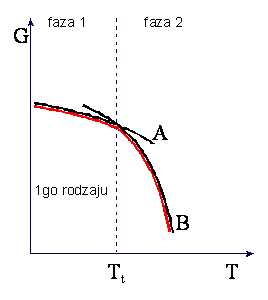
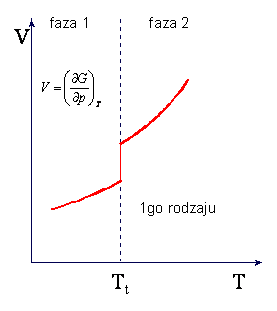
W przemianie fazowej I-go rodzaju zachodząca wtedy zmiana objętości i istnienie ciepła przemiany powodują, że w punkcie przemiany nieciągłe są pochodne

oraz

ponieważ musi wystąpić zmiana entropii S wywołana ciepłem przemiany Q/T. Skoki objętości i entropii w przemianie I-go rodzaju są przedstawione na rysunkach

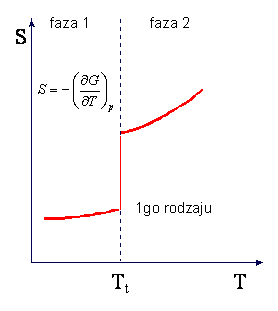
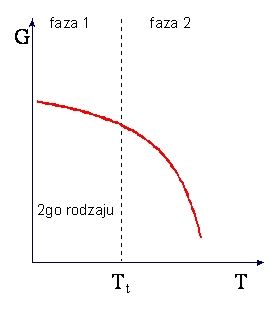
W przemianie fazowej II-go rodzaju nieciągłe są pochodne

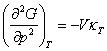oraz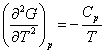

podczas gdy pochodne pierwszego rzędu, -S i V, są ciągłe. W punkcie przemiany II-go rodzaju występuje zmiana tylko w nachyleniu krzywych entropii i objętości w funkcji temperatury podczas gdy nieciągłości występują dla ciepła właściwego i dla izotermicznego modułu objetościowego (κ_T = (naprężenie izotermiczne)/(zmiana objętości)). Charakter zmian entropii i ciepła właściwego w przemianie II-go rodzaju są przedstawione na rysunkach

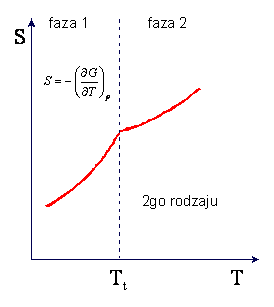
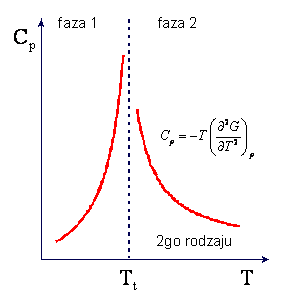
Kształt krzywej ciepła właściwego C_p przypomina grecką literę λ i z tego powodu przemiana II-go rodzaju jest czesto nazywana punktem lambda.

Termin „zjawiska transportu” jest określeniem zbiorczym dla szerokiej klasy przepływów. Dotyczy to zwłaszcza przepływu ładunku elektrycznego (prądu), ciepła, masy (dyfuzja) i pędu (lepkość). Zjawiska transportu występują tylko w stanach nierównowagowych. Kiedy układ osiąga stan równowagi wtedy ustają w nim wszelkie przepływy i przenoszenie np. ładunku i masy odbywa się tylko w wyniku ruchów termicznych i jest tak samo szybkie „w lewo” jak i „w prawo” nie prowadząc do żadnych zmian sumarycznych. Motorem napędzającym każdy transport jest wystąpienie spadków (gradientów) odpowiednich wielkości. Oznacza to, że jeżeli w pewnym miejscu wartość interesującej nas wielkości wynosi Z₁ to w punkcie oddalonym o Δx ta wartość spada do Z₂. Jeżeli ten spadek, ΔZ = Z₂ – Z₁, odbywa się liniowo to stosunek ΔZ/Δx jest równy dokładnie gradientowi wielkości Z, grad Z. Jeżeli ten spadek odbywa się nieliniowo (w dowolny sposób), to gradient określamy jako stosunek odpowiednich różniczek, grad Z = dZ/dx. Ponieważ transport odbywa się w kierunku spadku wielkości Z to ten kierunek jest zgodny z ujemną wartością gradientu, czyli zgodny z „- grad Z”.

Przedstawiony poniżej skrótowy opis poszczególnych zjawisk transportu jest wystarczająco jednoznaczny, ponieważ zastosowano tutaj standardowe oznaczenia wszystkich występujących wielkości.

Transport ładunku (prąd elektryczny)

σ jest przewodnością ośrodka.

Transport ciepła

λ jest współczynnikiem przewodnictwa cieplnego.

Transport masy (dyfuzja)

c - koncentracja, D - współczynnik dyfuzji.

Transport pędu (lepkość)

η - współczynnik lepkości.

Back to Index