Back to Index

PODSTAWY FIZYKI STATYSTYCZNEJ

Prawdopodobieństwo i gęstość prawdopodobieństwa. Wartości średnie.

Rozkład Maxwella. Rozkład Boltzmanna.

* Podstawowe definicje rachunku prawdopodobieństwa

* Prawdopodobieństwa zdarzeń elementarnych

* Kiedy zdarzenia A i B wykluczają się

* Kiedy zdarzenia A i B nie wykluczają się

* Wartość średnia wielkości dyskretnej

* Gęstość prawdopodobieństwa i funkcja rozkładu gęstości prawdopodobieństwa

* Wartość średnia wielkości ciągłej i funkcji wielkości ciągłej

* Rozkład Maxwella

* Rozkład Boltzmanna

Jeżeli spośród wszystkich N zdarzeń losowych (np z całej liczby losowań) znajdziemy N_i zdarzeń pozytywnych (np. wylosowanych czerwonych kul), to prawdopodobieństwo wystąpienia takiego zdarzenia elementarnego P_i określamy jako stosunek

Prawdopodobieństwo P = 1 oznacza absolutną pewność (np. w worku są tylko czerwone kule), natomiast P = 0 oznacza brak jakichkolwiek szans (w worku nie ma ani jednej czerwonej kuli).

Suma wszystkich prawdopodobieństw P_i jest równa 1 (na pewno wyciągniemy jakąkolwiek kulę). Ta równość nosi nazwę warunku normalizacji

Wtedy prawdopodobieństwo wystąpienia jednego z tych zdarzeń jest sumą obu prawdopodobieństw:

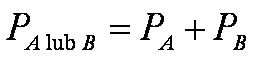
Jeżeli np. co pewien czas odwiedzają nas Andrzej (zdarzenie A) i Beata (zdarzenie B) to prawdopodobieństwo pojawienia się dziś Andrzeja oznaczmy jako P_A, a prawdopodobieństwo odwiedzin Beaty jako P_B. Jeżeli te dwa zdarzenia nawzajem się wykluczają (nie mogą wystąpić łącznie), wtedy prawdopodobieństwo, że odwiedzi nas dziś Andrzej lub Beata, P_{A lub B}, jest sumą obu prawdopodobieństw:

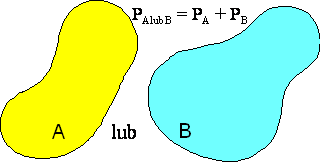
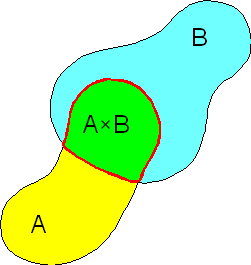
Iloczyn, A × B, jest zbiorem zdarzeń, które należą do A i B łącznie. Jeżeli zdarzenia występują łącznie, to niekoniecznie znaczy, że jednocześnie. Jeżeli, np. w ciągu roku występują średnio trzy trzęsienia ziemi i pięć razy w roku występuje gradobicie to możemy zapytać, jakie jest prawdopodobieństwo tego, że w tym miesiącu wystąpią oba zjawiska (3/12 i 5/12) (niekoniecznie w tym samym dniu).

Jeżeli zdarzenia A i B nie wykluczają się wzajemnie (są od siebie niezależne), to prawdopodobieństwo łącznego wystąpienia obu zdarzeń, czyli prawdopodobieństwo, że dziś odwiedzą nas Andrzej oraz Beata, P_{A oraz B}, jest równe iloczynowi prawdopodobieństw obu zdarzeń

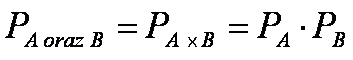
ta reguła jest często stosowana jako definicja niezależności zdarzeń.

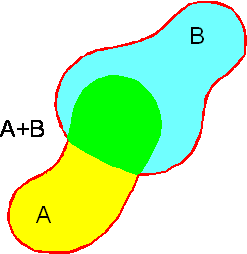
Suma, A+B, jest zbiorem zdarzeń, które należą przynajmniej do jednego zbioru A lub B.

Jeżeli zdarzenia A i B nie wykluczają się wzajemnie, to prawdopodobieństwo wystąpienia któregokolwiek z obu zdarzeń jest mniejsze niż byłoby dla zdarzeń, które się wzajemnie wykluczały.

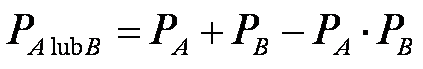
Teraz szansa, że dziś odwiedzi nas Andrzej lub Beata, P_{A lub B}, będzie już mniejsza niż wtedy kiedy te zdarzenia się wykluczały. Oznacza to, że kiedy zdarzenia A i B nie wykluczają się (mogą czasem wystąpić łącznie), to prawdopodobieństwo P_A×B powinno być odjęte od sumy ponieważ obszar A×B był liczony podwójnie w trakcie liczenia P_A + P_B. Jeśli każdy, Andrzej i Beata, odwiedza nas średnio 15 razy w miesiącu i bywa, że niekiedy obaj przychodzą tego samego dnia (nie wykluczają się wzajemnie), to wcale nie jest pewne, że dziś pojawi się któryś z nich a byłoby tak gdyby te zdarzenia się wzajemnie wykluczały.

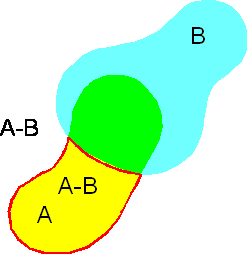
Różnica, A-B, jest zbiorem zdarzeń, które należą do A, ale z wyłączeniem tych, które należą jednocześnie do B.

Jeżeli zdarzenia A i B nie wykluczają się wzajemnie, to prawdopodobieństwo wystąpienia tylko zdarzenia A z wyłączeniem wystąpienia zdarzenia B jest prawdopodobieństwem wystąpienia zdarzenia A zmniejszonym o prawdopodobieństwo jednoczesnego wystąpienia obu zdarzeń:

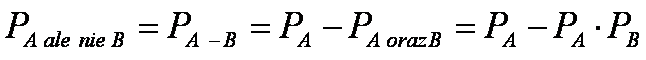
Oznacza to szansę, że dziś odwiedzi nas Andrzej sam, bez Beaty.

Wartość średnia wielkości przyjmującej wartości dyskretne x jest zwykłą średnią ważoną:

Łatwo odpowiedzieć na pytanie, jaka jest szansa znalezienia na Ziemi drzewa o wysokości równej 15 m? Odpowiedź brzmi – żadnej szansy. Dlaczego? Wysokość drzewa jest wielkością ciągłą i sensowne jest tylko pytanie o drzewa, których wysokość zawiera się w pewnym przedziale, np. między 14.9 m a 15.1 m. Jeżeli parametr x ma rozkład ciągły, jak np. wysokość drzewa czy średnica ziarenek piasku na plaży, to rozkład taki powinien być definiowany przez funkcję f(x), zwaną funkcją rozkładu gęstości prawdopodobieństwa. Jeżeli prawdopodobieństwo znalezienia wielkości x w przedziale od x do x+dx wynosi dP(x), to funkcja rozkładu prawdopodobieństwa f(x) jest definiowana równaniem:

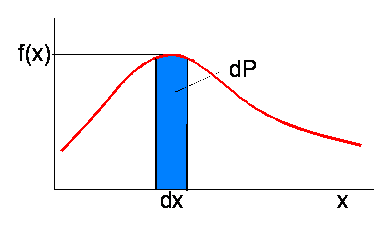
Całkując po całym obszarze zmienności parametru x, otrzymujemy warunek normalizacji prawdopodobieństwa

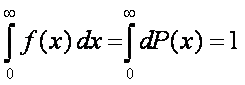
Prawdopodobieństwo, że parametr ciągły x przyjmie wartość z przedziału między A i B wynosi

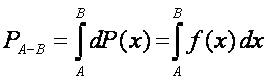
Wartość średnia wielkości przyjmującej wartości ciągłe jest określona przez funkcję rozkładu gęstości prawdopodobieństwa f(x):

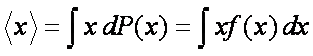
Wartość średnia funkcji tej wielkości ciągłej φ(x) jest także określona przez funkcję rozkładu gęstości prawdopodobieństwa f(x):

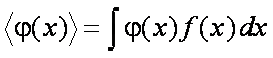
Przykładem funkcji rozkładu gęstości prawdopodobieństwa jest rozkład Maxwella prędkości molekuł oparty na ich energii kinetycznej

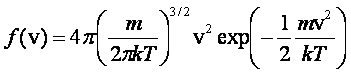
Prawdopodobieństwo znalezienia jakiejś cząstki mającej prędkość w przedziale od v do v + dv wynosi:

Kiedy liczba wszystkich cząstek w układzie wynosi N, to prawdopodobieństwo dP(v) tego, że w przedziale od v do v + dv znajdziemy dN(v) cząstek wyniesie:

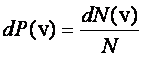
Stąd liczba N₁₂ cząstek, których prędkość jest zawarta między v₁ a v₂ wynosi:

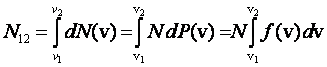
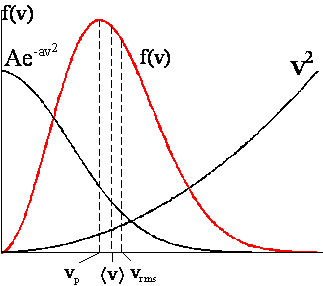
Rozkład Maxwella prędkości molekuł opisujący najbardziej prawdopodobny rozkład prędkości w chaotycznym ruchu molekuł w gazie można przedstawić na wykresie, na którym zaznaczono prędkość najbardziej prawdopodobną v_p, prędkość średnią <v> i średnią prędkość kwadratową v_rms.

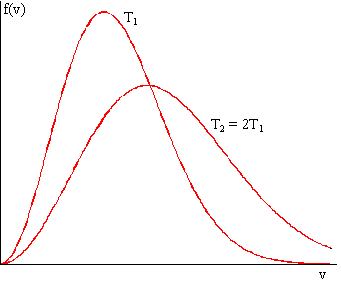
Wraz ze wzrostem temperatury krzywa rozkładu Maxwella ulega „rozmyciu” a charakterystyczne prędkości: najbardziej prawdopodobna v_p, średnia <v> i średnia kwadratowa v_rms są przesunięte w kierunku wyższych wartości.

Rozkład Maxwella jest funkcją rozkładu gęstości prawdopodobieństwa dla prędkości cząstek. Możemy go zatem zastosować do znajdowania wartości średniej prędkości cząstek a również do znajdowania średniej wartości kwadratu tej prędkości czyli wielkości, która określa średnią energię kinetyczną cząstek.

Jeżeli, dla uproszczenia, rozkład Maxwella zapiszemy w postaci

gdzie to wartości średnie i otrzymamy z równań

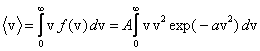
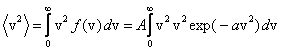
Występująca w obu tych równaniach całka ma rozwiązanie, które może być wyrażone przez funkcję gamma Γ(v) (I. N. Bronsztejn, K. A. Siemiendiajew, Matematyka):

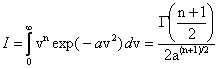
Przy n parzystym (n = 2k) całka ta równa się a przy n nieparzystym (n = 2k + 1) całka równa się . W naszym przypadku n równa się odpowiednio 3 i 4 i na poszukiwaną wartość średnią prędkości otrzymujemy wyrażenie

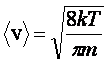
zaś na średnią prędkość kwadratową znajdujemy

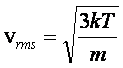
Prędkość najbardziej prawdopodobna jest tą prędkością, dla której krzywa rozkładu Maxwella osiąga maksimum. Ponieważ w tym punkcie df(v)/dv = 0, to przez proste różniczkowanie dostajemy

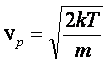
Innym przykładem funkcji rozkładu gęstości prawdopodobieństwa jest rozkład Boltzmanna oparty na energii potencjalnej cząstek (atomów, molekuł elektronów itd.). Rozkład Boltzmanna opisuje zależność liczby molekuł w objętości dV = dx dy dz w punkcie (x, y, z) od ich energii potencjalnej E_p

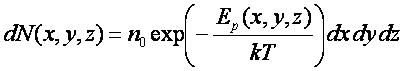
n₀ jest liczbą molekuł w jednostce objętości (gęstością) w miejscu, gdzie ich energia potencjalna jest przyjęta za równą zeru. Inaczej mówiąc, jeżeli gęstość n₀ jest liczbą cząstek w jednostce objętości w miejscu, gdzie ich energia potencjalna jest przyjęta za równą zeru, to gęstość n będąca liczbą cząstek w jednostce objętości w miejscu, gdzie ich energia potencjalna wynosi E_p jest określona przez równanie

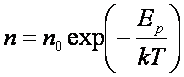
Przykładem zastosowania rozkładu Boltzmanna może być wzór barometryczny, określający gęstość cząstek gazu na wysokości h, gdzie ich energia potencjalna wynosi E_p = mgh:

Back to Index