Back to Index

GAZY RZECZYWISTE

Równanie van der Waalsa. Przemiany fazowe I-go i II-go rodzaju. Reguła faz Gibbsa.

* Gazy rzeczywiste

* Równanie van der Waalsa

* Niektóre inne równania stanu

* Przemiany fazowe I-go i II-go rodzaju

* Reguła faz Gibbsa

Gazy rzeczywiste nie mają już ograniczeń nakładanych na gazy idealne (którymi były brak oddziaływań między cząstkami i brak rozmiarów cząstek).

Ponieważ między cząstkami rzeczywistymi mogą występować różnorodne i często krańcowo skomplikowane oddziaływania wzajemne, a kształt molekuł jest często bardzo złożony, to nie jest możliwe stworzenie jednego uniwersalnego i ścisłego równania stanu. Jak pamiętamy, takie równanie stanu istnieje i ma ono postać

pV = RT

ale obowiązuje ono dla gazu idealnego, który naprawdę nie istnieje. - Nie znamy, niestety, ścisłego równania stanu dla któregokolwiek z gazów rzeczywistych.

Przybliżonym równaniem stanu, które uwzględnia istotne dla gazu rzeczywistego czynniki: oddziaływanie na odległość istniejące między cząstkami (atomami, molekułami) gazu rzeczywistego i ich rozmiary własne jest równanie van der Waalsa:

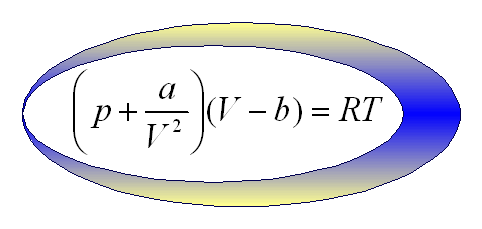
Oddziaływanie między cząstkami jest zawsze przyciągające i gaz rzeczywisty zachowuje się tak, jak gdyby na niego działało dodatkowe ciśnienie a/V², a stała b uwzględnia istnienie objętości własnej molekuł, niedostępnej już dla innych molekuł znajdujących się w tej samej objętości całkowitej V.

Stałe a i b w równaniu van der Waalsa

są dobierane oddzielnie dla każdego konkretnego gazu. Zaletami równania van der Waalsa są jego prostota, oraz fakt, że przewiduje ono wartości krytyczne i to, że można w nim określić odcinki skraplania gazu.

Gaz, w którym cząstki przyciągają się wzajemnie, skupia się bardziej niż wynikało by to z ciśnienia zewnętrznego p i dlatego opisując gaz należy dodać do ciśnienia p dodatkową wartość wynoszącą w tym równaniu a/V².

Gaz rzeczywisty zachowuje się zatem tak, jak gdyby na niego działało dodatkowe ciśnienie. Jednak ciśnienie gazu mierzone na zewnątrz będzie, oczywiście, mniejsze, jak to można pokazać symbolicznie na rysunku.

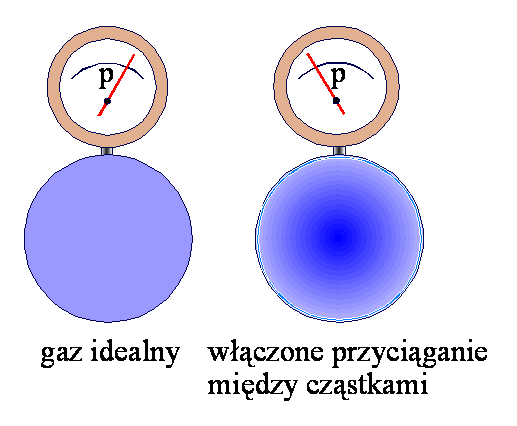
Ciśnienie gazu mierzone na manometrze będzie, oczywiście, mniejsze w przypadku gazu rzeczywistego, podczas gdy w równaniu van der Waalsa przewidujemy ciśnienie większe o czynnik a/V². Postępujemy tak, dlatego, że naszym zadaniem jest opisać zachowanie się gazu a nie manometru.

Izotermy van der Waalsa, czyli wykresy p = p(V) dla temperatur T₁ < T₂ < T₃ .... otrzymane na podstawie równania van der Waalsa mają kształt esowaty.

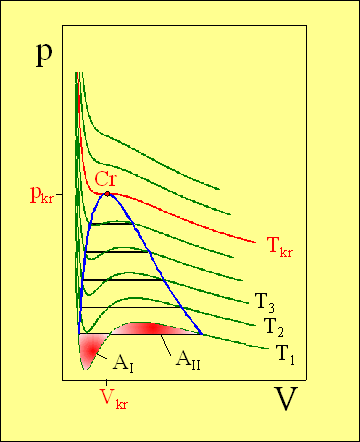
Jest to kształt silnie „niefizyczny” ponieważ przewiduje na pewnych odcinkach zmniejszanie się ciśnienia wraz ze zmniejszaniem się objętości. Okazuje się jednak, że na tych izotermach można poprowadzić odcinki poziome, które obrazują proces skraplania / parowania i odwzorowują prawdziwe, obserwowane eksperymentalnie zachowanie się gazu rzeczywistego. Pola powierzchni A_I i A_II są dla określonej izotermy jednakowe. Punkt krytyczny Cr znajduje się na izotermie krytycznej T_kr i matematycznie jest dla tej izotermy punktem przegięcia.

Widać, że gazu nie można skroplić – niezależnie od przyłożonego ciśnienia – jeżeli jego temperatury nie obniżymy poniżej temperatury krytycznej.

Ponieważ punkt krytyczny Cr znajdujący się na izotermie krytycznej T_kr jest dla tej krzywej punktem przegięcia to oznacza to, że w punkcie krytycznym

oraz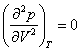

Z tych równań oraz z samego równania van der Waalsa znajdujemy parametry krytyczne T_c, p_c i V_c w postaci

Współczynnik krytyczny dla równania stanu van der Waalsa wynosi

Wartości znalezione eksperymentalnie wahają się od 3.03 dla H₂ do 4 dla dużych molekuł. Stosując parametry zredukowane

otrzymujemy równanie stanu nazywane zredukowanym równaniem stanu

Niektóre inne równania stanu

Pewne równania stanu, inne niż równanie van der Waalsa, znalazły szczególne zastosowania i w pewnych przypadkach dają lepszą zgodność z eksperymentem w ograniczonych zakresach parametrów. Jednakże są one nieodmiennie trudniejsze do matematycznych opracowań.

Równanie Dieterici

przewiduje istnienie punktu krytycznego z , co jest wartością o wiele bliższą do danych eksperymentalnych niż wartość dawana przez równanie van der Waalsa. Jednakże to równanie daje złą zgodność z eksperymentem przy wysokich ciśnieniach.

Równanie Berthelota

,

w którym stała a’ jest niezależna od temperatury. Równanie to jest szczególnie wygodne w zastosowaniach do gazów i par w niskich temperaturach.

Równanie Callendara wprowadzone wyłącznie dla wody i nie przewidujące punktu krytycznego

Przemiany fazowe są szczególnego rodzaju procesami termodynamicznymi, w których zmiana stanu układu jest połączona ze zmianą fazy substancji tworzącej ten układ. Proces skraplania gazu rzeczywistego, o którym mówiliśmy przy okazji równania van der Waalsa, jest przykładem przemiany fazowej chociaż samo równanie van der Waalsa nie przewiduje skraplania i odcinki izoterm odpowiadające skraplaniu wprowadziliśmy na podstawie danych eksperymentalnych.

Wszystkie, dobrze znane z życia codziennego zmiany stanu skupienia, jak

parowanie skraplanie

sublimacja osadzanie

topnienie krystalizacja

noszą nazwę przemian fazowych I-go rodzaju.

Przemiana fazowa I-go rodzaju zachodzi wtedy, gdy w tym procesie obserwuje się:

- Niezerowe ukryte ciepło (entalpia) przemiany;

- Występowanie nukleacji (zarodnikowania nowej fazy), czyli że przemiana nie zachodzi w całej objętości jednocześnie;

- Istnienie zjawisk “prze” (przechłodzenia i przegrzania).

Najlepiej znanymi przykłada przemian fazowych I-go rodzaju są powszechnie znane zmiany stanu skupienia : parowanie, skraplanie, topnienie, krystalizacja.

Zjawiska przemian fazowych są rezultatem powszechnej w przyrodzie tendencji każdego układu do osiągnięcia stanu, w którym energia tego układu jest najmniejsza.

Wygodnym do analizy przemian fazowych rodzajem energii jest tzw. energia swobodna F = U - TS, czyli energia, która w całości może zostać zamieniona na pracę. Entropia S zostanie omówiona później w kontekście II. zasady termodynamiki.

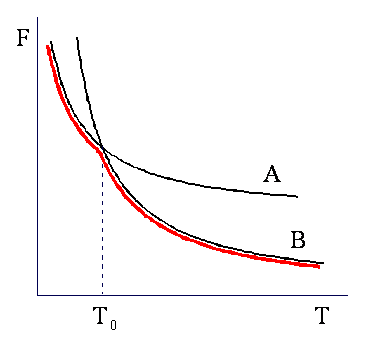
Wykresy energii F w funkcji temperatury dla dwóch stanów układu A i B są przedstawione czarnymi liniami. W niższej temperaturze stabilny – wygodniejszy energetycznie - jest stan A (ma niższe F), a w wyższej stabilny jest B (teraz on ma niższe F). W czasie ogrzewania układ przesuwa się po czerwonej linii.

W temperaturze T₀ zachodzi przemiana fazowa ze stanu A do B. W tym punkcie energie swobodne obu faz są jednakowe: F_A = F_B. W całym procesie ogrzewania układ przyjmuje najniższą dopuszczalną dla niego wartość energii swobodnej.

Fazy, jakie może przyjmować układ, wygodnie jest przedstawiać na diagramach fazowych w układzie temperatura – ciśnienie p-T:

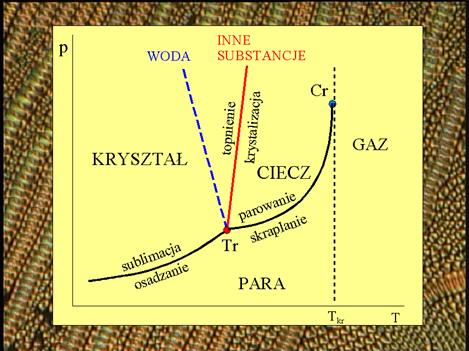
W punkcie krytycznym Cr zanika różnica między gazem a cieczą. Proszę zwrócić uwagę na odmienne nachylenie linii topnienie – krystalizacja dla wody.

Zupełnie inny charakter mają przemiany fazowe II-go rodzaju. Nie mają one żadnej z cech przemian I-go rodzaju.

W przemianie fazowej II-go rodzaju NIE obserwuje się:

- Niezerowego ukrytego ciepła (entalpii) przemiany;

- Nukleacji (zarodnikowania nowej fazy), czyli że przemiana zachodzi w całej objętości jednocześnie;

- Zjawisk “prze” (przechłodzenia i przegrzania).

W temperaturze, w której zachodzi przemiana fazowa II. rodzaju nie ma zmiany stanu skupienia, a występuje tylko zmiana symetrii układu. Przykładami przemian fazowych II-go rodzaju są:

Przemiana typu porządek-nieporządek w stopach

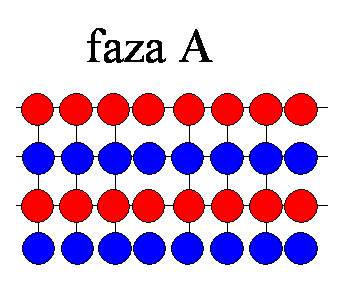
W niskiej temperaturze atomy obu rodzajów rozłożone są w oddzielnych warstwach („porządek”)

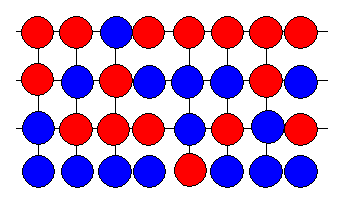
W wyższej temperaturze ten porządek ulega zaburzeniu – niektóre atomy czerwone i niebieskie wymieniają się swoimi położeniami w sieci chociaż ciągle prawdopodobieństwa ich znajdowania w poszczególnych warstwach nie są jednakowe. Jest to zaburzona faza A.

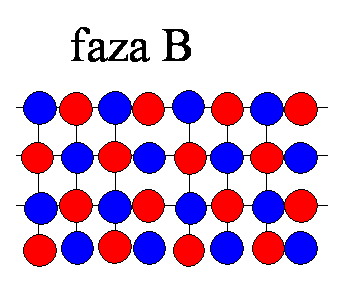
W jeszcze wyższej temperaturze oba rodzaje atomów zostają całkowicie wymieszane („nieporządek”). Prawdopodobieństwa znalezienia w określonym węźle atomu czerwonego i niebieskiego są jednakowe. Jest to faza B.

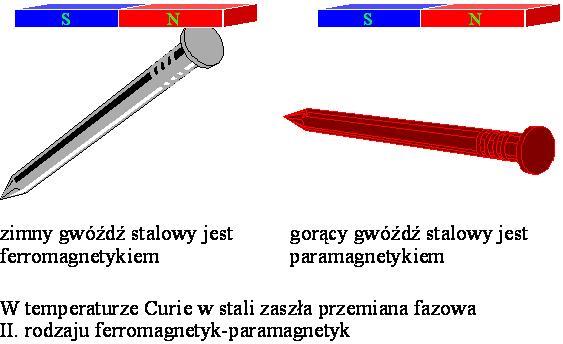
Przemiana ferromagnetyk ↔ paramagnetyk

Bardzo gorący gwóźdź stalowy nie jest przyciągany przez magnes

Przemiana przewodnik ↔ nadprzewodnik

Prąd elektryczny raz wzbudzony w pierścieniu nadprzewodzącym będzie w nim płynął praktycznie bez końca. O płynącym prądzie świadczy wytwarzane przez niego pole magnetyczne B.

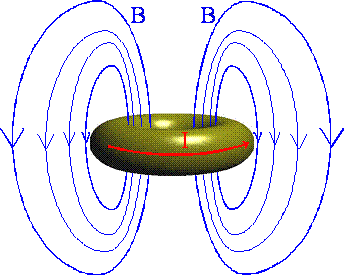
Pole magnetyczne nie wnika w nadprzewodnik, co powoduje lewitację nad nim magnesu (efekt Meissnera).

Przemiana ciecz lepka ↔ ciecz nadciekła.

W bardzo niskich temperaturach, 1 – 2 K i niższych w okolicy zera bezwzględnego, niektóre ciecze, jak hel, przechodzą w stan nadciekły.

Jednym z wielu zjawisk obserwowanych w cieczach nadciekłych jest samorzutne wypełzanie tych cieczy ze zbiorników.

Cenną wskazówką na temat zależności między liczbą składników w układzie C (components), liczbą faz współistniejących w danym stanie P (phases), a liczbą stopni swobody F (degrees of freedom) jest reguła faz Gibbsa. Reguła ta jest przydatna przy przewidywaniu zachowania się układów bardziej złożonych:

F + P = C + 2

F - liczba stopni swobody, oznacza ilość parametrów (p, V, T, ...), które mogą być zmienione bez miany stanu równowagi układu,

P - liczba współistniejących w układzie faz, czyli tych części, które są odseparowane od innych granicą rozdziału faz (np. roztwór wody i soli jest jedną fazą ale nadmiar soli wraz z graniczącym roztworem stanowią dwie fazy),

C - liczba składników (rodzajów istniejących związków chemicznych) w układzie.

Może być interesujące, że bardzo podobną postać ma słynny wzór Eulera-Kartezjusza dla wielościanów

V + F = E + 2

V jest liczbą wierzchołków wielościanu,

F - liczbą jego ścian,

E - liczbą jego krawędzi

Back to Index