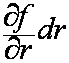Back to Index

ENERGIA WEWNĘTRZNA

I. prawo (zasada) termodynamiki. Ciepła właściwe

* Energia wewnętrzna

* I. prawo (zasada) termodynamiki

* Praca przy zmianie objętości gazu idealnego

* Ciepła właściwe

Energią wewnętrzną U nazywamy sumę wszystkich rodzajów energii w układzie: energii kinetycznej ruchu atomów i molekuł, energii potencjalnej oddziaływań między nimi, ale też energii makroskopowych, np. energii deformacji kryształu itd. Nie obejmuje on energii kinetycznej i potencjalnej układu jako całości ani energii jądrowych czy energii wewnątrzatomowych. Wartość całkowitej energii wewnętrznej układu w jakimkolwiek szczególnym stanie nie może być zmierzona. Istotną wielkością jest zmiana energii wewnętrznej ΔU. W układzie zamkniętym zmiana energii wewnętrznej ΔU jest równa ciepłu Q dostarczonemu do tego układu zmniejszonemu o wartość pracy W wykonanej przez układ na swoim otoczeniu,

Wyżej zapisane równanie stanowi najprostsze sformułowanie I. zasady termodynamiki. Zgodnie z pierwszym prawem termodynamiki, ciepło Q dostarczone do układu idzie na wykonanie przez ten układ pracy W oraz na zmianę jego energii wewnętrznej ΔU.

Pierwszą zasadę termodynamiki zapisujemy zwykle w ścisłej postaci różniczkowej:

Poprzeczne kreski na znaku różniczki, đ, są użyte dla przypomnienia, że W i Q nie są funkcjami stanu (czyli nie są funkcjami parametrów stanu, takich jak p, V, T, n, S). Wielkości đQ i đW są jedynie pewnymi nieskończenie małymi zmianami Q i W. Energia wewnętrzna U jest funkcją stanu i dlatego dU reprezentuje różniczkę zupełną. Ogólnie, różniczka zupełna funkcji f(r, s, w) oznacza wyrażenie

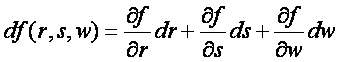
gdzie pochodną cząstkową, np. ∂f/∂r, należy rozumieć jako podatność (czułość) funkcji f na zmiany zmiennej r. Sens poszczególnych członów w określeniu różniczki zupełnej jest przedstawiony w tabeli poniżej.

Czułość funkcji f(r, s, w) na zmiany zmiennej r:	Wartość zmiany zmiennej r:
Nieskończenie mały przyrost funkcji f(r, s, w) jako rezultat zmiany zmiennej r:

Praca dW wykonana przez gaz przy przesunięciu tłoka, mającego powierzchnię A, o mały odcinek dl jest równa

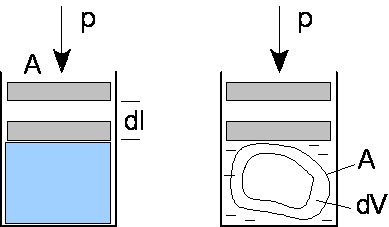
Dla skończonych zmian objętości od V₁ do V₂ praca wykonana przez gaz wyniesie

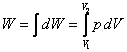
Tak więc, pierwsza zasada termodynamiki może być zapisana w postaci

Znając I. zasadę termodynamiki wiemy już, że nie jest możliwe zbudowanie maszyny, którą nazwano perpetuum mobile (wieczny ruch) pierwszego rodzaju.

Taka maszyna, raz uruchomiona, miałaby poruszać się nieskończenie długo i wykonywać w tym ruchu użyteczną pracę bez zasilania w energię ze źródła zewnętrznego. Maszyna taka łamałaby jednak I. zasadę termodynamiki, a zatem jej zbudowanie jest niewykonalne. Zanim koncepcja energii i jej zachowania zostały powszechnie zrozumiałe, bardzo wielu wynalazców traciło lata swego życia na bezowocne poszukiwania luki w prawach natury, która pozwoliłaby na stworzenie perpetuum mobile.

Restrykcje wprowadzone przez termodynamikę idą jeszcze dalej. Druga zasada termodynamiki, jak dowiemy się nieco później, nie pozwala także na zbudowanie perpetuum mobile drugiego rodzaju czyli maszyny, która całe dostarczone ciepło zamieniłaby w inną postać energii (np. na pracę).

Ciepło właściwe C definiujemy ogólnie jako

Kiedy ogrzewanie jest prowadzone przy stałej objętości, wtedy

Praca wykonana przez gaz idealny jest przy stałej objętości równa zeru a ciepło właściwe przy stałej objętości V oznaczamy jako

Stwierdziliśmy zatem, że zmiana energii wewnętrznej jednego mola gazu jest równa

Ponieważ energia wewnętrzna jednego mola gazu idealnego (n = 1) wynosi

to ciepło właściwe gazu przy stałej objętości jest równe

Ciepło właściwe przy stałym ciśnieniu definiuje się w ścisłym sformułowaniu jako pochodną

gdzie H = U + pV nosi nazwę entalpii, która została wprowadzona dla uwzględnienia tej części dostarczonego ciepła, jaka pójdzie na wykonanie pracy związanej z rozszerzeniem ogrzewanego ciała (pV).

Wyrażenie zmiany energii wewnętrznej dU przez ciepło właściwe CV i zmianę temperatury dT prowadzi do nowego sformułowania I. prawa termodynamiki

Po podzieleniu obu stron równania przez dT, mamy

Ponieważ V = RT/p, to znajdujemy dla jednego mola gazu

Tworzymy wielkość κ = C_p/C_V, zwaną wykładnikiem adiabaty

Energię wewnętrzną możemy teraz wyrazić jako

Back to Index