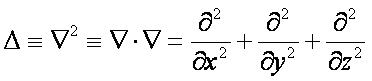DYNAMIKA

FUNKCJE WEKTOROWE

Operator nabla. Gradient. Dywergencja. Rotacja.

Jeżeli w każdym punkcie pewnego obszaru dwu- lub trójwymiarowego istnieje określony wektor, np. natężenia pola grawitacyjnego czy natężenia pola elektrycznego lub wektor siły wywieranej przez te pola, to taki obszar nazywamy polem wektorowym.

W odróżnieniu od pola wektorowego istnieje także pojęcie pola skalarnego. W tym przypadku każdemu punktowi przypisujemy pewna wartość wielkości skalarnej. Przykładami pól skalarnych mogą być pole temperatur, pole gęstości lub pole natężenia dźwięku czy światła.

Jeżeli w każdym punkcie pola wektorowego wektory są jednakowe, czyli mają te same długości, kierunki i zwroty, to mówimy, że takie pole jest jednorodne.

Również pola skalarne, podobnie jak wektorowe, mogą być jednorodne lub niejednorodne. Jednorodnym pole skalarnym nazywamy takie pole, w którym wartość skalara jest taka sama.

Najbardziej interesujące i użyteczne zjawiska pojawiają się w polach niejednorodnym obu rodzajów. Do opisu konfiguracji pól niejednorodnych służą tzw. funkcje wektorowe: GRADIENT, DYWERGENCJA i ROTACJA.

Funkcje wektorowe: GRADIENT, DYWERGENCJA i ROTACJA są określone za pomocą operatora różniczkowego zwanego NABLA .

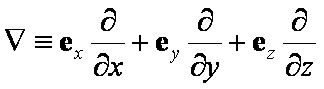
Gradient wielkości wektorowej lub skalarnej oznacza spadek lub narastanie tej wielkości w określonym kierunku. Gradient wielkości wektorowej jest matematycznie tensorem, wspaniałym narzędziem do opisu zjawisk przebiegających w ośrodkach niejednorodnych (anizotropowych). Tensory stanowią jednak zagadnienie zbyt obszerne i zaawansowane na to, aby je można tutaj przedstawić. Niech przykładem będzie gumowa membrana, rozpięta na jakiejś ramce i odkształcona przez nacisk palca. Kształt takiej odkształconej membrany może być opisany tylko przy użyciu tensora. Dla nas najbardziej istotne będzie działanie gradientów (spadków) wielkości skalarnych. Od wartości tych gradientów zależą tzw. zjawiska transportu: transport ładunku ( prąd elektryczny), transport ciepła (przewodnictwo cieplne), transport masy (dyfuzja) i transport pędu (lepkość).

Gradient wielkości skalarnej jest wektorem, jaki powstaje przez działanie operatora nabla na wielkość skalarną φ(x, y, z) będącą funkcją współrzędnych x, y i z.

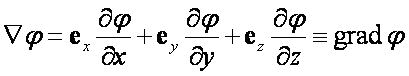
Dywergencja jest wielkością skalarną, będąca produktem iloczynu skalarnego nabli i wektora A(x, y, z)

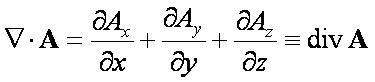
Termin „dywergencja” oznacza „wypływ, wydajność, rozbieżność” pola wektorowego.

Rotacja jest wielkością wektorową, będąca produktem iloczynu wektorowego nabli i wektora A(x, y, z)

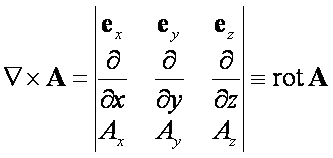
Rotacja opisuje wirowość pola wektorowego, czyli regularną zmianę jego kierunku od punktu do punktu.

Składowe wektora rotacji znajdujemy podobnie jak składowe każdego innego iloczynu wektorowego.

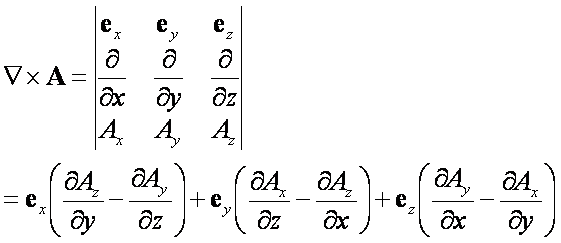
Prąd elektryczny jest wywołany przez GRADIENT potencjału elektrycznego. Najważniejszymi prawami przyrody rządzącymi wszystkimi zjawiskami w dziedzinach elektrodynamiki i optyki są równania Maxwella, których postać różniczkowa jest wyrażona przez DYWERGENCJĘ i ROTACJĘ

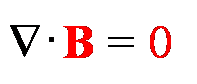
Dla dociekliwych:

Operator Laplace’a, czyli laplasjan, jest operatorem różniczkowym powstającym z iloczynu skalarnego dwóch operatorów nabla:

Laplasjan w cylindrycznym układzie odniesienia:

Laplasjan w sferycznym układzie odniesienia:

Back to Index