HYDRODYNAMIKA

Równanie Bernoulli’ego.

* Proste demonstracje prawa Bernoulli’ego

Płynami nazywamy ciecze i gazy. Hydrodynamika opisuje zjawiska związane z przepływem płynów, przy czym ścisły opis tych zjawisk jest ograniczony do przepływów laminarnych. Przepływ laminarny (warstwowy) występuje wtedy, gdy strumień płynu można podzielić w myśli na układ równoległych do siebie warstewek przesuwających się po sobie i gdy ten układ nie ulega zaburzeniu mimo zmiany kierunku strumienia. Na fotografii pokazano przepływ laminarny w symetrycznym opływie profilu przez płaski strumień. Linie strumienia były uwidocznione za pomocą zabarwionej cieczy wprowadzanej od góry strumienia. (Milton Van Dyke, An Album of Fluid Motion, The Parabolic Press, Stanford, CA, 1982).

Rozkład prędkości w płynie przepływającym laminarnie w rurze jest pokazany na rysunku.

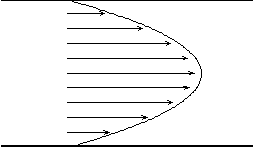
Po przekroczeniu pewnej prędkości granicznej ruch płynu przechodzi w przepływ turbulentny, w którym strumień płynu zostaje rozbity na szereg wirów. Każdy z takich wirów jest złożony z jeszcze mniejszych wirów i ten podział może być prowadzony do obszarów zawirowań o coraz mniejszych rozmiarach. Ten skomplikowany ruch płynu nie ma wystarczająco ścisłego opisu teoretycznego. Na fotografii pokazano tworzenie się turbulentności przy przepływie przez siatkę. Nitki dymu demonstrują przechodzenie jednorodnego laminarnego strumienia przez otwory siatki. Pojawiające się niestabilności przesuwanych warstw prowadzą do rozwinięcia się turbulentności wzdłuż strumienia. (Milton Van Dyke, An Album of Fluid Motion, The Parabolic Press, Stanford, CA, 1982).

Pojawienie się turbulencji może być scharakteryzowane w przybliżony sposób przez bezwymiarową tzw. liczbę Reynoldsa, Re:

dla płynu o gęstości ρ i lepkości η przepływającego w rurze o promieniu r ze średnią prędkością . Krytyczną wartością jest w przybliżeniu Re = 2300 (poniżej tej wartości - przepływ laminarny, powyżej - turbulentny).

Bardzo ważną cechą charakteryzującą przepływ jest lepkość płynu η określająca wartość siły F, jaką należy przyłożyć do płytki, jak na rysunku, aby nadać jej stałą prędkość v. Między ruchomą płytką o polu powierzchni A i równoległym do niej stałym podłożem znajduje się warstewka płynu o grubości h.

Jeżeli spadek prędkości płynu może być traktowany jako liniowy, to wtedy

W innych przypadkach należy stosować wzór bardziej ogólny:

W opisie przepływu płynów często wykorzystywane jest równanie ciągłości, które nie oznacza nic innego jak tylko fakt, że strumień płynu nie jest rozgałęziony i przez każdy jego przekrój przepływa w jednakowym czasie jednakowa masa płynu (m₁ = m₂ = ...). Dla dwóch dowolnych przekrojów strumienia równanie ciągłości można zapisać w postaci

Dla cieczy nieściśliwej (gdy jej gęstość ρ nie ulega zmianie) równanie ciągłości jest szczególnie proste

Skos: RÓWNANIE BERNOULLI’EGO

Jedno z najbardziej interesujących równań, pozwalających zrozumieć całe bogactwo zjawisk mechanicznych w płynach, czyli w cieczach i gazach, wynika tylko z zastosowania uniwersalnej zasady zachowania energii. Równanie to nosi nazwę równania Bernoulli’ego i jest wynikiem analizy tylko energii mechanicznej w płynach: energii kinetycznej, energii potencjalnej i pracy wykonanej z udziałem tych energii. Zjawiska przewidywane przez równanie Bernoulli’ego i obserwowane w prostych eksperymentach są bardzo często zupełnie zaskakujące i sprzeczne z potocznym, intuicyjnym przewidywaniem skutków wydarzeń.

Stosowanie równania Bernoulli’ego jest podstawą wielu gałęzi przemysłu przynoszących produkt wart setek miliardów dolarów. Najpowszechniej znany jest przemysł lotniczy i transport lotniczy. Siła nośna skrzydeł samolotów, chociaż w rzeczywistości jest uwarunkowana wielu skomplikowanymi czynnikami, to u jej podstaw leży bezpośrednie działanie równania Bernoulli’ego.

Fragment skrzydła z silnikami samolotu Airbus A330, który

zawiózł autora z Frankfurtu do Denver, Colorado, USA w sierpniu 2008.

Aby otrzymać równanie Bernoulli’ego przeprowadzimy prostą analizę energii i pracy dla strumienia płynu w płynącego w rurze. Aby analiza miała cechy ogólności, rura ma zmienny przekrój i nie jest położona poziomo. W ciągłym strumieniu płynu (cieczy lub gazu) wybieramy dwa dowolne jego odcinki zawierające tę samą masę m płynu. Środki masy obu odcinków znajdują się na wysokościach h₁ i h₂, zaś pola przekrojów poprzecznych strumieni, ciśnienia i prędkości płynu wynoszą na tych odcinkach odpowiednio A₁ i A₂, p₁ i p₂ oraz v₁ i v₂ .

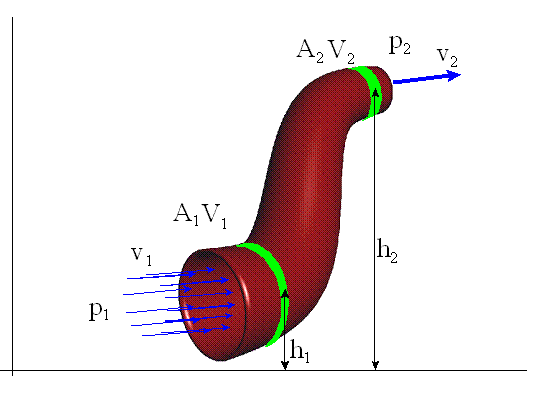
Suma energii kinetycznej, energii potencjalnej i pracy wykonanej przez płyn jest jednakowa na każdym z tych odcinków

czyli

Ponieważ odcinki zostały wybrane dowolnie, to ta suma musi być stała w dowolnym miejscu przekroju. Zatem

Na podstawie równania ciągłości za masę m przyjmujemy m = ρV i dzielimy równanie przez V. W rezultacie znajdujemy równanie Bernoulliego w postaci

opisujące ciśnienia na każdym przekroju strumienia. Na podstawie zasady, że nie można dodawać stokrotek do kóz, każdy ze składników sumy musi mieć ten sam wymiar. Tutaj wyrazy mają wymiar ciśnienia; pierwszy reprezentuje ciśnienie dynamiczne, drugi - hydrostatyczne, a trzeci - ciśnienie statyczne.

Rzadko kiedy zdarza się sytuacja, w której istotną rolę odgrywa wysokość h. Dlatego zazwyczaj wystarcza stosować prostą formę równania Bernoulli’ego:

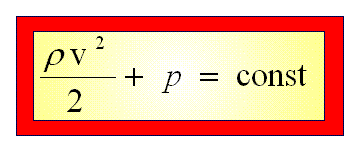
Należy pamiętać, że równanie Bernoulli’ego w otrzymanej przez nas postaci jest słuszne jedynie dla płynu nieściśliwego (dla stałego ρ).

Proste demonstracje działania prawa Bernoulli’ego.

1. Jedną z nich jest zmiana ciśnień w wodzie płynącej w rurkach o stałym i zmiennym przekroju. Spadek ciśnienia w rurce o stałym przekroju jest liniowy, podczas gdy w rurce, w której wytworzono zatokę i przewężenie widać, że w „wąskim gardle” ciśnienie płynu nie rośnie, ale wręcz odwrotnie – maleje. W „zatoce”, gdzie prędkość wody jest mała, ciśnienie jest bardzo wysokie.

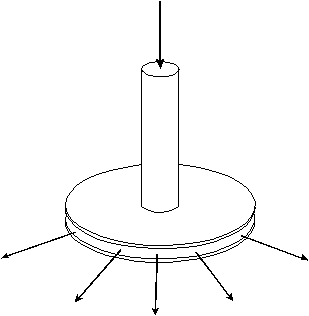
2. Przepływ płynu (np. sprężonego powietrza) między dwiema płytami metalowymi nie powoduje rozepchnięcia płyt, ale wręcz odwrotnie – przywieranie ich do siebie. Zjawisko zostało nazwane paradoksem hydrodynamicznym.

3. Przejawem działania prawa Bernoulli’ego jest efekt Magnusa, przedstawiony na rysunku dla cylindra rotującego w przepływającej cieczy i dla “podkręconej” piłki futbolowej.

Jeżeli cylinder będzie obracany w nieruchomym płynie, to otaczające cylinder warstwy płynu uzyskują prędkość v_s. Gdy teraz uruchomimy płyn z prędkością v_f, to w otoczeniu cylindra przepływająca ciecz będzie porywana przez ruchomą jego powierzchnię i będzie spowalniana u góry (v_g = v_f - v_s ), zaś przyśpieszana na dole (v_d = v_f + v_s ). Jeżeli ciśnienia górne i dolne oznaczymy odpowiednio przez p_g i p_d, to z prawa Bernoulli’ego otrzymamy

Dlatego p_g > p_d i siła Magnusa jest skierowana w dół. Podobne rozumowanie możemy przeprowadzić dla “podkręconej” piłki.

Skos: POWSTAWANIE SIŁY NOŚNEJ

Pojawienie się zasadniczej składowej siły nośnej skrzydeł samolotów i latawców

Teoria siły nośnej skrzydła samolotu jest zagadnieniem bardzo złożonym i nie może być tutaj przedstawiona. W przyjętym tutaj opisie zaniedbujemy przede wszystkim ściśliwość powietrza i turbulencje przepływu. O wartości siły nośnej decydują dwa główne zjawiska:

a. Różnica ciśnień powietrza nad górną powierzchnią skrzydła i pod jego dolną powierzchnią wywołana przez niesymetryczne wyprofilowanie obu tych powierzchni i opisywana przez prawo Bernoulli’ego. Ta różnica ciśnień jest wywołana różnicami prędkości obu strug powietrza, górnej i dolnej, które opływają odpowiednio wyprofilowane skrzydło. Wypukłość górnej powierzchni skrzydła powoduje, że prędkość powietrza nad skrzydłem jest większa niż pod skrzydłem. Zgodnie z uproszczonym prawem Bernoulli’ego

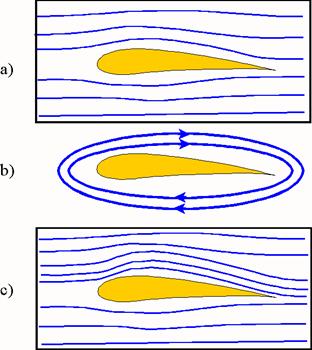
większe ciśnienie pod skrzydłem powoduje pojawienie się głównej składowej siły nośnej skrzydła nawet w locie poziomym, jak to pokazano na rysunku poniżej. Ten prosty mechanizm musi być jednak uzupełniony. Okazuje się, że partie powietrza rozdzielone przez krawędź natarcia skrzydła nie spotykają się razem na krawędzi spływu skrzydła. W rzeczywistości górna warstwa powietrza porusza się o wiele szybciej od dolnej tak, że dociera do krawędzi spływu jako pierwsza, co symbolicznie pokazano na rysunku. Eksperymentalnie stwierdzono, że prędkość w górnej warstwie powietrza może być nawet dwa razy większa od prędkości powietrza pod skrzydłem.

Ten rzeczywisty opływ skrzydła odbywa się tak jak gdyby do idealnego opływu Bernoulli’ego a) został dodany pewien modelowy ruch wirowy powietrza wokół skrzydła b). Ta modelowa cyrkulacja powietrza odbywa się zgodnie z ruchem wskazówek zegara powodując, że rzeczywisty ruch powietrza przy dolnej powierzchni skrzydła jest przez ruch wirowy wyhamowywany a przy górnej powierzchni zostaje dodatkowo przyśpieszany c). W rezultacie powstaje siła nośna większa od tej, którą przewiduje prawo Bernoulli’ego.

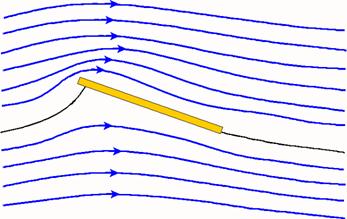
b. Ustawienie różnego od zera kąta natarcia skrzydła lub powierzchni latawca. Siła nośna powstaje także na skrzydle, nawet z symetrycznym profilem, lub na płaskiej powierzchni latawca albo deski, kiedy zostaną one ustawione pod pewnym kątem do kierunku ruchu. Ten kąt nosi nazwę kąta natarcia. Kiedy teraz skrzydło lub latawiec są ciągnięte w powietrzu (lub w wodzie) wtedy warstwa płynu zostaje przez nie odrzucana w dół. Zgodnie z III. zasadą dynamiki Newtona, takie przekazywanie powietrzu pędu skierowanego ku dołowi powoduje, że odpowiedni pęd, ale skierowany do góry, jest przekazywany także skrzydłu. Powoduje to także powstawanie na skrzydle siły nośnej. Dzięki występowaniu tej siły nośnej możliwe jest m.in. wykonywanie przez samolot lotu plecowego (odwróconego).

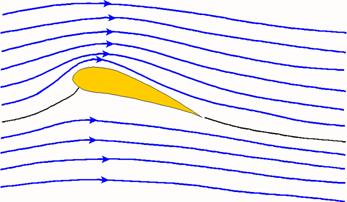
Badania eksperymentalne i symulacje komputerowe dowodzą, że kąt natarcia nie może przekroczyć 15º. Powyżej tej wartości pojawiają się silne turbulencje powietrza, przy których skrzydło jest mocno hamowane i jednocześnie traci siłę nośną. Nadmierne zwiększenie kąta natarcia nosi nazwę przeciągnięcia, przy którym samolot wchodzi w lot opadający na nos lub zwala się na skrzydło. Ponieważ jednocześnie spada skuteczność sterów to stan przeciągnięcia może prowadzić do katastrofy.

W rzeczywistości oba wymienione mechanizmy, działanie prawa Bernoulli’ego przy wyprofilowanym skrzydle oraz przekaz pędu przy większym od zera kącie natarcia, działają jednocześnie i mogą się wzajemnie wspomagać lub osłabiać. Siła nośna samolotu zależy od bardzo wielu czynników, w tym nie tylko od profilu skrzydła, ale i od jego kształtu (obrysu), od systemów redukujących turbulencje w różnej skali, od siły nośnej kadłuba itd. Poprawną ocenę siły nośnej dają tylko eksperymenty w tunelach aerodynamicznych wspomagane często symulacjami komputerowymi.

Kilka przykładów stosowanych profili skrzydeł samolotów. Aby zwiększyć siłę nośną przy małych prędkościach przy starcie i lądowaniu stosuje się w skrzydłach całe systemy klap

Back to Index