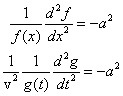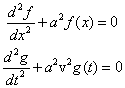Back to Index

RUCH FALOWY

Równanie różniczkowe. Prędkość fali. Amplituda i długość fali. Refrakcja.

* Ruch falowy

* Równanie różniczkowe dla ruchu falowego

* Odtworzenie równania falowego na podstawie jego rozwiazania

* Wyprowadzenie równania falowego

* Rozwiazanie równania ruchu falowego

* Parametry opisujące falę

* Prędkość ruchu falowego

* Załamanie fal

* Deformacje sprężyste

Jeżeli pewien obszar ośrodka sprężystego pobudzimy do drgań, to takie drganie zostanie przekazane innym cząstkom tego ośrodka i wtedy ruch drgający zaczyna rozprzestrzeniać się w postaci fali. Fale sprężyste mogą rozchodzić się tylko w ośrodkach materialnych wykazujących odpowiedni rodzaj sprężystości (np. kształtu, objętości), aby w tym ośrodku mogły pojawić się siły zwrotne przeciwne do kierunku deformacji. Jednocześnie ośrodki te muszą mieć niezerową gęstość konieczną do powstania sił bezwładności. Nie może, zatem, takim ośrodkiem być ani próżnia ani ciasto. Fale sprężyste różnią się zasadniczo od fal elektromagnetycznych, omawianych w części poświęconej elektrodynamice, które bez trudu rozchodzą się w próżni, ale także w każdym ośrodku materialnym, kiedy nie są w nim silnie pochłaniane.

Fale możemy podzielić ze względu na kształt frontu falowego. Jeżeli czoło fali ma kształt sferyczny, to falę nazywamy falą kulistą, a kiedy czoło fali ma kształt płaszczyzny, to falę nazywamy falą płaską. Rzeczywiste fale z reguły odbiegają od tych idealnych kształtów i ich czoła (fronty falowe) mogą mieć złożone kształty.

Jeżeli drgania, rozchodzące się w postaci fali, odbywają się w kierunku prostopadłym do kierunku ruchu fali, to falę nazywamy falą poprzeczną.

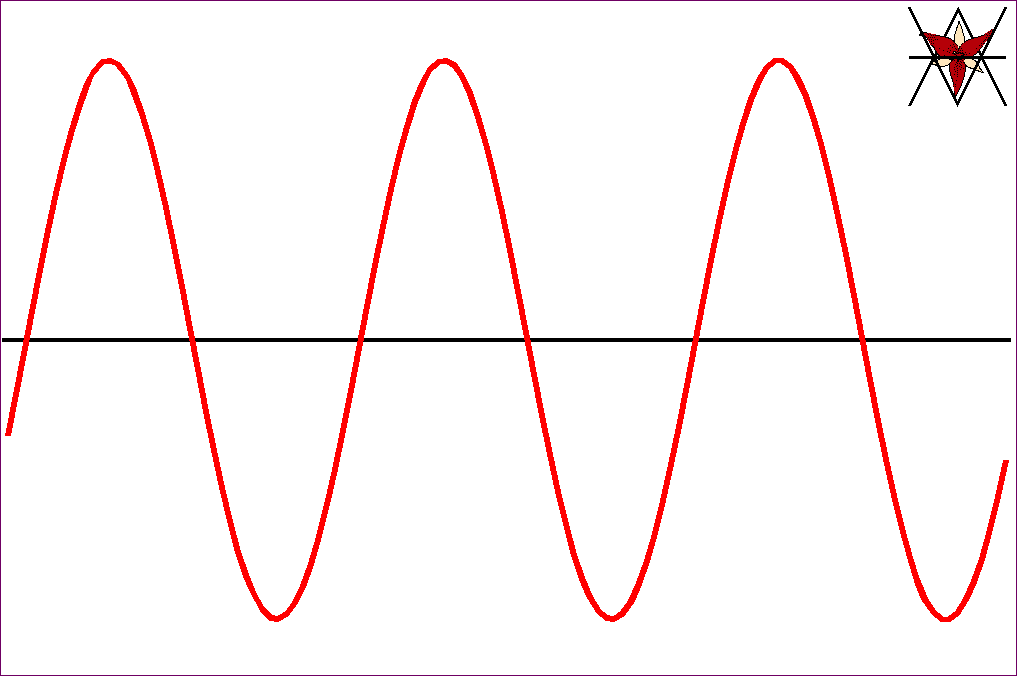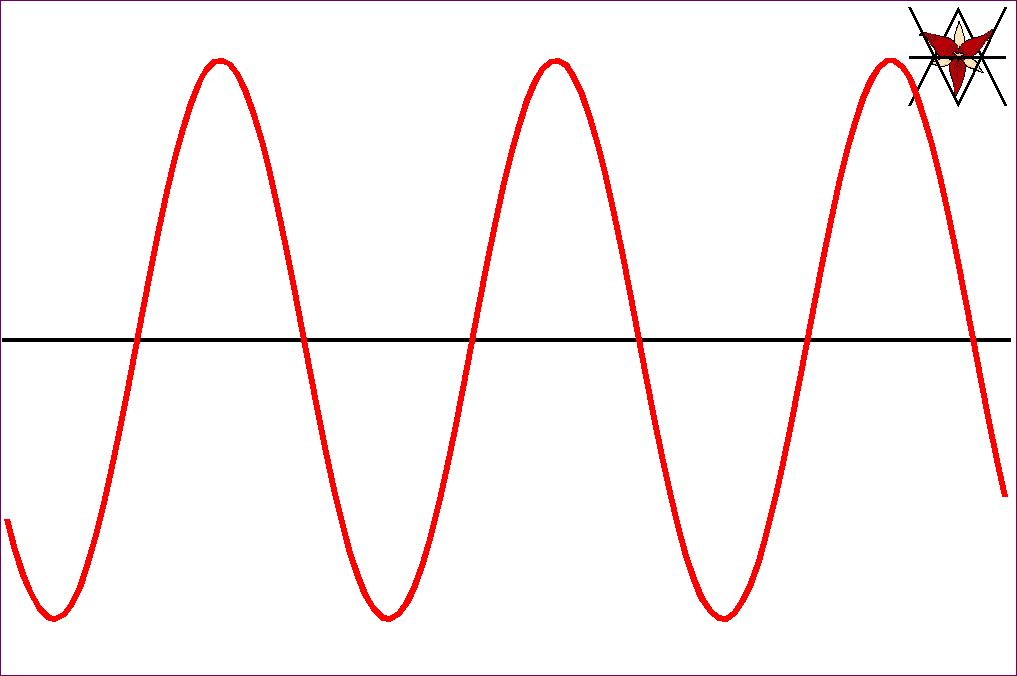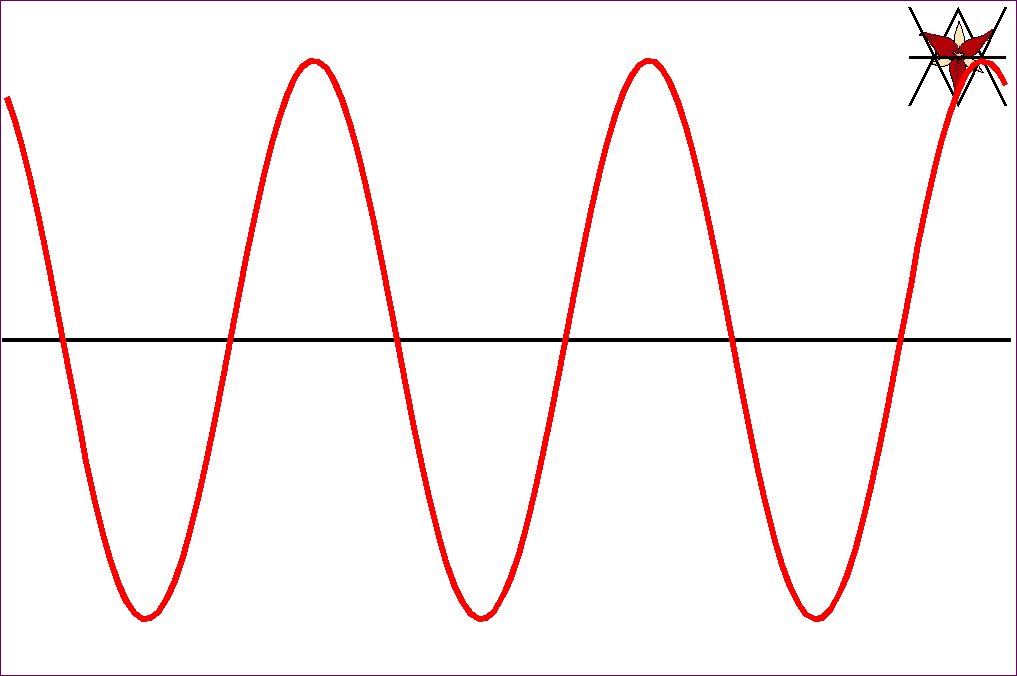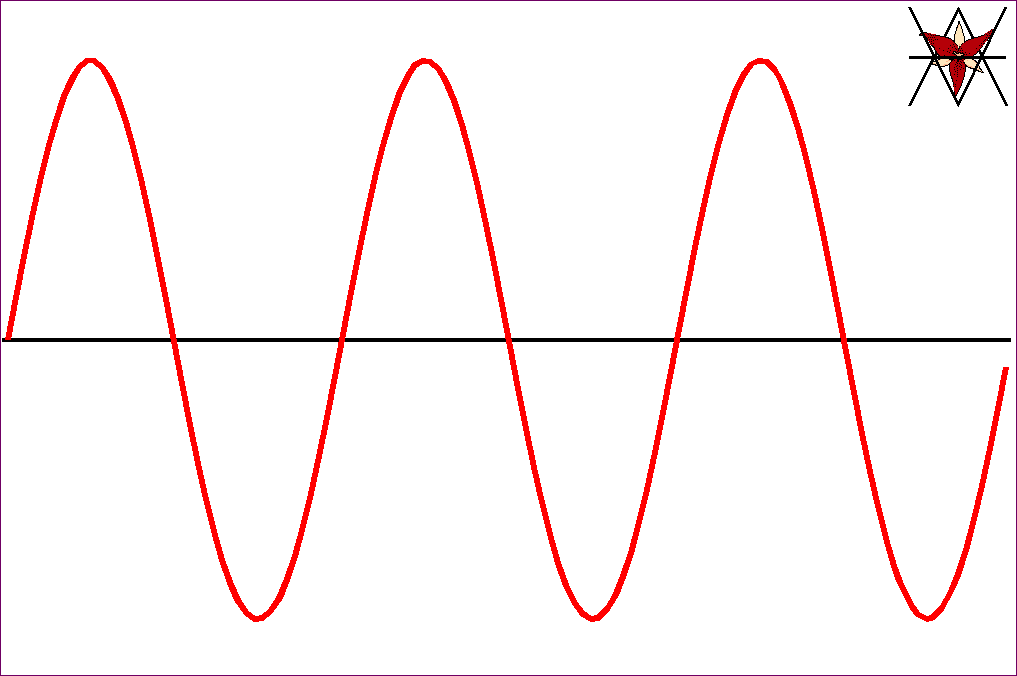
Jeżeli te drgania odbywają się w kierunku równoległym do kierunku ruchu fali (wzdłuż ruchu fali), to falę nazywamy falą podłużną.

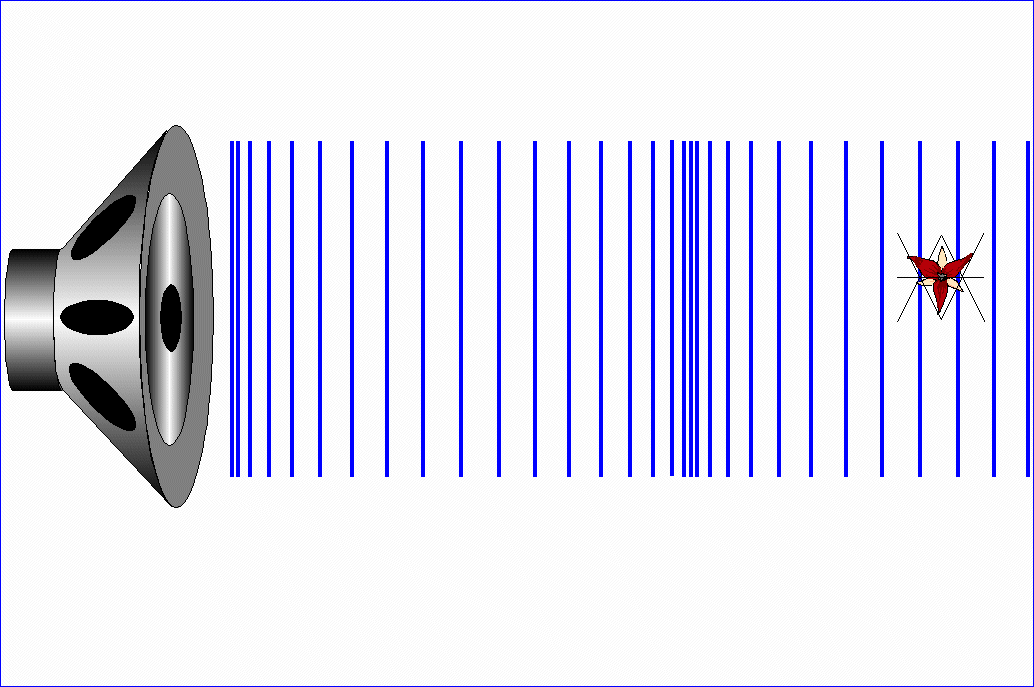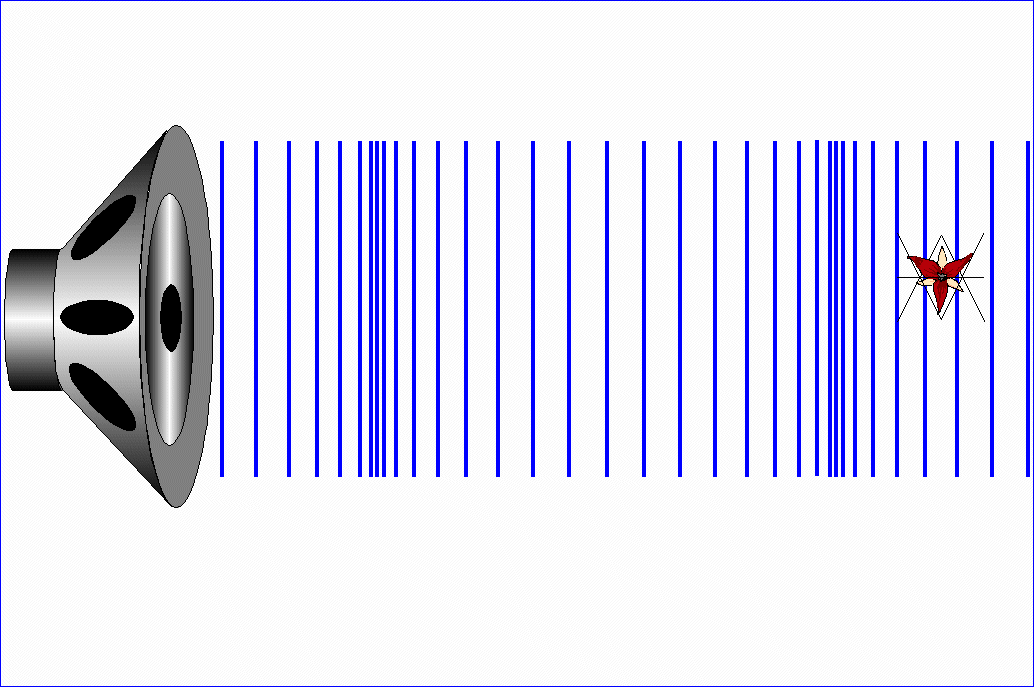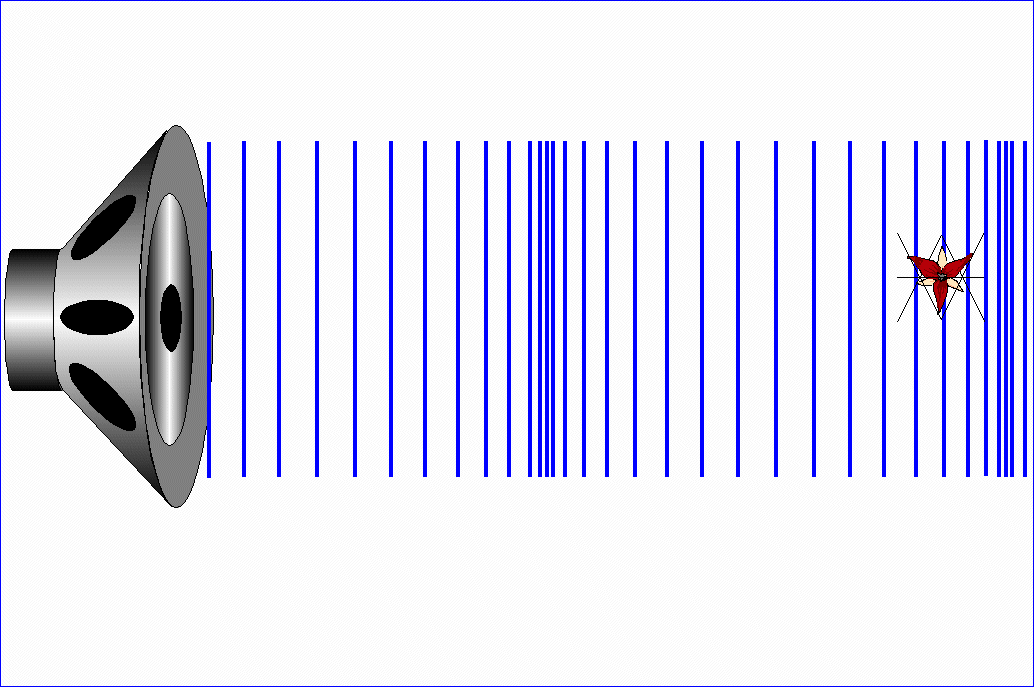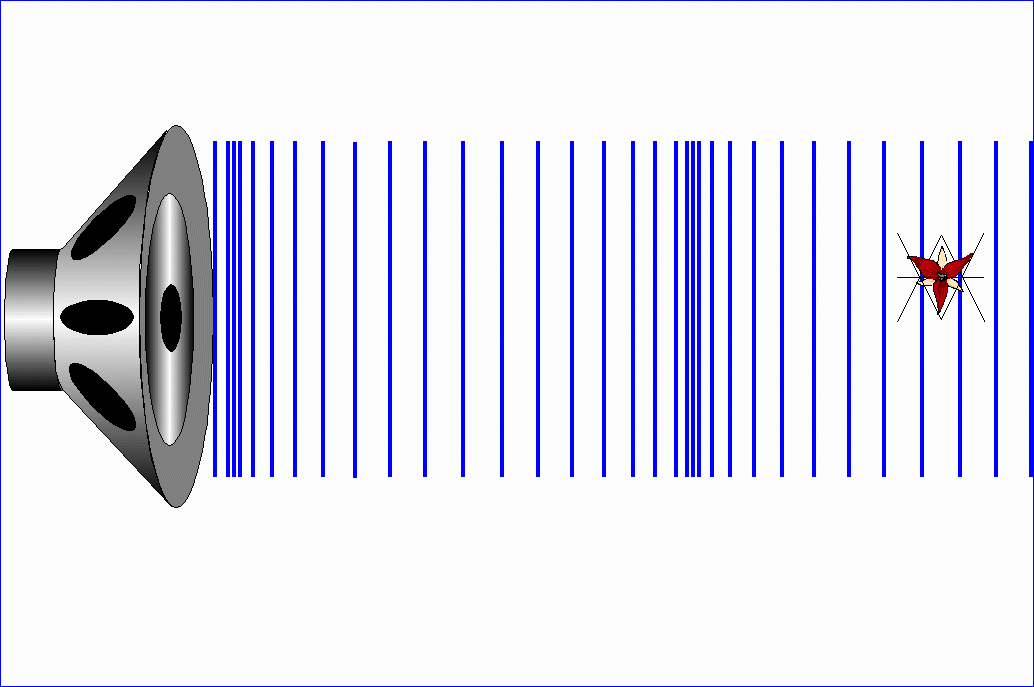
W ośrodkach, które mają sprężystość postaci (np. stal), mogą rozchodzić się fale poprzeczne i fale podłużne. W ośrodkach, które mają tylko sprężystość objętości (np. gaz), mogą rozchodzić się tylko fale podłużne.

Powierzchnia cieczy (np. wody) zachowuje sprężystość postaci i fale powierzchniowe są falami poprzecznymi. W głębi cieczy występuje tylko sprężystość objętości i tam mogą rozchodzić się wyłącznie fale podłużne.

Równanie różniczkowe, opisujące wychylenie w ruchu falowym, jest oparte na pochodnych cząstkowych drugiego rzędu tego wychylenia względem czasu i względem położenia. Dla fali rozchodzącej się w kierunku x ma ono następującą postać:

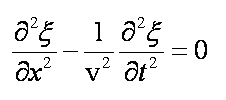
Zmienna zależna ξ jest tą wielkością, która podlega ruchowi falowemu, czyli może to być wychylenie powierzchni wody dla fali na wodzie, ale też może być lokalnym ciśnieniem w fali dźwiękowej lub wartością temperatury w fali termicznej. W powyższym równaniu zmienna ξ jest funkcją położenia x i czasu t, ξ = ξ(x, t).

Analogicznym równaniem dla fali rozchodzącej się w przestrzeni trójwymiarowej x, y, z jest:

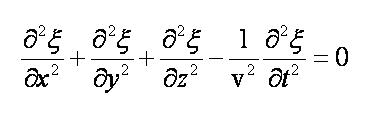
To równanie można zapisać w najbardziej zwartej postaci jako:

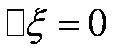
gdzie □ jest operatorem d’Alemberta (tzw. dalambercjan)

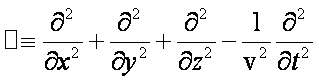
Kiedy długość fali oznaczymy symbolem λ a T będzie okresem drgań to rozwiązaniami tego równania różniczkowego dla przypadku jednowymiarowego (gdy fala rozchodzi się równolegle do osi, którą oznaczymy przez x), będą dwie funkcje x(x, t):

Dla fali rozchodzącej się w kierunku dodatnim osi x

Dla fali rozchodzącej się w kierunku ujemnym osi x

Wygodną wielkością do zapisu ruchu falowego jest wektor falowy (zwany także stałą propagacji) k = 2π/λ. Częstotliwość kątowa ω wyrażona przez wektor falowy k wynosi ω = vk. Teraz wychylenie ξ(x, t) można zapisać jako:

Dla fali rozchodzącej się w kierunku dodatnim osi x

Dla fali rozchodzącej się w kierunku ujemnym osi x

Mając wychylenie ξ(x, t) zapisane jako funkcja czasu i położenia możemy odtworzyć równanie różniczkowe, którego rozwiązaniem jest ta funkcja. W tym celu różniczkujemy dwukrotnie te funkcję i otrzymujemy

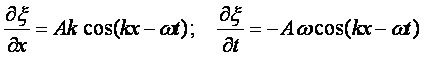
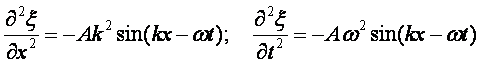
Eliminujemy sin (kx-ωt) z drugich pochodnych i znajdujemy

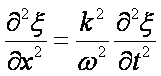
Zastosujemy przekształcenie

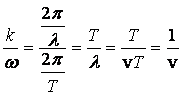
i od razu otrzymamy szukane równanie różniczkowe ruchu falowego

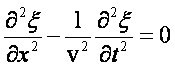
Nie możemy ograniczyć się do eliminowania funkcji trygonometrycznych już z pierwszych pochodnych, bo otrzymalibyśmy równanie pierwszego rzędu, które opisywałoby rozchodzenie się fali tylko w jednym kierunku. Dla drugiego kierunku byłoby słuszne tylko wtedy, gdy v = - v, czyli dla braku ruchu falowego.

Dla dociekliwych: Wyprowadzenie równania falowego

Już wiemy, że drgania punktu są opisywane przez równanie różniczkowe drgań

Tutaj przyjęliśmy, że drgania odbywają się w jakimś kierunku u. Ponieważ , to nasze równanie możemy zapisać w postaci równoważnej jako

Jego rozwiązaniem jest, oczywiście, i opisuje ono tylko zmiany wychylenia u w czasie, bez zmiany położenia środka drgań. T możemy nazwać czasowym okresem zmian wychylenia u.

Teraz spójrzmy na pofałdowaną, ale nieruchomą powierzchnię, np. arkusz blachy falistej. Zmiany odchylenia powierzchni u odbywają się także sinusoidalnie, ale tylko przestrzennie i są stałe w czasie. Opisując takie pofałdowanie powierzchni użyjemy równania analogicznego, jak dla drgań, ale teraz pochodną musimy wziąć po kierunku zmian, czyli względem x:

Okresem zmian przestrzennych jest tutaj długość fali λ. Rozwiązanie tego równania jest zupełnie analogiczne do poprzedniego:

.

Ponieważ w ruchu falowym zmiany odbywają się i w czasie i w przestrzeni, to połączymy oba równania różniczkowe przez wyeliminowanie u. Otrzymamy

Ponieważ , a funkcja u = u(x, t) jest teraz zależna od zmiennej przestrzennej x i od czasu t, to pochodne zwyczajne musimy zamienić na cząstkowe i w rezultacie otrzymujemy równanie falowe:

Rozwiązaniem tego równania jest, jak i poprzednio,

Dla dociekliwych: Rozwiązanie równania ruchu falowego

Rozwiązanie równania falowego możemy sprowadzić do postępowania analogicznego, jakie spotkaliśmy w równaniach drgań swobodnych. Wykorzystamy w tym celu metodę rozdzielenia zmiennych, znanej jako metoda Fouriera. Rozwiązania równania falowego

(1)

będziemy poszukiwali w postaci iloczynu dwóch funkcji f i g:

z których f(x) zależy tylko od odległości x, a g(t) zależy tylko od czasu t. Po z różniczkowaniu funkcji ξ(x, t) = f(x) g(t) dwukrotnie: najpierw względem x, a następnie względem t, otrzymamy:

Po podstawieniu otrzymanych wyrażeń do równania falowego, mamy

Równanie to przekształcimy do postaci

Ponieważ teraz lewa strona równania nie zależy od czasu, a prawa nie zależy od odległości, to obie strony muszą przyjmować jednakową stałą wartość. Tę wartość nazwiemy stałą separacji i dla wygody oznaczymy przez -a². Po takim zabiegu, równanie falowe zostanie rozdzielone na dwa niezależne równania:

czyli

(2)

Otrzymane równania różniczkowe o pochodnych zwyczajnych (2) mają postać analogiczną do równań drgań swobodnych. Ich rozwiązaniami będą funkcje f(x) i g(t) o znanej nam postaci typu cosωt. Teraz argumentami funkcji cos będą odpowiednio ax oraz avt, czyli:

Zatem rozwiązanie szczególne dla ξ = f(x)@g(t) otrzymamy w postaci

Aby przekształcić to wyrażenie, korzystamy z równości trygonometrycznej

i znajdujemy, że

Teraz pozostaje jeszcze wyznaczyć stałą a. Jej wartość otrzymamy wykorzystując fakt, że przesunięcie fali o odległość równą długości fali λ nie zmienia jej obrazu, czyli jest równoważne zwiększeniu (lub zmniejszeniu) argumentu funkcji cos o 2π. Możemy więc napisać

Stąd wynika, że a = 2π/λ. Rozwiązanie przybiera więc postać

Ponieważ v/λ = 1/T, to powyższe rozwiązanie zapiszemy jako

albo

gdzie k = 2π/λ jest liczbą falową, a ω = 2π/T = 2πf jest częstotliwością kątową drgań fali. Otrzymane rozwiązanie jest sumą dwóch fal typu

gdzie A jest amplitudą fali. Pierwsza z nich jest falą rozchodzącą się w kierunku ujemnym osi x, a druga falą, która biegnie w kierunku dodatnim tej osi. Mamy zatem dwa rozwiązania równania falowego (1):

dla fali biegnącej w kierunku wyznaczonym przez kierunek osi x

oraz dla fali biegnącej w kierunku przeciwnym

Łatwo sprawdzić, że każde z tych rozwiązań spełnia równanie falowe (1).

Tradycyjnie ruch falowy przedstawiamy w postaci poprzecznej płaskiej fali sinusoidalnej. Maksymalne wychylenie liczone od położenia zerowego (równowagi) nazywamy amplitudą fali A. Długość fali λ możemy przedstawić jako odległość między sąsiednimi „garbami” lub, bardziej ogólnie, między najbliższymi położeniami o tej samej fazie ruchu.

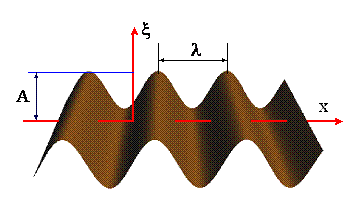
Tutaj, jak i poprzednio, fala rozchodzi się w kierunku x, a wychylenie oznaczamy literą ξ. Falę podłużną możemy przedstawić jako kolejne zagęszczenia i rozrzedzenia ośrodka przebiegające wzdłuż kierunku rozchodzenia się fali

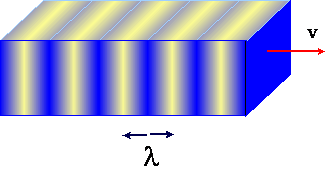
Długość fali podłużnej λ określamy analogicznie, jak poprzednio. Jeżeli prędkość rozchodzenia się fali jest v, a okres pełnego cyklu fali wynosi T, to długość fali l jest związana z v i T oczywistą zależnością

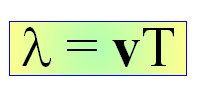
Ważne jest, aby zauważyć, że wyrażenie matematyczne, które opisuje wychylenie w ruchu falowym , różni się istotnie od znanego już nam równania opisującego wychylenie w zlokalizowanym ruchu drgającym . Wyrażenie opisujące ruch falowy musi uwzględniać zależności tak do czasu, jak i od położenia wzdłuż kierunku rozchodzenia się fali.

Prędkość rozchodzenia się fali zależy od jej typu i od rodzaju ośrodka, w której się rozchodzi. Wyrażenie opisujące prędkość ruchu falowego zawiera dwa czynniki: czynnik sprężystości i czynnik bezwładności:

Prędkość fal poprzecznych (w ciałach stałych)

gdzie G - moduł sprężystości postaci (moduł sztywności), zaś ρ -gęstość. Dla struny wzór ten można przedstawić w postaci

gdzie F_t - naprężenie struny, μ - gęstość liniowa (masa na jednostkę długości).

Prędkość fal podłużnych

W ciałach stałych

E - moduł Younga.

W cieczach

B - moduł ściśliwości (bulk modulus).

W gazach

gdzie κ = c_p/c_v, zaś p - ciśnienie.

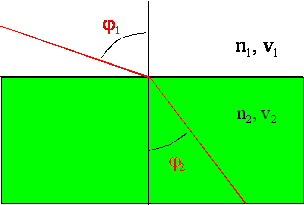
Załamywanie się fal na granicy dwóch ośrodków jest wywołane przez różnicę prędkości fali w tych ośrodkach. Współczynnik załamania n jest określony przez stosunek prędkości rozchodzenia się fal w obu ośrodkach

Przy przechodzeniu fali z próżni (powietrza) do ośrodka, w którym fala (światło) ma prędkość v współczynnik załamania n wynosi

Przy przechodzeniu światła kolejno przez kilka ośrodków, wzór Snelliusa wygodnie napisać w postaci:

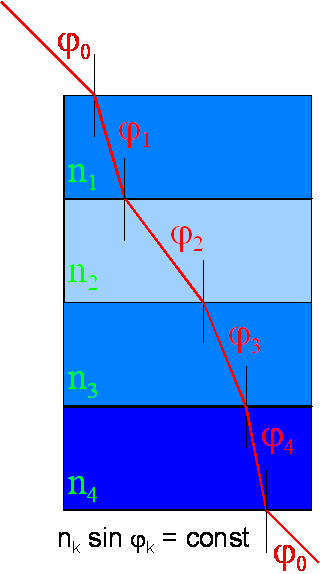
Wartość stałej ‘const’ jest określona przez pierwszy kąt padania φ₀.

Zawsze, kiedy na ciało działają siły, zewnętrzne czy wewnętrzne, wtedy ciało ulega deformacjom. Gdy po ustaniu działania sił ciało powraca do swojej postaci pierwotnej wtedy mówimy, że ciało było poddane deformacji sprężystej. Kiedy jednak ciało nie może już samo wrócić do stanu pierwotnego to oznacza, że w trakcie deformacji została przekroczona granica sprężystości i odkształcenie ma charakter plastyczny co oznacza, że w trakcie deformacji nastąpiła przebudowa struktury wewnętrznej ciała. Deformacje sprężyste występują tak w przypadku jednorazowo przyłożonej siły (aperiodycznej) jak i w ruchu falowym, kiedy to siły działają okresowo (periodycznie).

W opisie deformacji sprężystych bierzemy pod uwagę dwie zasadnicze wielkości: NAPRĘŻENIE (stress) i wywołane przez nie ODKSZTAŁCENIE (strain).

Wyróżniamy trzy typy naprężeń:

rozciąganie (ściskanie)

wszechstronne ściskanie

ścinanie (skręcanie)

Prawo Hooke’a: (Ut tensio sic vis - takie wydłużenie, jaka siła). Prawo Hooke’a opisuje najprostszą deformację rozciąganego (ściskanego) pręta, którego wydłużenie Δl jest wprost proporcjonalne do przyłożonej siły F:

Na podstawie danych eksperymentalnych znajdujemy

gdzie A jest powierzchnią przekroju poprzecznego zaś E jest znany jako moduł sprężystości albo jako moduł Younga.

Naprężenie = Siła/Powierzchnia = F/A

Wydłużenie względne = Zmiana długości/Długość początkowa = Δl/l₀

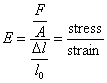
Analogiczne wyrażenia możemy otrzymać dla ścinania i wszechstronnego ściskania. Dla ścinania

albo

ponieważ dla małych odkształceń )l/l₀ = sinM = tgM = M. Stała G nosi nazwę modułu sztywności. Z reguły jest on równy od 1/2 do 1/3 wartości modułu Younga E.

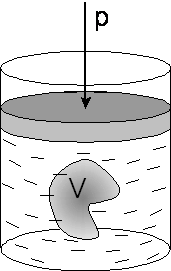
Jeżeli ciało jest poddane jednorodnemu ściskaniu, to zmniejszenie jego objętości )V wyniesie

gdzie stała B nosi nazwę modułu ściśliwości (sprężystości objętościowej) (od “bulk”).

Wymiary ciała D w kierunku poprzecznym do kierunku naprężenia ulegają zmniejszeniu

współczynnik σ nosi nazwę współczynnika Poissona. Istnieją zatem cztery stałe opisujące własności sprężyste ciał stałych: E, G, B i σ. Tylko trzy z nich są niezależne, ponieważ istnieją związki między nimi:

Energia potencjalna związana z deformacją sprężystą.

Praca elementarna deformacji wynosi

ale

czyli

stąd

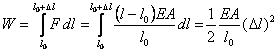
Ponieważ objętość ciała przed deformacją V = A l₀, to

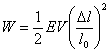
Oznaczając Δl/l₀ = ε, gęstość energii deformacji w = W/V otrzymujemy w postaci

Jest to wyrażenie przybliżone, ponieważ objętość V została wzięta dla ciała przed deformacją. Podobne wyrażenia możemy otrzymać także dla pozostałych typów deformacji.

Back to Index