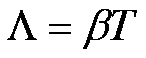DYNAMIKA

DRGANIA TŁUMIONE

Równanie różniczkowe drgań tłumionych. Logarytmiczny dekrement tłumienia.

Stosunkowo prostym przypadkiem drgań tłumionych są takie drgania, w których siła tłumiąca ruch jest wprost proporcjonalna do prędkości ruchu v ciała drgającego.

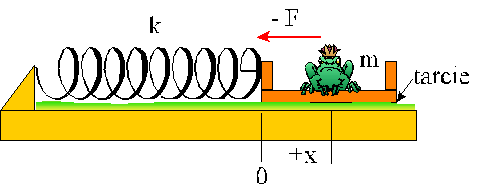
Wtedy do siły zwrotnej sprężyny –kx zostaje dodana siła tarcia –bv zawsze przeciwnie skierowana do kierunku ruchu. Teraz sumaryczna siła działająca na ciało drgające wzdłuż osi x wynosi F_x = - kx - bv a równanie ruchu otrzymuje się z drugiej zasady dynamiki Newtona:

Podstawiamy: b/m = 2β (β - współczynnik tłumienia) oraz k/m = ω₀² i równanie przybiera postać:

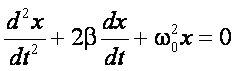
stosując podstawienie x = e^λt otrzymujemy równanie charakterystyczne

Pierwiastkami tego równania są

Jeżeli β <ω₀, wtedy wprowadzamy oznaczenie β² - ω₀² = (iω)², gdzie

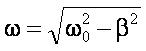
Tak więc

Rozwiązanie ogólne równania początkowego jest więc

Człon w nawiasach kwadratowych [ ] jest zupełnie analogiczny do otrzymanego dla prostych drgań harmonicznych i może być przepisany jako

W rezultacie otrzymujemy rozwiązanie końcowe w postaci

Zanik amplitudy drgań tłumionych dla wybranych parametrów ω i β jest przedstawiony na rysunku poniżej.

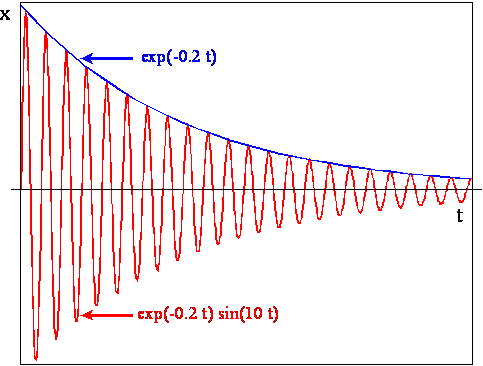
Na podstawie wartości współczynnika tłumienia β w relacji do częstotliwości kołowej drgań nietłumionych ω₀ stopień tłumienia można zgrubnie podzielić na:

Tłumienie podkrytyczne: β < ω₀. Zwykłe drgania tłumione.

Tłumienie krytyczne: β = ω₀. W tym przypadku układ dochodzi najszybciej do stanu równowagi.

Tłumienie nadkrytyczne: β > ω₀. Pierwiastki równania charakterystycznego są teraz rzeczywiste i drgania są zerwane (występuje „pełzający” powrót do stanu równowagi).

Logarytmiczny dekrement tłumienia charakteryzuje efektywność tłumienia i jest definiowany jako logarytm naturalny ze stosunku dwóch wychyleń x, jednego wziętego w momencie t a drugiego wziętego w momencie późniejszym o jeden okres drgań T, czyli t + T.

Zatem logarytmiczny dekrement tłumienia Λ jest równy iloczynowi współczynnika tłumienia β i okresu drgań T:

Back to Index