Back to Index

SKŁADANIE DRGAŃ HARMONICZNYCH

Rozkład drgań nieharmonicznych na szeregi Fouriera. Analiza harmoniczna.

* Szeregi Fouriera

* Analiza harmoniczna

Składanie drgań równoległych ma również inne, niezwykle ważne, zastosowania w nauce i technice. Problem leży w tym, że wiele obserwowanych lub celowo generowanych drgań ma charakter bardziej złożony niż drgania harmoniczne. Drgania, których kształty nie są opisywane sinusoidą lub cosinusoidą, jak np. drgania trójkątne, piłokształtne, prostokątne itd., nie są drganiami harmonicznymi

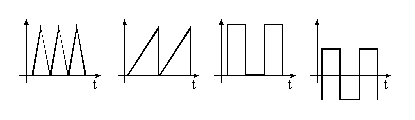
Istnieje jednak wspaniała technika, zwana analizą harmoniczną (lub analizą Fouriera), która pozwala drgania okresowe o dowolnym kształcie przedstawić jako sumę drgań harmonicznych. Technika ta polega na rozkładaniu analizowanego drgania okresowego na drgania harmoniczne, czyli na przedstawianiu okresowej funkcji czasu f(t) jako sumy nieskończonego szeregu trygonometrycznego, którego wyrazy są funkcjami albo tylko sinus lub tylko cosinus. W praktyce szereg „nieskończony” składa się z nie więcej niż z 20-30 wyrazów. Podstawowa cecha tych szeregów jest taka, że jeżeli funkcja f(t) zmienia się okresowo z okresem T, to pierwszy wyraz szeregu ma częstotliwość , zwaną częstotliwością podstawową, a następne mają częstotliwości harmoniczne, tzn. będące całkowitymi wielokrotnościami częstotliwości podstawowej, czyli 2ω, 3ω, 4ω ... Żadne z tych drgań nie może mieć częstotliwości mniejszej od ω ani częstotliwości nie będącej całkowitą wielokrotnością ω , np. nie może być 3.5 ω . Widać więc, że okres drgań T = 2π/ω odpowiadający częstotliwości podstawowej ω jest najdłuższym okresem jakie mogą mieć składowe Fouriera. Poniżej przedstawiono obraz rozkładu drgania złożonego na składowe Fouriera.

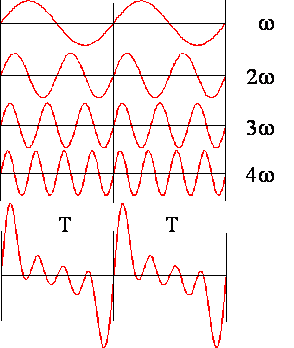
Tworzenie się drgania piłokształtnego jako sumy wyrazów szeregu Fouriera jest przedstawione w animacji poniżej:

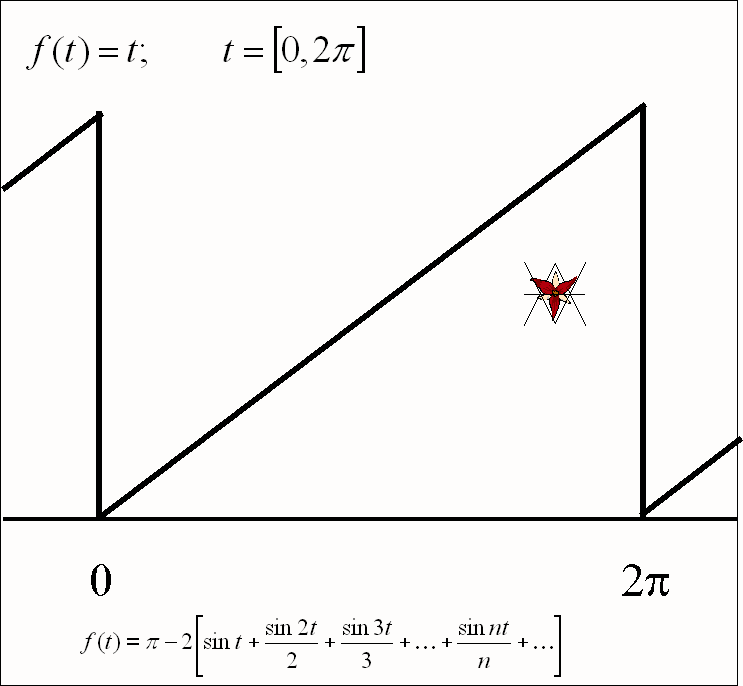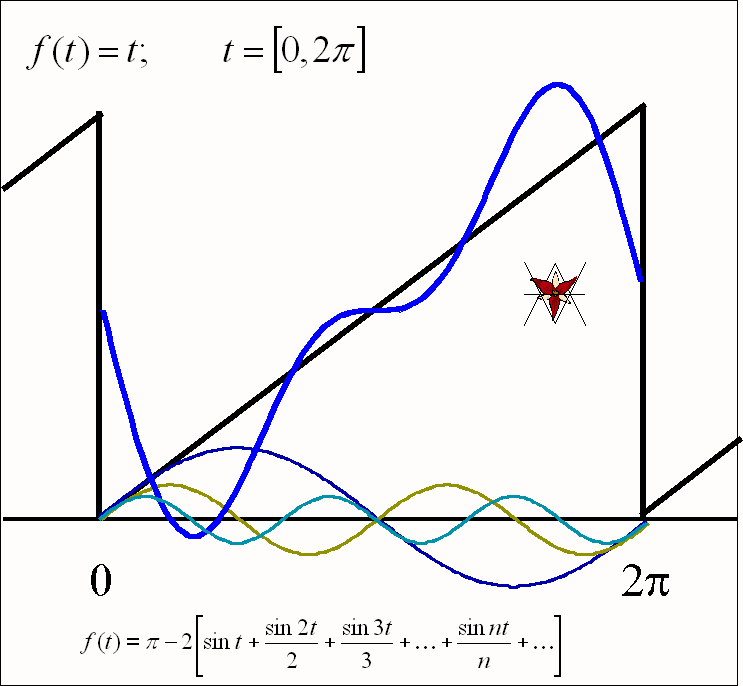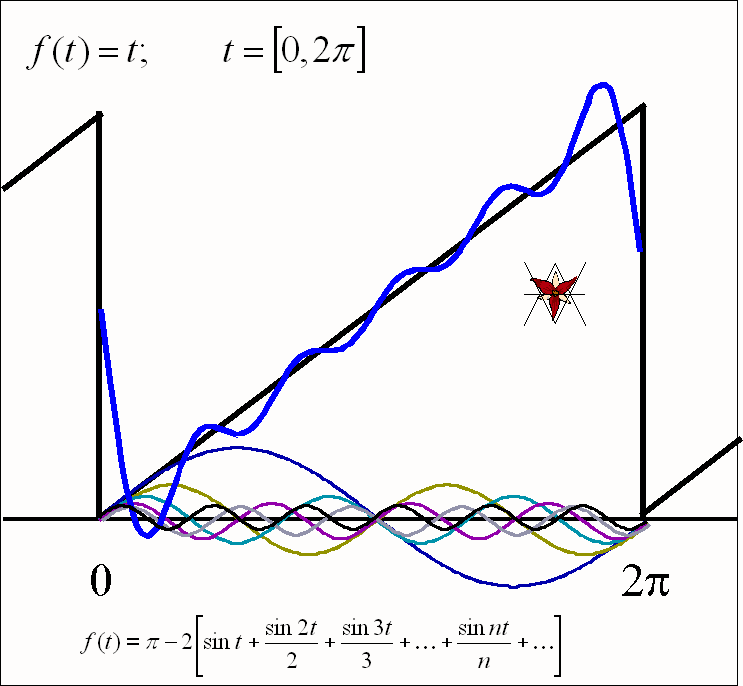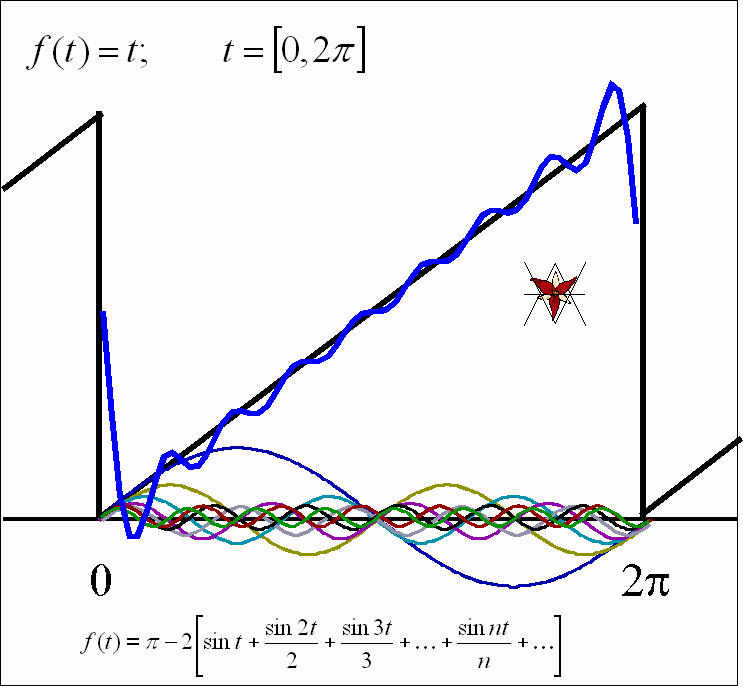
Szereg Fouriera ma następującą postać:

(1)

gdzie współczynniki a₀, a_n i b_n noszą nazwę współczynników Fouriera:

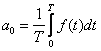
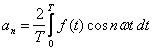
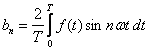
Widać zatem, że rozkład określonego drgania w szereg Fouriera sprowadza się w rzeczywistości jedynie do znalezienia współczynników Fouriera wg powyższych równań.

Równania określające współczynniki Fouriera zostały znalezione w oparciu o wspaniałą własność funkcji trygonometrycznych zwaną ortogonalnością. Mówimy, że dwie funkcje są ortogonalne względem siebie, gdy całka z ich iloczynu, wzięta po całym okresie zmienności tego iloczynu, jest równa zeru. Oznacza to, że dla całkowitych m i n jeśli m jest różne od n to są spełnione równania

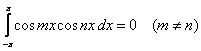
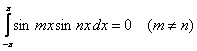
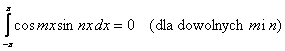
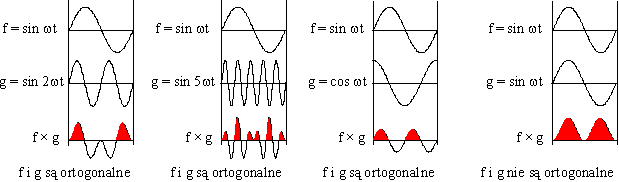
Granice całkowania mogą być inne pod warunkiem, że przedział całkowania będzie miał długość odpowiadającą okresowi 2π. Geometrycznie ortogonalność oznacza, że dla krzywej iloczynu dwóch funkcji ortogonalnych powierzchnia nad osią układu jest równa powierzchni pod osią. Na rysunku poniżej przedstawiono ortogonalność funkcji sin ωt i sin 2ωt, sin ωt i sin 5ωt oraz sin ωt i cos ωt. Funkcja sin ωt nie jest ortogonalna względem samej siebie.

Szukając n-tego współczynnika, obie strony równania (1) mnożymy przez cos(nωt) dla współczynnika a_n lub przez sin(nωt) dla współczynnika b_n. Następnie wyliczamy wartości średnie obu stron równania w całym okresie zmienności [0, T]:

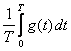
W przedziale [0, T] wartość średnia funkcji cos(nωt) i sin(nωt) jest, oczywiście, równa zeru. Iloczyny funkcji trygonometrycznych zamieniamy wg reguł:

A zatem, wartości średnie iloczynów będą następujące:

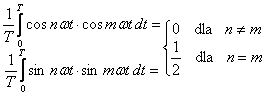
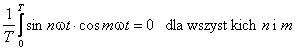
Teraz łatwo znajdujemy współczynniki a_n i b_n:

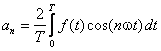
Jeżeli, na przykład, szukamy współczynnika a₄, mnożymy obie strony równania (1) przez cos4ωt i otrzymujemy

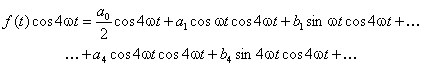
Piszemy wyrażenie na wartość średnią w przedziale [0, T] obu stron otrzymanego równania

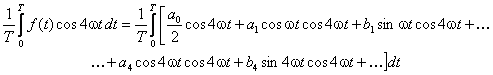
Po zastosowaniu relacji ortogonalności znajdujemy, że jedynym niezerowym wyrazem po prawej stronie będzie

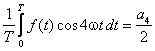
Stąd

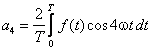
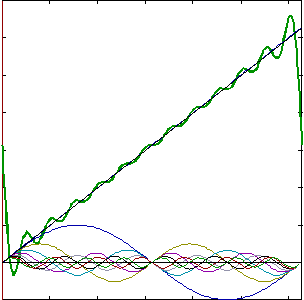
Przykłady rozwinięć w szeregi Fouriera kilku funkcji okresowych oraz graficzne zaprezentowanie wyrazów szeregu i ich sumy:

1. Drgania piłokształtne f(t) = t w przedziale [0, 2B]:

2. Drgania prostokątne 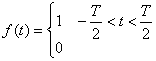o okresie T:

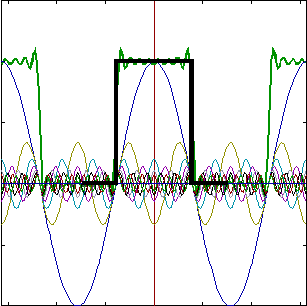
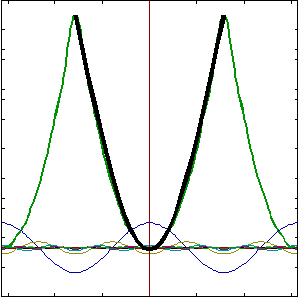
3. Drgania paraboliczne f(t) = t² w przedziale [ -π, π]:

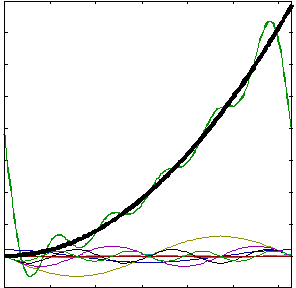
4. Parabola f(t) = t² w przedziale [0, 2π]:

5. Drgania prostokątne

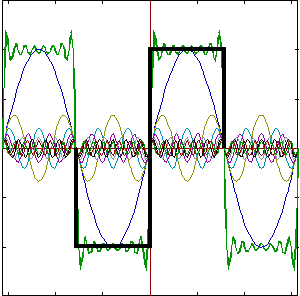
Wzór Eulera jest znakomitym narzędziem także w analizie harmonicznej, czyli w analizie zawartości drgań harmonicznych w badanym okresowym drganiu nieharmonicznym.

Jeżeli do szeregu Fouriera (1)

ze współczynnikami Fouriera

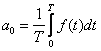
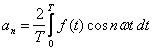
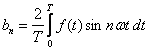
zastosujemy wzór Eulera,

wtedy funkcje trygonometryczne z szeregu (1) otrzymamy w postaci

Po podstawieniu tych wyrażeń do równania (1) otrzymujemy

oraz

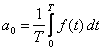
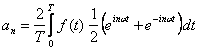
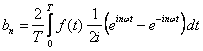
Te wyrażenia łatwo przekształcamy do postaci

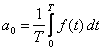
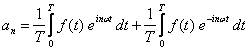
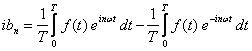
Możemy teraz zdefiniować nowe współczynniki

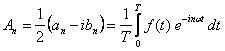
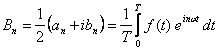
a wtedy szereg Fouriera otrzymujemy w postaci

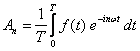
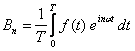
Kiedy następnie zmienimy granice sumowania z (1, ∞) na (-∞, ∞) to zniknie nam wyraz a₀ a sam szereg Fouriera będziemy mogli zapisać w postaci bardzo prostej z jednym tylko współczynnikiem c_n:

(2)

Współczynnik c_n wyraża się wzorem

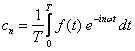
Relacja ortogonalności jest teraz także bardzo prosta:

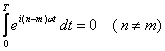
Zaletą przedstawienia szeregu Fouriera w postaci zespolonej jest możliwość scharakteryzowania drgania nieharmonicznego za pomocą jednego tylko widma. Rzeczywiście, równanie (2)

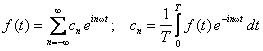
może być w prosty sposób zilustrowane przez widmo częstotliwości utworzone przez ciąg odcinków prostopadłych do osi czasu t, z których każdy obrazuje wartość i znak każdej n-tej składowej harmonicznej:

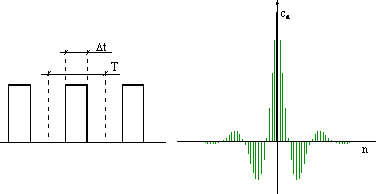
Widmo częstotliwości zmienia się w miarę zmian gęstości impulsów (stopnia wypełnienia) gdzie Δt czasem trwania impulsu a T jest okresem jego powtarzania się. Im stopień wypełnienia impulsu jest mniejszy (impulsy stają się coraz krótsze w stosunku do długości całego okresu) tym gęściej ustawione są odcinki tworzące widmo:

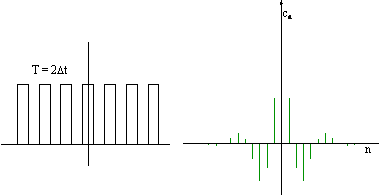
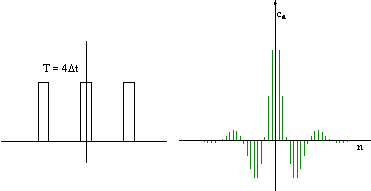
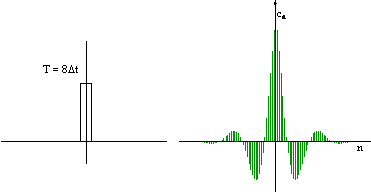
Widmo częstotliwości pozwala jednym rzutem oka ocenić zawartość harmonicznych w konkretnym analizowanym przebiegu okresowym.

Back to Index