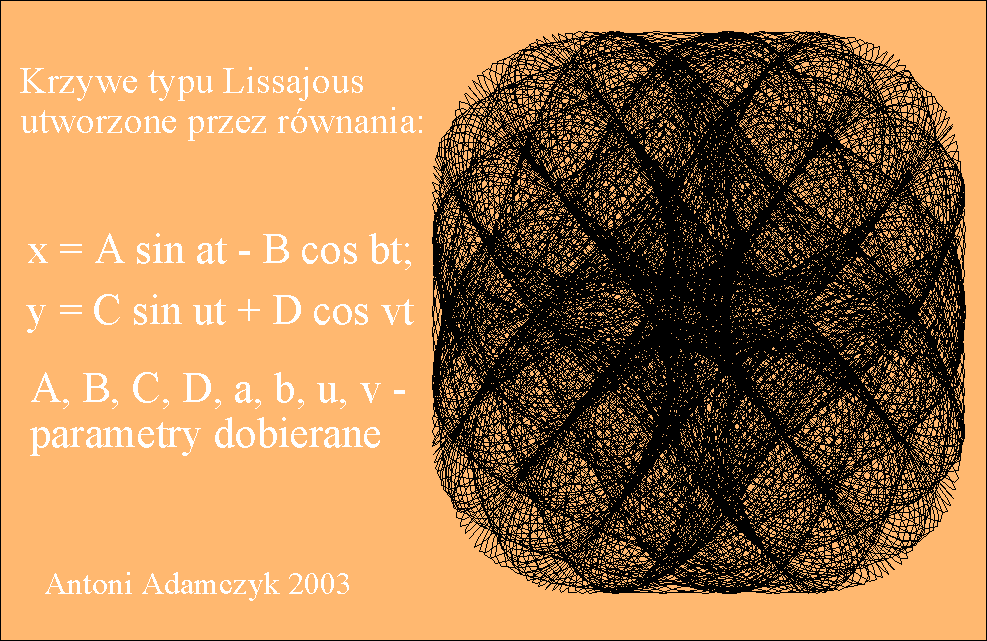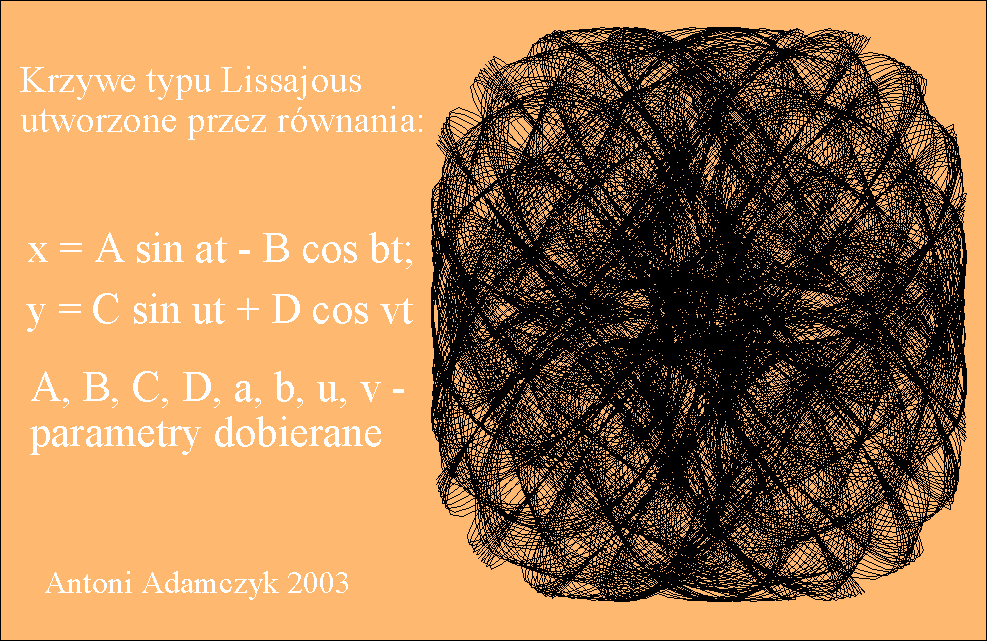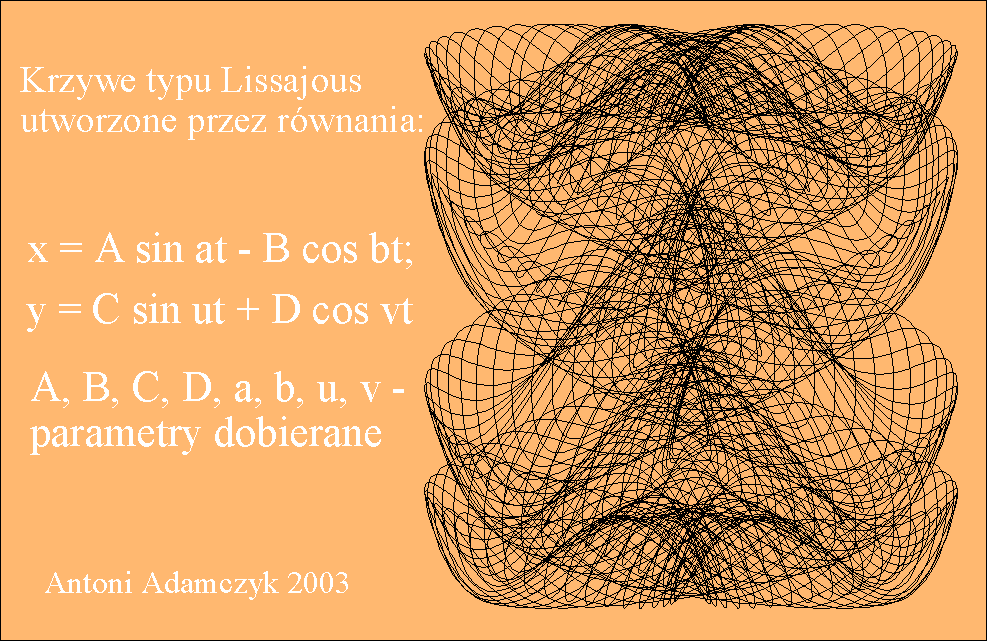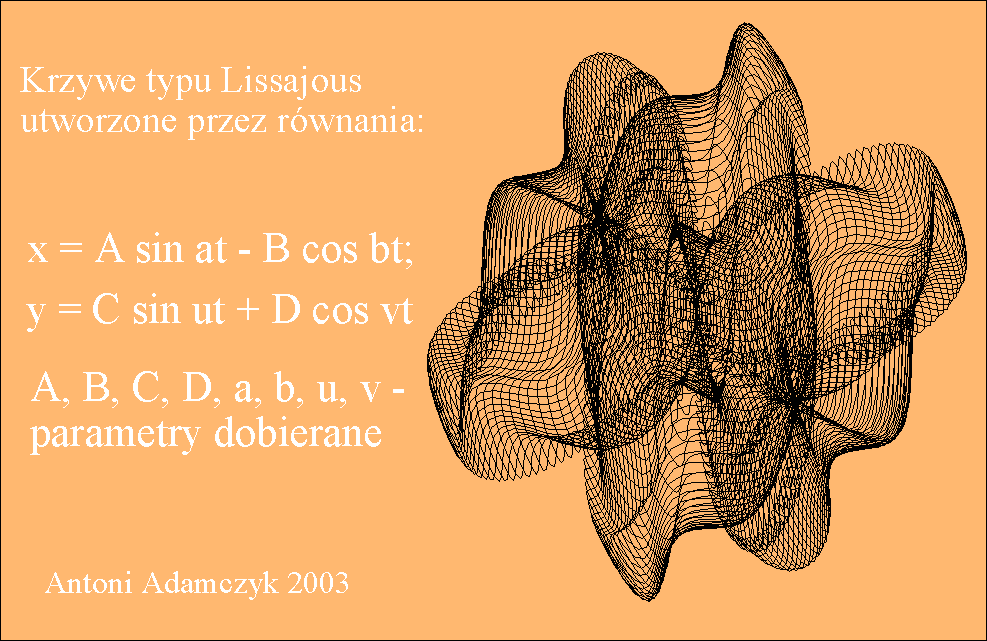Back to Index

SKŁADANIE DRGAŃ HARMONICZNYCH

Dudnienia. Krzywe Lissajous.

* Składanie drgań harmonicznych

* Składanie drgań równoległych – dudnienia

* Składanie drgań prostopadłych – krzywe Lissajous

* Składanie bardziej złożonych drgań prostopadłych

Jeżeli pewien punkt jest poddany jednoczesnemu pobudzeniu przez dwa niezależne źródła drgań (sprężyny, generatory itp.), to ten punkt będzie wykonywał drganie będące sumą obu drgań. Mówimy wtedy o składaniu drgań. Chociaż składanie drgań może dotyczyć drgań o dowolnym kształcie, to ograniczymy się do sytuacji, w których oba źródła wykonują drgania harmoniczne. Możemy wyróżnić dwa interesujące przypadki szczególne:

1. oba drgania odbywają się w tym samym kierunku i wtedy będziemy mieli składanie drgań równoległych. Występuje wtedy bardzo efektowne zjawisko zwane dudnieniem, które ma także ważne znaczenie w technice pomiarowej.

2. oba drgania odbywają się w kierunkach prostopadłych do siebie i wtedy mówimy o składaniu drgań prostopadłych. Pod działaniem drgania wypadkowego punkt porusza się po torze, który często jest bardzo skomplikowaną krzywą mającą często fantastyczne walory graficzne. Stosunkowo najmniej skomplikowane z tych krzywych noszą nazwę krzywych Lissajous.

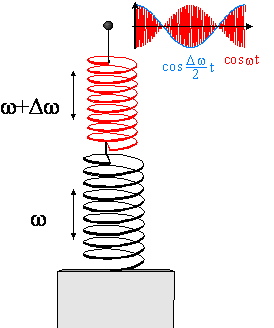
Jeżeli dwa drgania mają bardzo podobne częstotliwości kołowe, ω oraz ω+Δω, przy czym Δω << ω, a ponadto jeżeli oba te drgania odbywają się w tym samym kierunku i są opisywane równaniami

to suma tych drgań będzie wynosiła

Ponieważ wiadomo, że

to równanie drgań wypadkowych można zapisać jako

Na podstawie przyjętego warunku Δω << ω można napisać, że cos (ω+Δω/2)t ≈ cos ωt . W tym przybliżeniu otrzymujemy końcowe równanie sumy drgań:

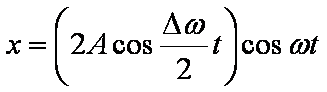
Człon w nawiasie możemy traktować jako zależną od czasu amplitudę drgań harmonicznych o częstotliwości kołowej ω. Ta zmiana amplitudy o małej częstotliwości kątowej Δω/2 jest istotą zjawiska nazywanego dudnieniem. Należy zauważyć, że amplituda drgania wypadkowego jest dwa razy większa od amplitudy drgań składowych.

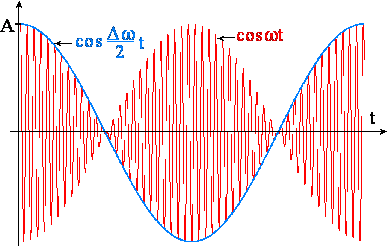
Szczególnie łatwo usłyszeć dudnienia w fali dźwiękowej. Jeżeli dwa źródła (głośniki, kamertony) emitują fale dźwiękowe o nieco różnych częstotliwościach, to do naszych uszu dochodzi dźwięk sumaryczny wynikający z nakładania się drgań równoległych (fala dźwiękowa jest falą podłużną). W animacji poniżej obie fale składowe, czerwona i zielona, powodują powstanie fali rozchodzącej się jako dudnienie (czarny wykres).

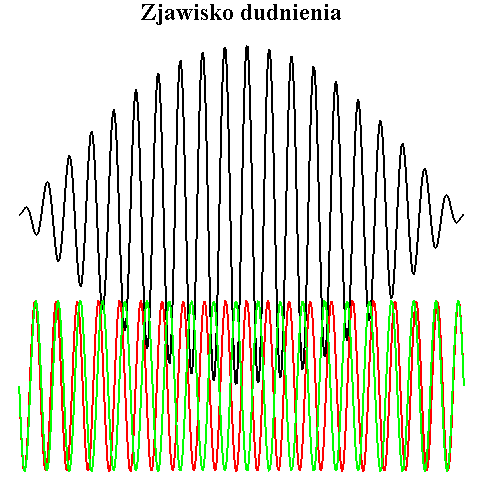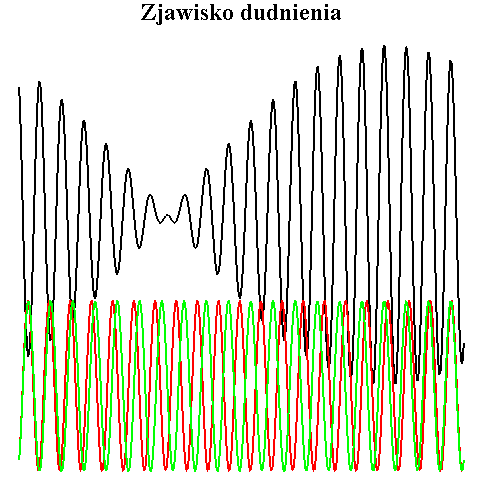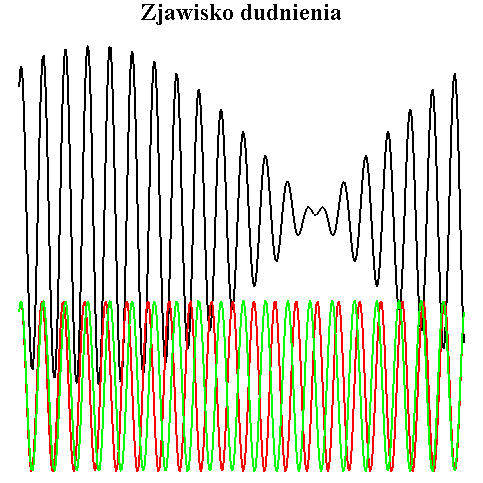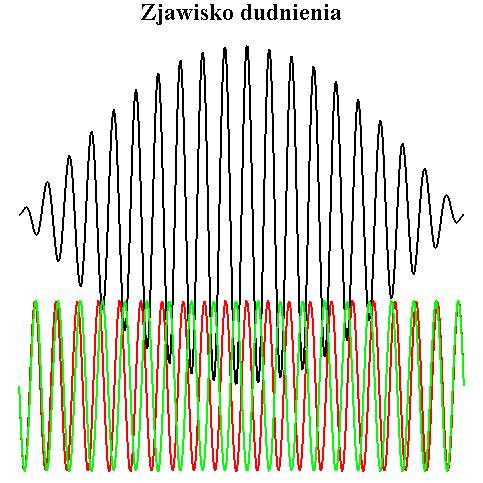
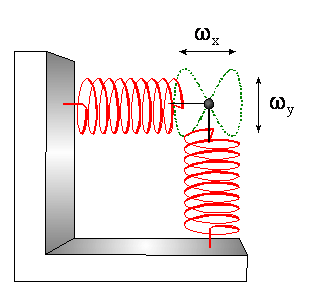
Jeżeli pewien punkt wykonuje jednocześnie dwa drgania, które odbywają się w różnych kierunkach to drganie wypadkowe (sumaryczne) może być bardzo złożone mimo, że każde z drgań składowych jest proste. Rozważmy punkt wykonujący jednocześnie dwa proste drgania harmoniczne w dwóch prostopadłych kierunkach, np. wzdłuż osi x i y:

Torem punktu będzie pewna krzywa płaska, której kształt zależy od stosunku obu częstotliwości ω_x i ω_y i od przesunięcia fazowego φ między oboma drganiami

Równanie toru, po jakim będzie poruszał się punkt otrzymujemy z równań drgań przez eliminację czasu. Jest to postępowanie analogiczne do robienia fotografii, na której czas dla fotografowanego obiektu ulega zatrzymaniu. Zagadnienie poszukiwania toru punktu można podzielić na dwa główne przypadki:

I. Obie częstotliwości kołowe są równe: ω_x = ω_y = ω

Z pierwszego równania otrzymujemy

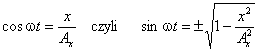
Ponieważ cos (α + β) = cosα cosβ - sinα sinβ, to stosując odpowiednie podstawienia w drugim równaniu możemy napisać

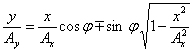
Po uporządkowaniu znajdujemy równanie toru:

Jest to równanie elipsy nachylonej pod kątem φ do osi układu odniesienia.

Przypadki szczególne elipsy:

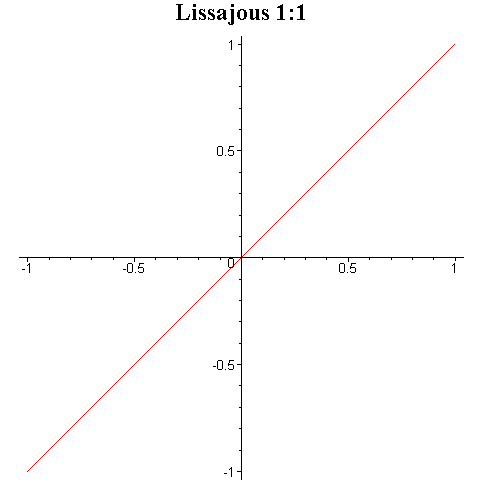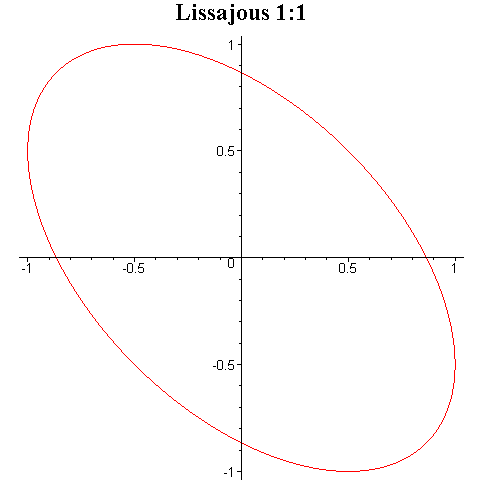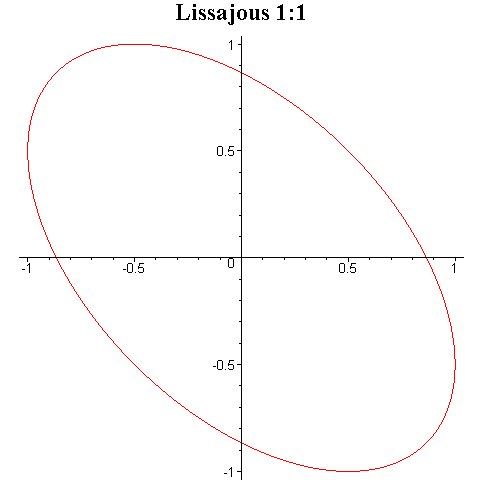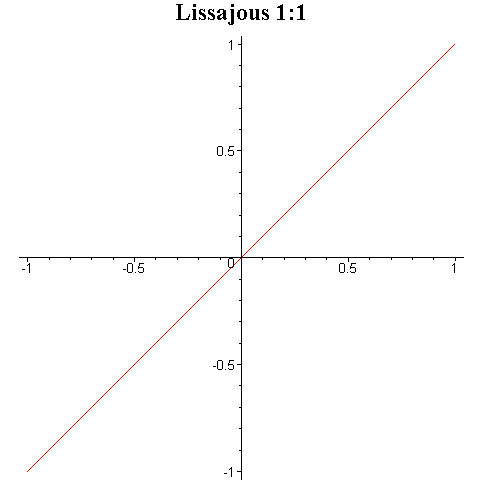
a) φ = 0. Równanie toru:

co jest równaniem prostej.

b) A_x = A_y; φ = ± π/2. Równanie toru:

czyli równanie okręgu o promieniu A.

c) A_x ≠ A_y; φ = ± π/2. Równanie toru:

jest równaniem elipsy, której osie są równoległe do osi układu odniesienia.

II. Częstotliwości kołowe są różne: ω_x ≠ ω_y

W tym przypadku ruch może być bardzo skomplikowany. Ogólnie, tor może nawet nie być krzywą zamkniętą, czyli, że ruch wtedy nie jest okresowy. Kiedy jednak stosunek obu częstotliwości kątowych ω_x / ω_y jest liczbą wymierną, czyli może być wyrażony przez stosunek dwóch liczb całkowitych, to tor ruchu jest krzywą zamkniętą, tzn. ruch jest okresowy, chociaż mimo to, często również bardzo skomplikowany.

Tego typu krzywe są znane pod nazwą krzywych Lissajous i niektóre z nich zostały przedstawione na rysunku poniżej.

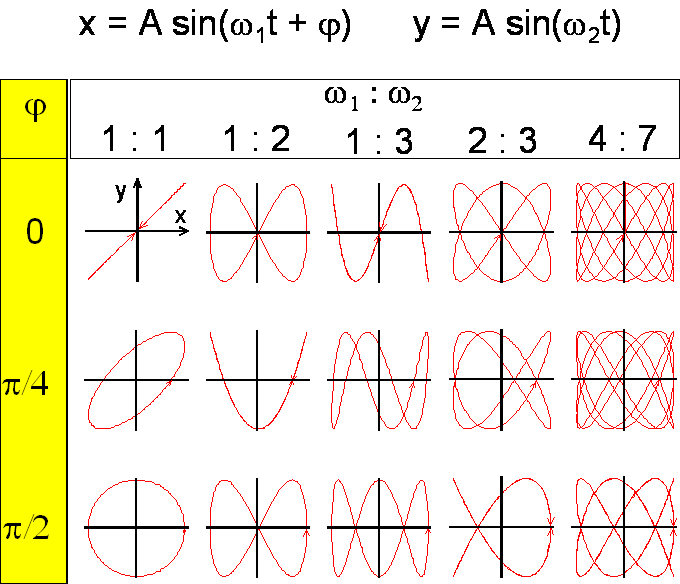
Przy ciągłej zmianie fazy φ krzyweLissajous zmieniają kształt dając wrażenie tańczenia w przestrzeni trójwymiarowej.

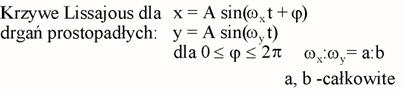
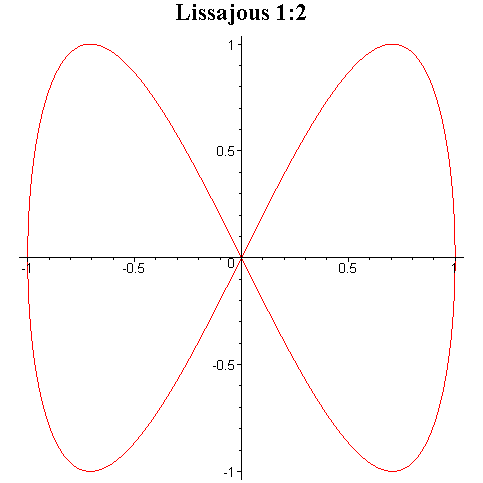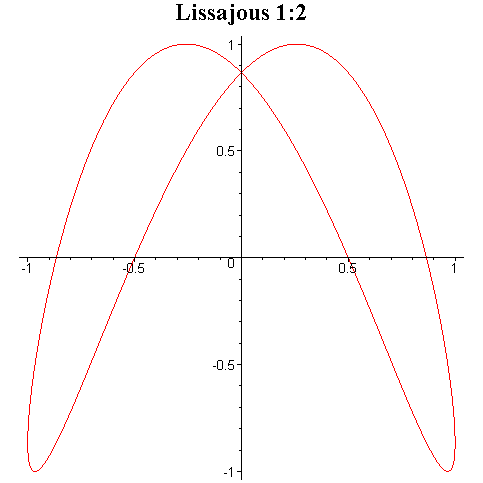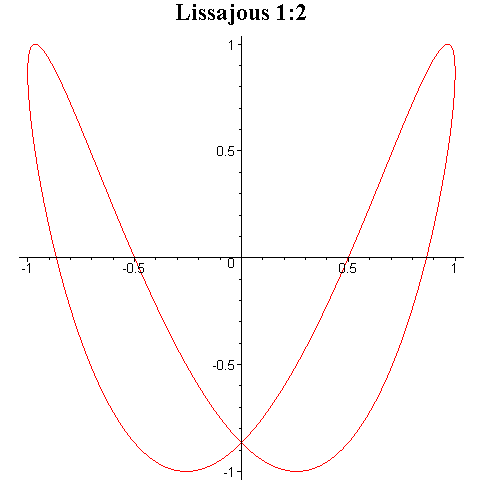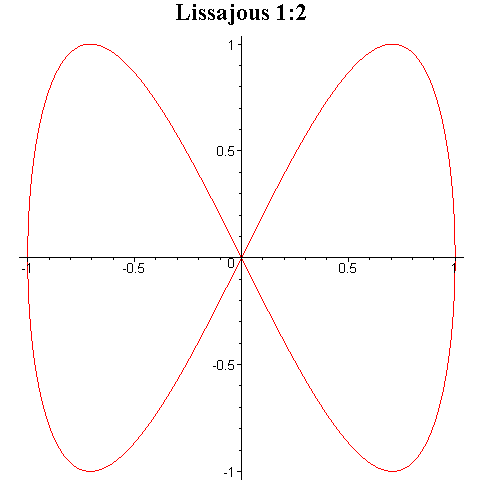
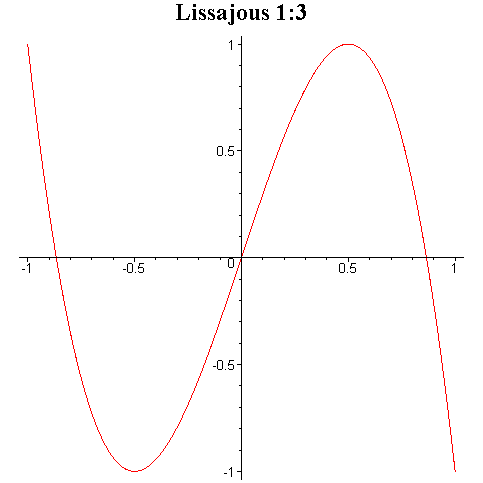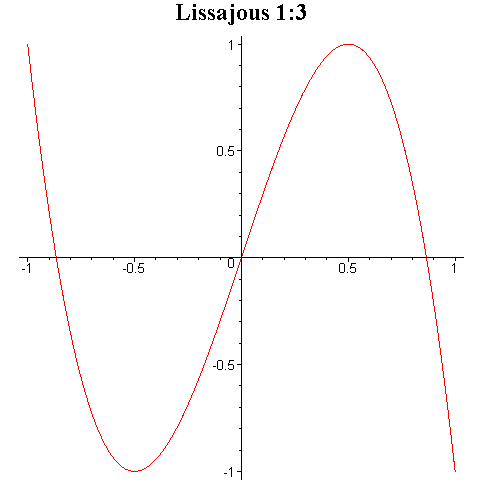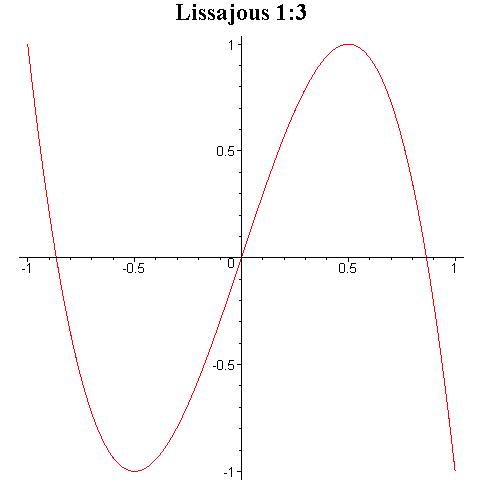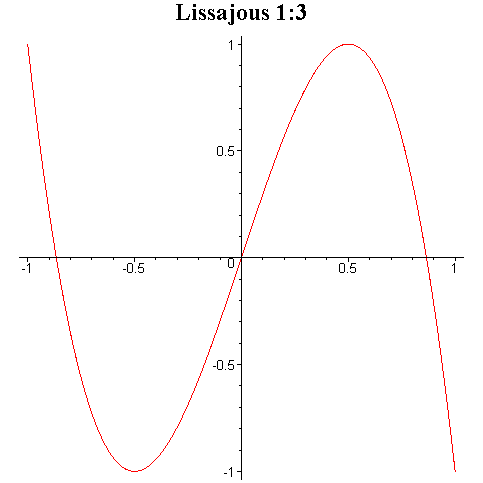
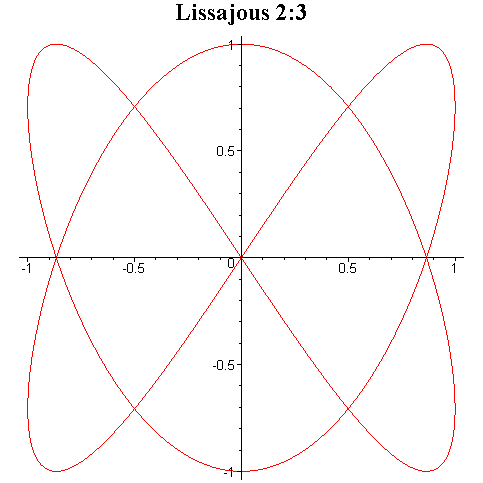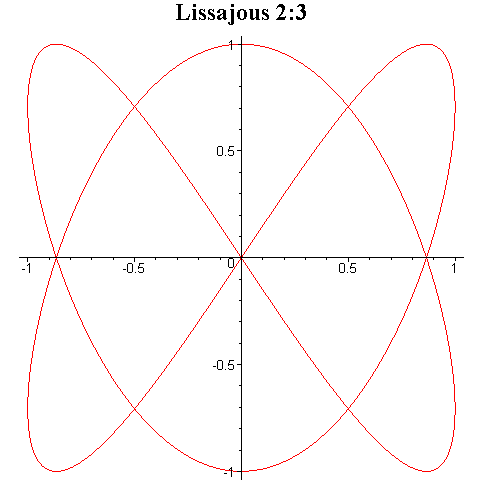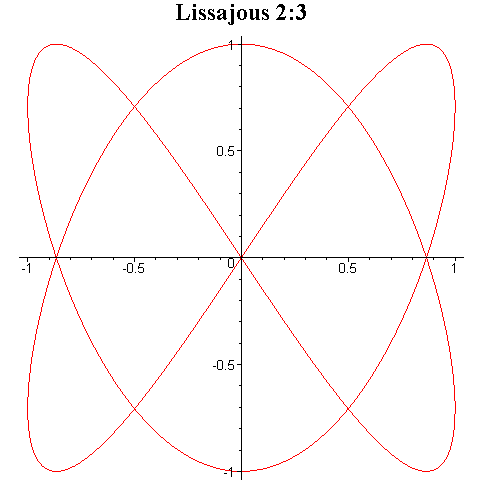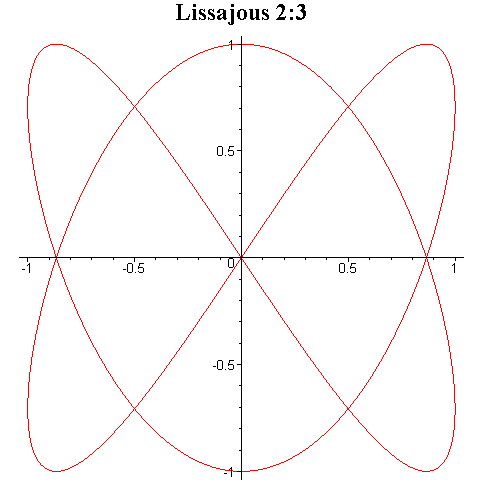
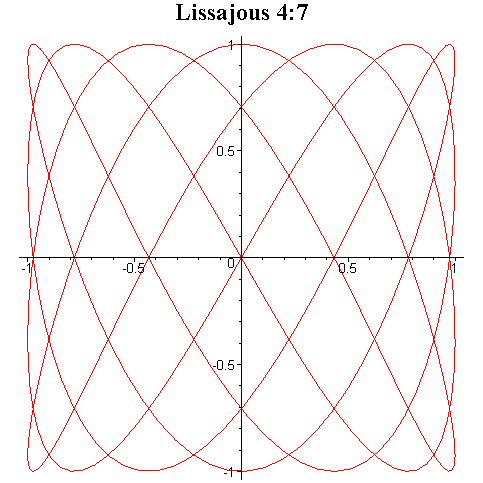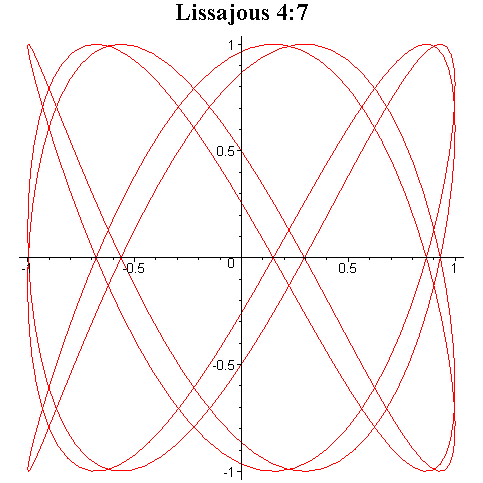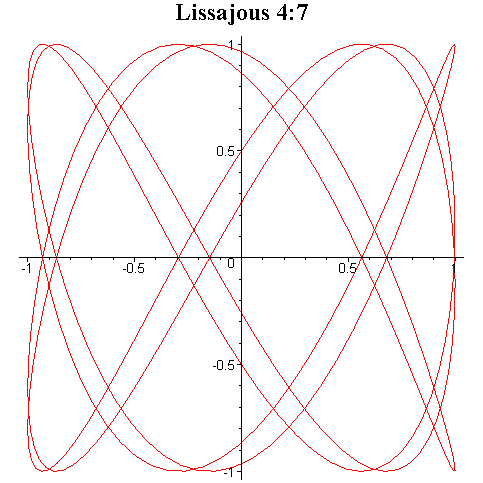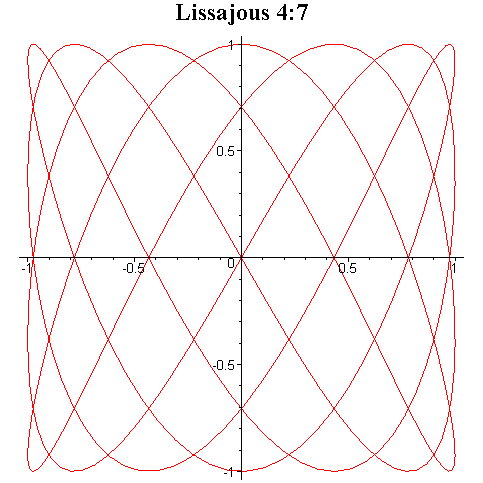
Interesujące efekty otrzymuje się przez składanie drgań prostopadłych, z których każde jest kombinacją liniową prostych drgań harmonicznych

Back to Index