Back to Index

PROSTE DRGANIA HARMONICZNE

Równanie różniczkowe. Energia drgań harmonicznych. Wahadło matematyczne. Wahadło fizyczne.

* Drgania swobodne

* Równanie różniczkowe opisujące drgania swobodne

* Energia drgań harmonicznych

* Wahadło matematyczne

* Wahadło fizyczne

Jak już wiemy, drgania harmoniczne, czyli drgania opisywane przez funkcje sinus lub cosinus, występują wtedy, gdy

1. ciało wykonujące takie drgania ma masę oraz
2. gdy na to ciało działa siła liniowo zależna (wprost proporcjonalna) od jego wychylenia z położenia równowagi i przeciwnie skierowana do tego wychylenia.

Najprostszy przypadek takich drgań występuje wtedy, gdy ciało raz wychylone z położenia równowagi zostaje pozostawione sobie, czyli wykonuje drgania kosztem nadanej mu energii początkowej. W takich drganiach, zwanych drganiami swobodnymi, na ciało nie działa żadna siła wymuszająca drgania, ani siła hamująca.

Przykładem ciała wykonującego proste drgania harmoniczne jest ciało przymocowane do sprężyny, która została początkowo ściśnięta lub rozciągnięta.

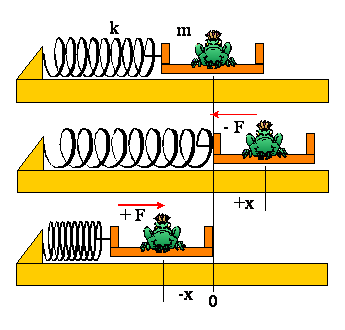
W tym przykładzie ciało o masie m porusza się wzdłuż linii prostej (osi x) i składowa siły F_x wzdłuż tej prostej jest elastyczną siłą zachowawczą (brak strat energii na tarcie): F_x = - kx

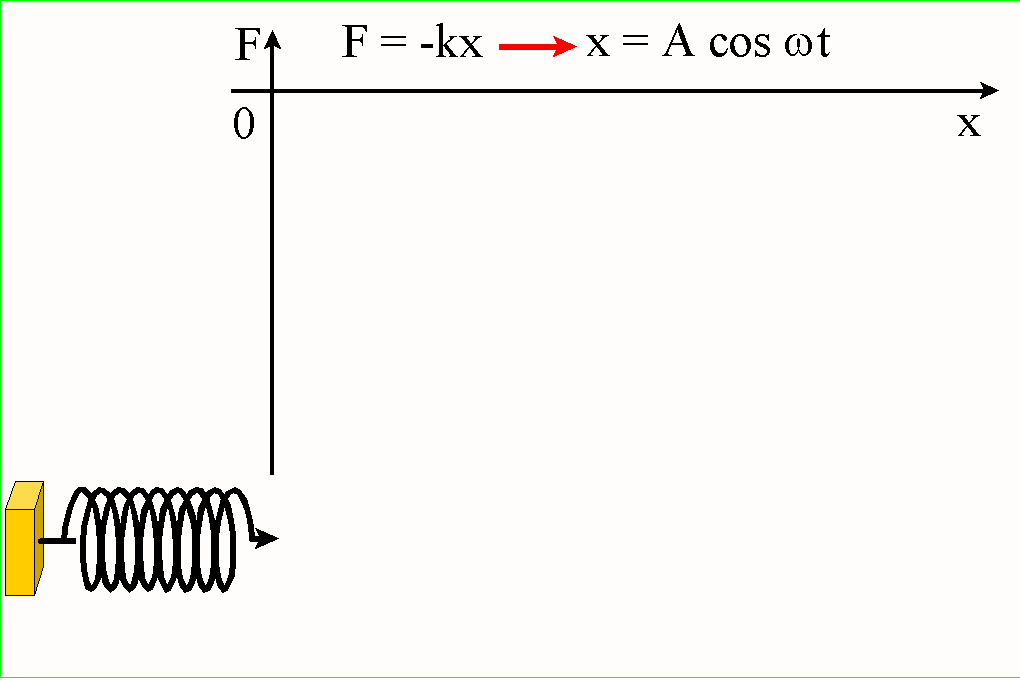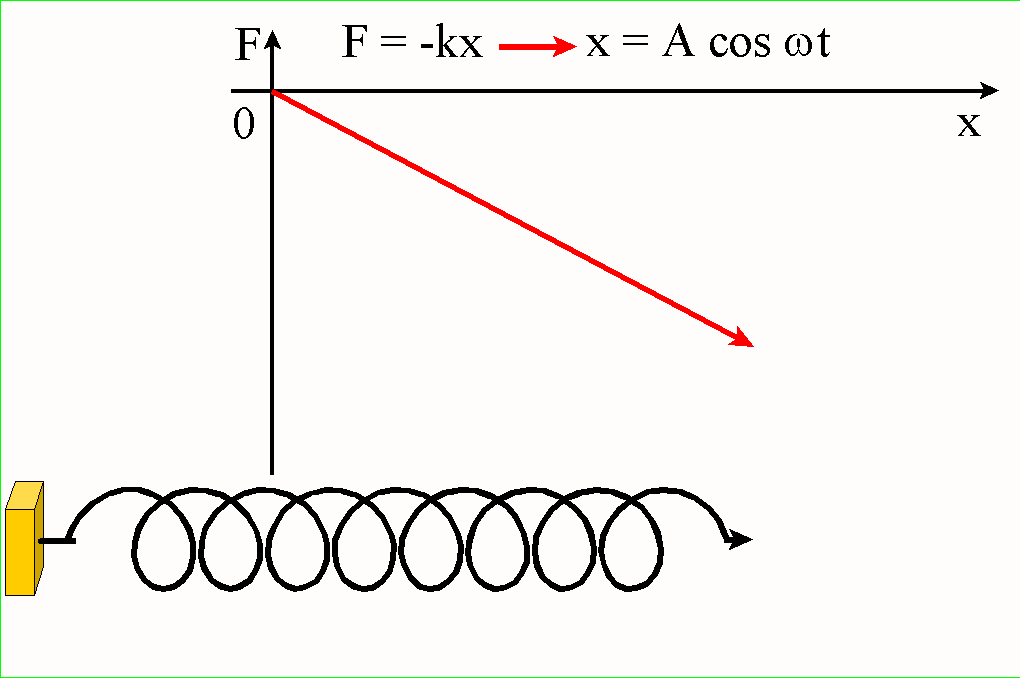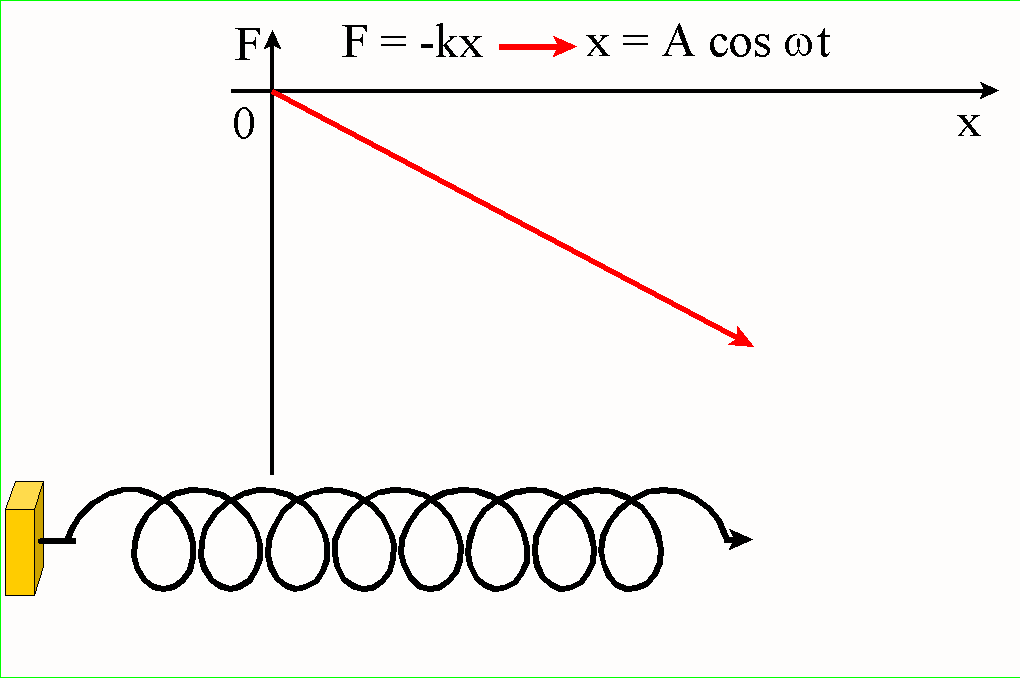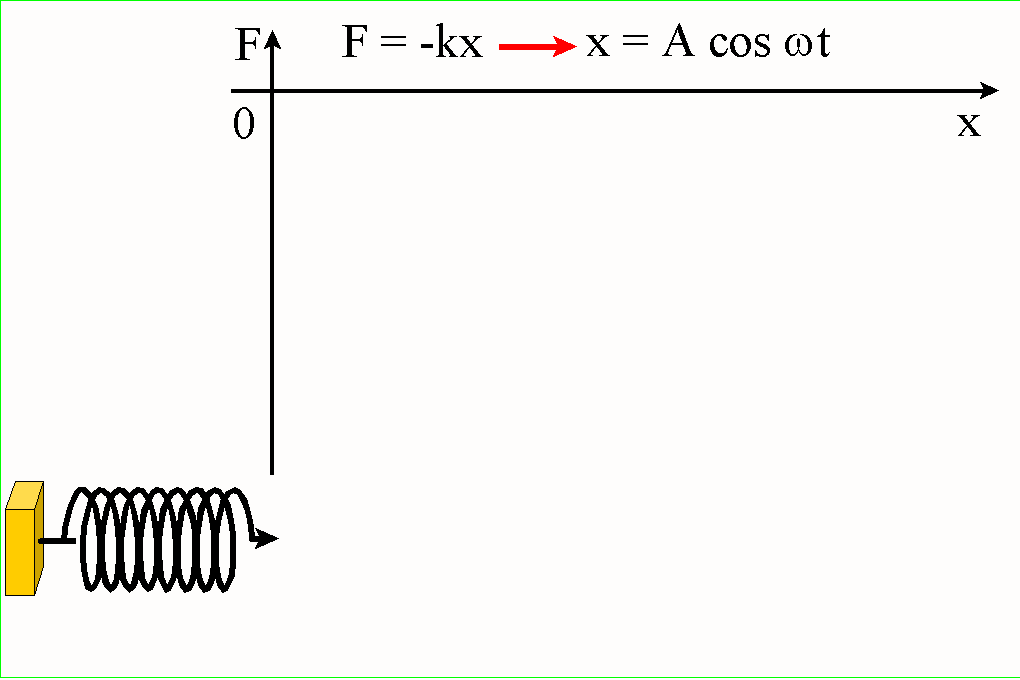
Ponieważ masa ciała m jest stała, to zamiast najogólniejszego drugiego prawa Newtona

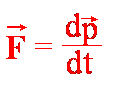
będziemy stosowali jego prostszą postać

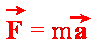
W tym przypadku siła zmienia się zgodnie z równaniem F = -kx, zatem drugie prawo Newtona zapiszemy jako

Stąd otrzymujemy

Oznaczamy k/m = ω₀² i równanie przyjmuje postać

Stosując podstawienie x = e^λt otrzymujemy równanie charakterystyczne

mające pierwiastki urojone

Rozwiązaniem ogólnym jest

Jednakże drgania odbywają się naprawdę i funkcja opisująca drgania musi być rzeczywista, zatem x = x* a stąd wynika, że stałe C₁ i C₂ muszą spełniać relację:

zatem

Wygodnie będzie użyć reprezentacji stałych C₁ i C₂ w postaci wykładniczej:

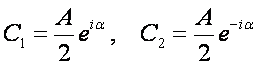
Stosując te stałe oraz wykorzystując wzór Eulera

otrzymujemy następujące rozwiązanie ogólne:

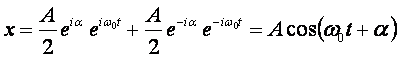
Zatem równaniem opisującym proste drgania harmoniczne jest równanie

lub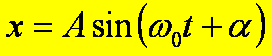

gdzie A jest amplitudą, ω₀t + α - fazą drgania, α - fazą początkową, ω₀ - częstotliwością kątową, która jest wyrażona przez stałą siłową k i masę układu drgającego m:

Ponieważ

to okres drgań swobodnych T wynosi

Dla drgań opisywanych równaniem

energia kinetyczna jest równa

Energia potencjalna jest równa pracy rozciągnięcia sprężyny na drodze x i wynosi

Stosując podstawienie

otrzymujemy wyrażenie na energię całkowitą ruchu harmonicznego

W drganiach swobodnych suma energii kinetycznej i potencjalnej jest stała (nie zależy od czasu). Należy przy tym zauważyć, że energia E jest proporcjonalna do kwadratu amplitudy A.

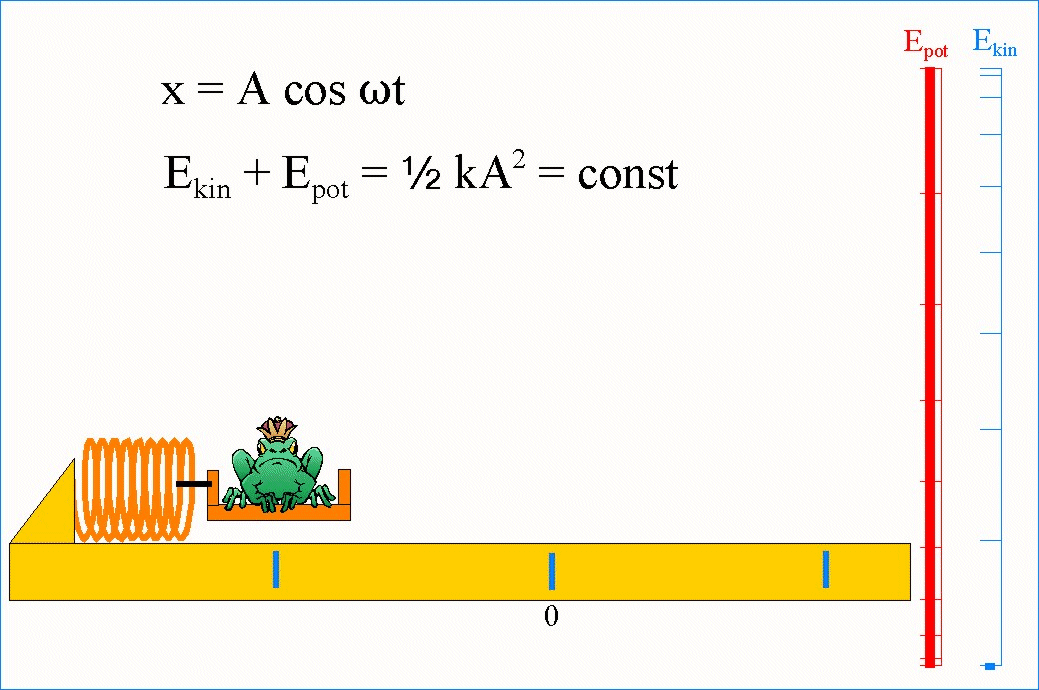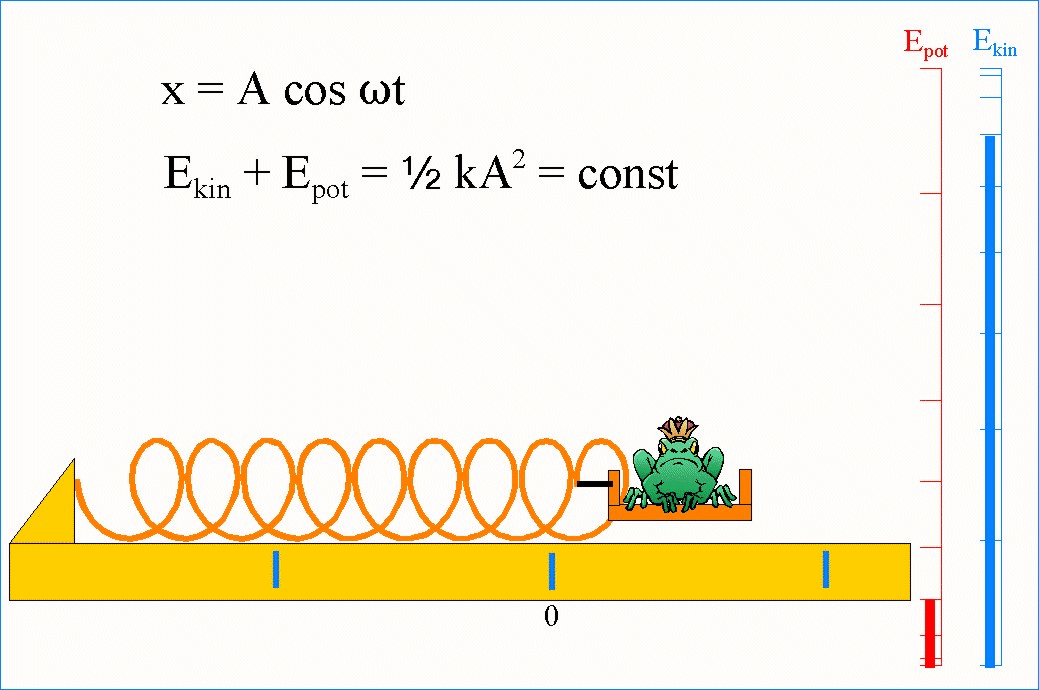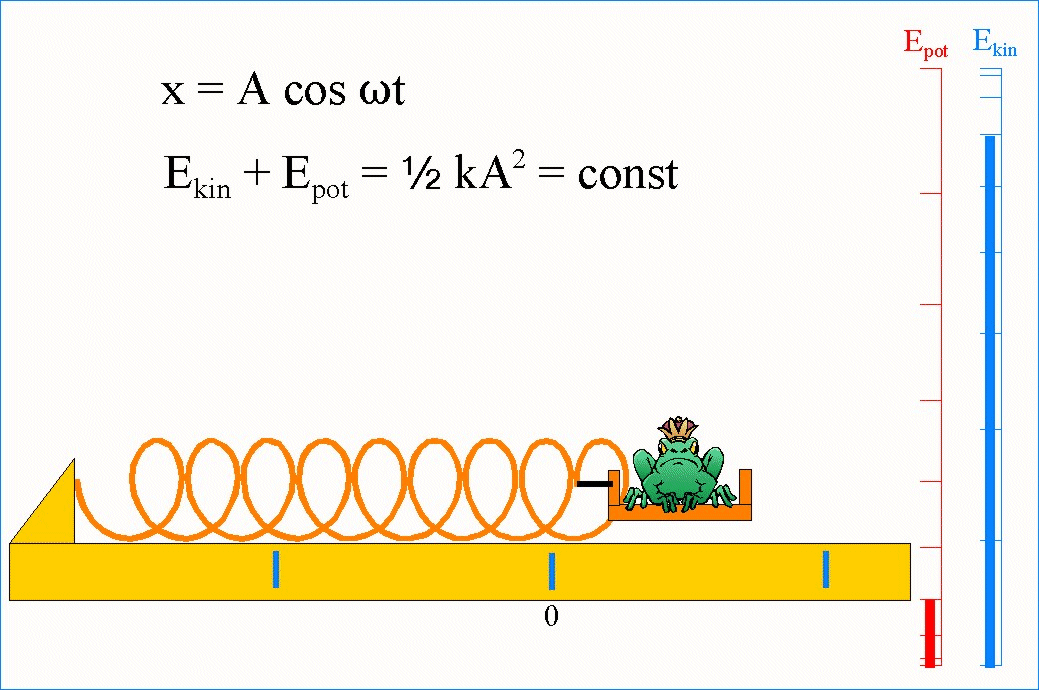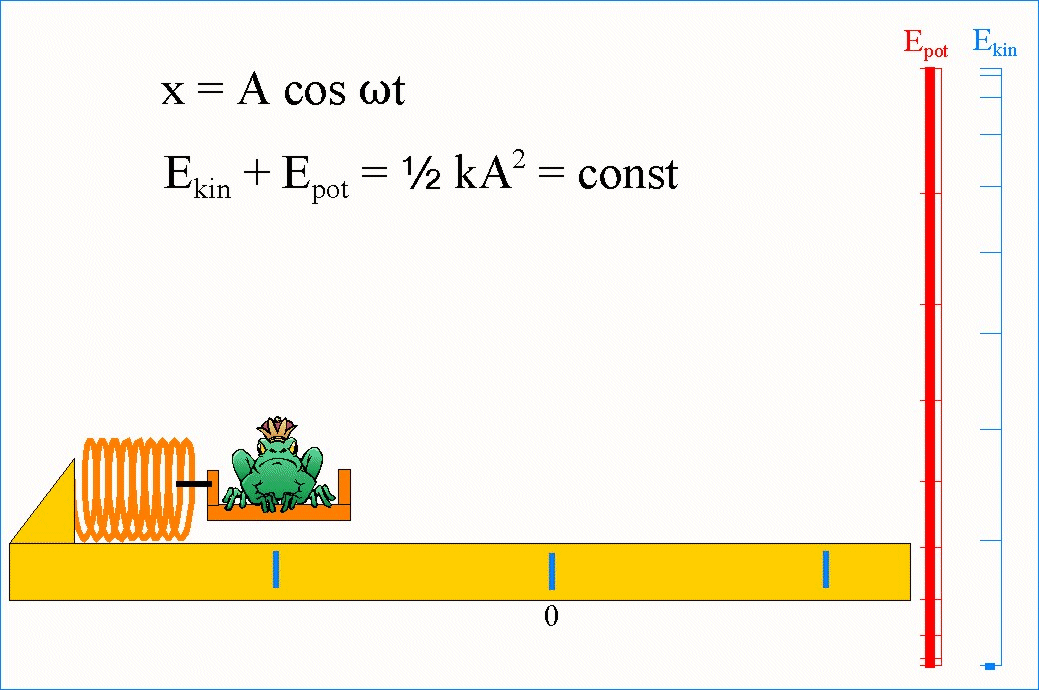
Należy zauważyć, że wzrost energii kinetycznej jest związany ze zmniejszaniem się energii potencjalnej.

ZASTOSOWANIA RÓWNANIA RÓŻNICZKOWEGO DLA DRGAŃ SWOBODNYCH:

WAHADŁO MATEMATYCZNE I WAHADŁO FIZYCZNE

Wahadło matematyczne (idealne) powstaje wtedy, gdy punkt materialny o masie m zostanie zawieszony na końcu nieważkiej nici o długości L. Po wychyleniu ze stanu równowagi pojawi się ruch wahadłowy.

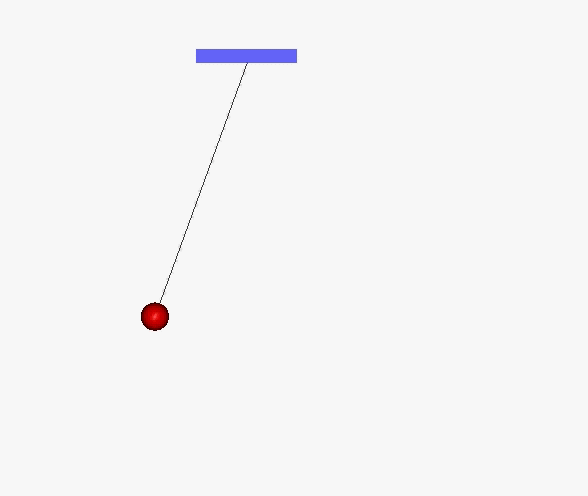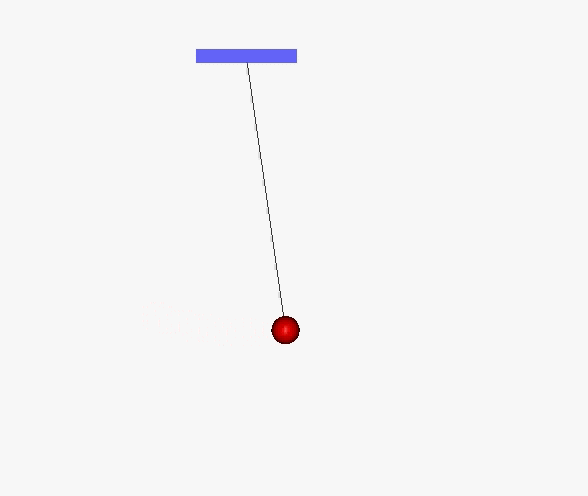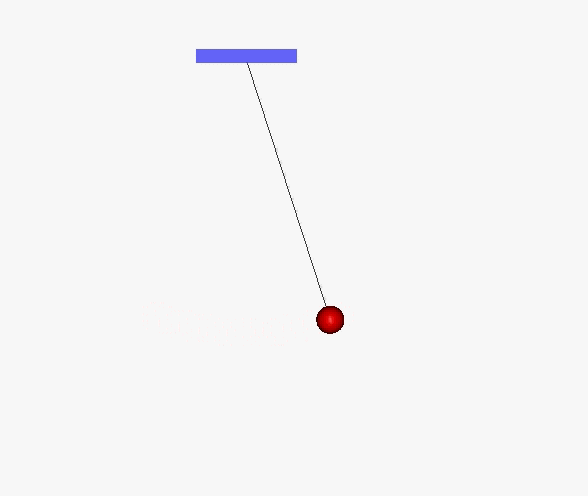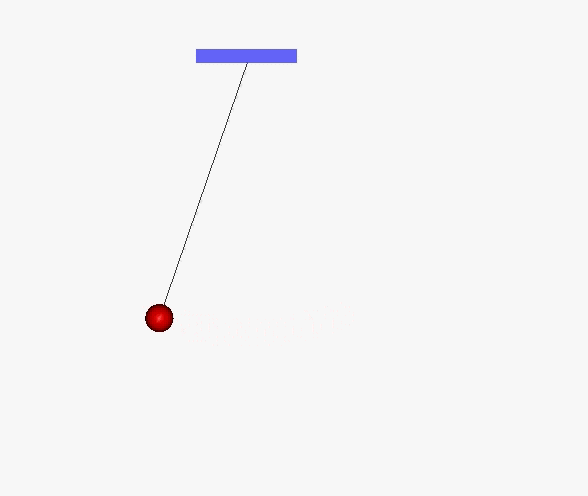
Ponieważ masa kulki jest stała, to podstawowym równaniem w tym zagadnieniu jest F = ma. Siła zwrotna j F = - mg sin θ jest składową siły grawitacji styczną do toru ruchu kulki.

Ponieważ kąt θ, który jest zmienną w naszym równaniu, występuje jako argument funkcji sinus, to otrzymalibyśmy równanie nieliniowe. Aby uwolnić się od nieliniowości przyjmujemy, że wahania odbywają się tylko dla małych kątów i wtedy dla małych wychyleń zastosujemy przybliżenie sin θ ≈ θ. Długość łuku drogi kulki x = Lθ, a zatem siła zwrotna F będzie określona przez równanie

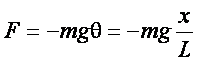
Na tej podstawie otrzymujemy równanie drgań wahadła matematycznego:

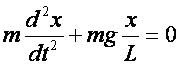czyli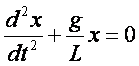

Otrzymane równanie jest analogiczne do równania drgań swobodnych

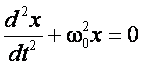
w którym ,a zatem nie ma powodów, aby go ponownie rozwiązywać. Od razu znajdujemy częstotliwość kątową

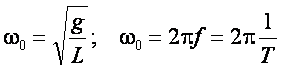
Ponieważ ω₀ = 2πf = 2π/T, to okres drgań T wahadła matematycznego jest

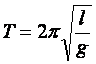
Ten rezultat nie jest szczególnie ważny, ale pouczające jest zastosowanie równania drgań swobodnych do badania tego typu prostych układów. To samo odnosi się do wahadła fizycznego.

Wahadłem fizycznym nazywamy bryłę sztywną o masie m, która została zawieszona powyżej jej środka masy.

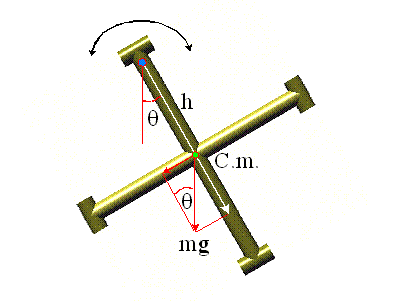
Po odchyleniu z położenia równowagi wystąpi ruch wahadłowy tej bryły sztywnej pod działaniem momentu siły grawitacji M. Zakładamy, że moment bezwładności tej bryły liczony względem osi przechodzącej przez punkt zawieszenia wynosi I. Ruch obrotowy bryły jest wywołany istnieniem niezerowego momentu siły ciężkości przyłożonej do środka masy. Podstawowym równaniem zaangażowanym tutaj jest zatem uproszczona druga zasada dynamiki dla ruchu obrotowego

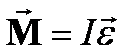
W przypadku wahadła fizycznego wartość momentu siły M jest

Aby uwolnić się od nieliniowości również i w tym przypadku, podobnie jak dla wahadła matematycznego, ograniczymy sie do małych wychyleń i zastosujemy przybliżenie sinθ ≈ θ. Teraz

Ponieważ M = Iε, to równanie ruchu przybiera postać

czyli

Jest to znowu równanie różniczkowe dla prostych drgań harmonicznych, w którym częstotliwość kątowa wynosi

Ponieważ ω₀ = 2πf = 2π/T, to okres drgań T wahadła fizycznego jest

Back to Index