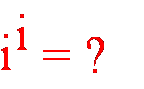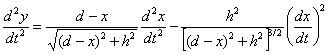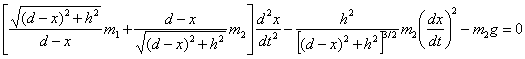Back to Index

WSTĘP DO ANALIZY DRGAŃ HARMONICZNYCH

Liczby zespolone. Równania różniczkowe.

* Liczby zespolone

* Postać algebraiczna i postać trygonometryczna liczby zespolonej

* Wzór Eulera i postać wykładnicza liczby zespolonej

* Operacje algebraiczne na liczbach zespolonych

* Wyprowadzenie wzoru Eulera

* Zastosowanie wzoru Eulera do otrzymywania wzorów na funkcje trygonometryczne sum i różnic kątów

* Równania różniczkowe zwyczajne o stałych współczynnikach

* Równania I-go rzędu: Przypadek zmiennych separowalnych

* Równania II-go rzędu o stałych współczynnikach

* - Równania jednorodne

* - Równania niejednorodne

* Nieliniowe równania różniczkowe

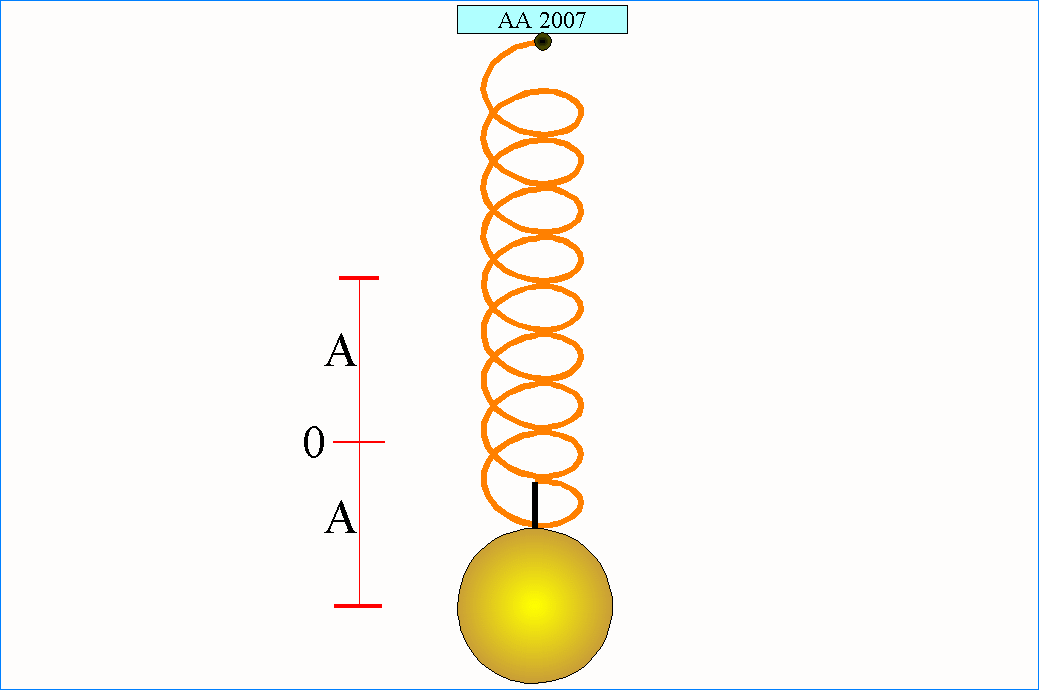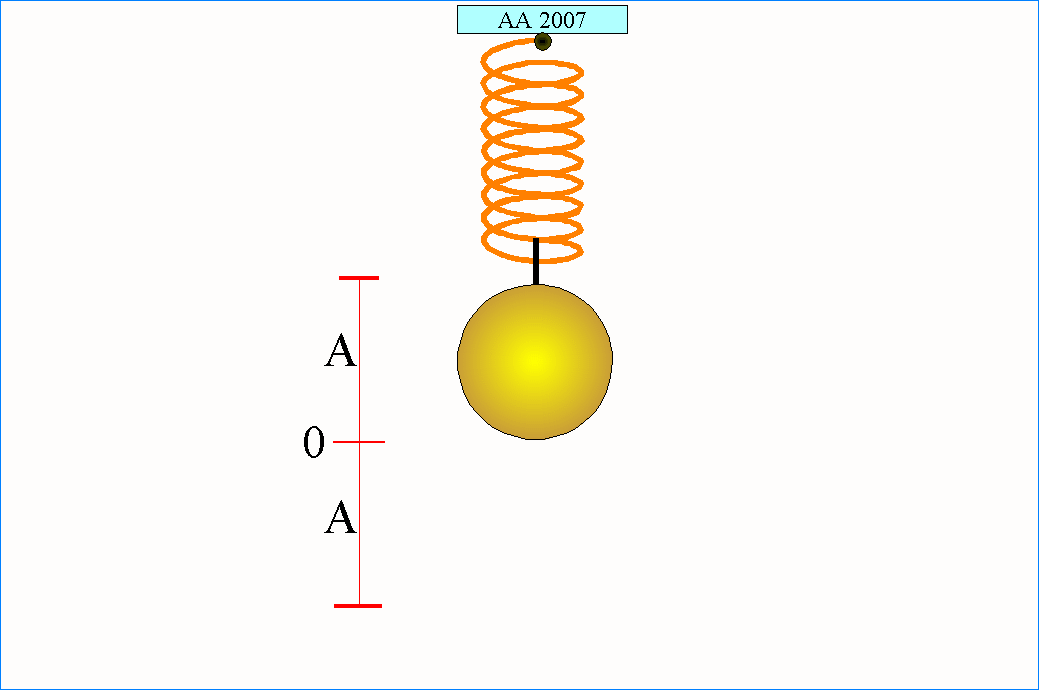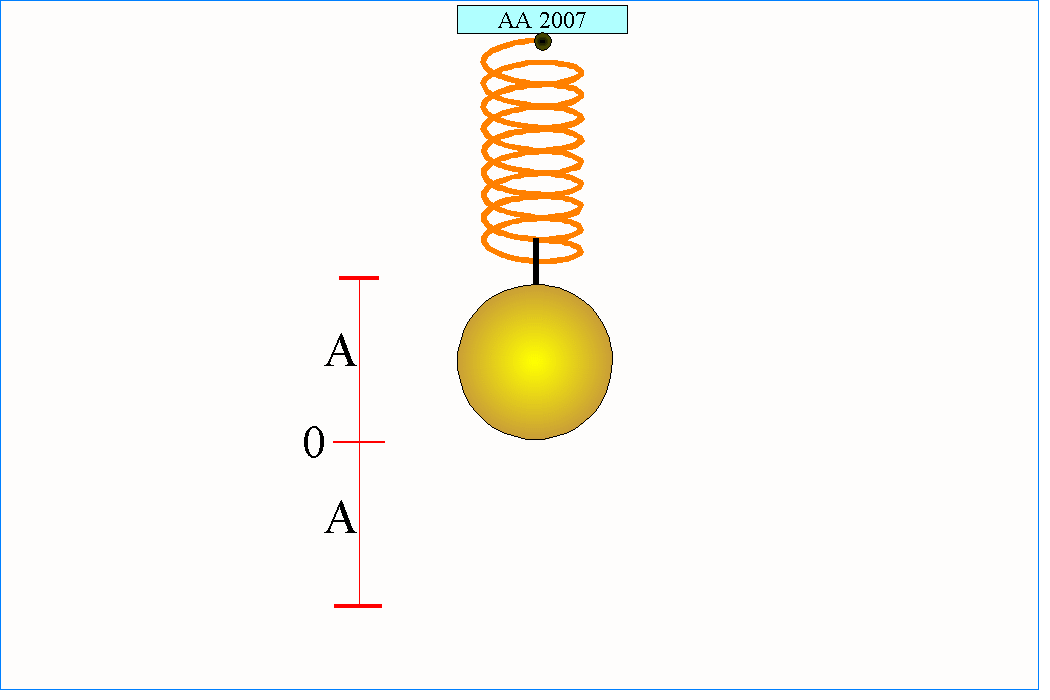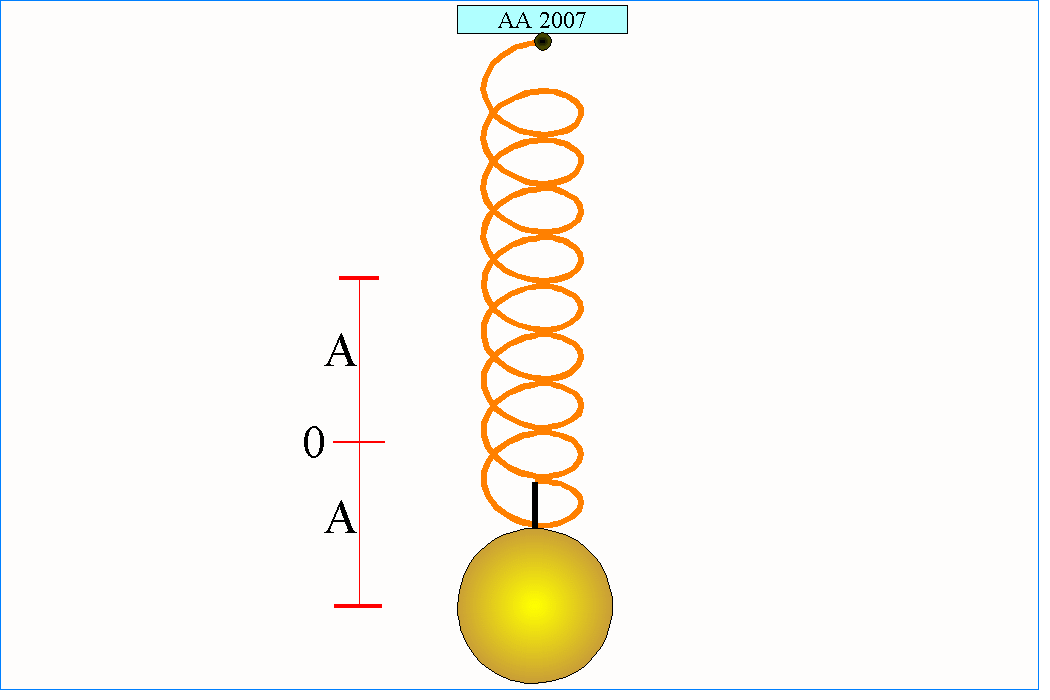
Drganiami harmonicznymi w mechanice nazywamy proste drgania okresowe, w których wychylenie jest opisywane funkcjami sinus lub cosinus. Ciało wykonujące takie drgania powinno spełniać dwa warunki:

1. musi mieć masę aby siłą bezwładności powrócić do stanu początkowego oraz

2. musi na to ciało działać siła zwrotna skierowana przeciwnie do kierunku odchylenia od stanu równowagi.

Proste drgania harmoniczne pojawia się w układzie złożonym z kulki o masie m przymocowanej do idealnej nieważkiej sprężyny. Stalowa kulka znajdująca się wewnątrz szkiełka zegarkowego też może wykonywać drgania w przybliżeniu harmoniczne, jeżeli zostanie wstępnie lekko poruszona. Ta sama kulka położona na wierzchołku odwróconego szkiełka zegarkowego po prostu z niego spadnie, ponieważ nie będzie w tym przypadku spełniony drugi z warunków (tym razem siła działająca na kulkę będzie zgodna z jej wychyleniem).

Dotychczas znane nam liczby całkowite, wymierne i niewymierne nazywamy liczbami rzeczywistymi i każdą z nich można przedstawić jako punkt na odpowiedniej osi liczbowej. Kiedy jednak liczba ma reprezentować pewną wartość złożoną z dwóch różnych wielkości, to taka liczba reprezentuje już punkt na specjalnej płaszczyźnie? Na przykład liczba „majątek” może składać się ze zmiennej „domy” i zmiennej „samochody”.

Wtedy: majątek = domy + samochody.

Aby na takich liczbach można było przeprowadzać operacje dodawania, odejmowania, mnożenia i dzielenia, to jedną ze składowych należy jakoś wyróżnić (np. zakolorować).

Jeżeli analizujemy dwie grupy ludzi z₁ i z₂, to może być istotne ile każda z tych grup zawiera mężczyzn i ile kobiet.

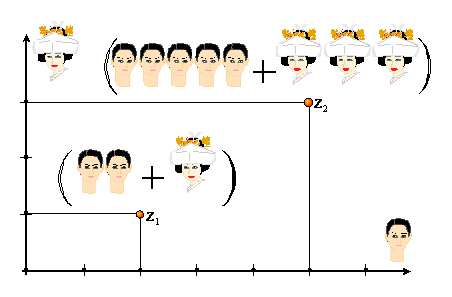
Obie grupy przedstawiliśmy na płaszczyźnie, na której jedna z osi reprezentuje mężczyzn, a druga z osi – kobiety. Pewnym uproszczeniem byłoby zastosowanie liczb oznaczających mężczyzn i oddzielnie kobiety:

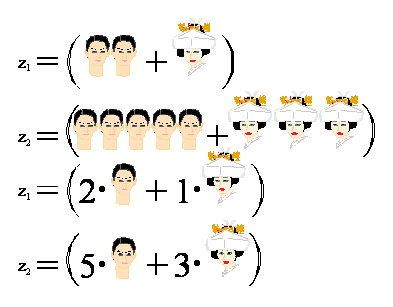
Ciągle jednak nie uniknęliśmy malowania symboli twarzy. Genialnym pomysłem było zastosowanie liczby urojonej „i”:

która posłuży do „zakolorowania” liczby oznaczającej kobiety, co pozwoli nam na radykalne uproszczenie zapisu. Naga liczba będzie teraz oznaczała mężczyzn, zakolorowana – kobiety:

Liczba „i” jest jednostką urojoną i każda liczba zakolorowana tą jednostką staje się liczbą urojoną. Liczba będąca sumą liczb rzeczywistej i urojonej nosi nazwę liczby zespolonej i jest tradycyjnie oznaczana literą z.

Np. w liczbie z = 10 + 3i liczba 10 jest częścią rzeczywistą liczby z, oznaczaną przez Re z (od realis), a liczba 3i jest częścią urojoną liczby z, oznaczaną przez Im z (od imaginarius). Nazwa ‘urojona’ jednostki „i” pochodzi z jej określenia jako pierwiastka kwadratowego z „-1”:

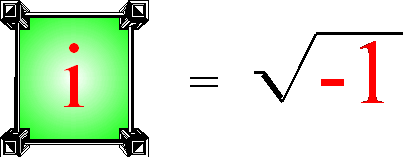
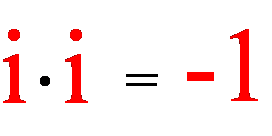
Liczbą zespoloną nazywamy zatem liczbę o postaci

gdzie x i y są liczbami rzeczywistymi; liczbę x nazywamy częścią rzeczywistą liczby zespolonej, Re z, zaś liczbę y - jej częścią urojoną, Im z. Liczba

jest nazywana liczbą sprzężoną do liczby z. Łatwo zauważyć, że

Liczby zespolone mają prostą interpretację geometryczną. Liczbę zespoloną z = x + iy traktujemy jako punkt na pewnej płaszczyźnie.

Płaszczyzna, której jedna z osi układu określa wartości urojone a druga oś – wartości rzeczywiste, jest nazywana płaszczyzną zespoloną lub płaszczyzną Arganda:

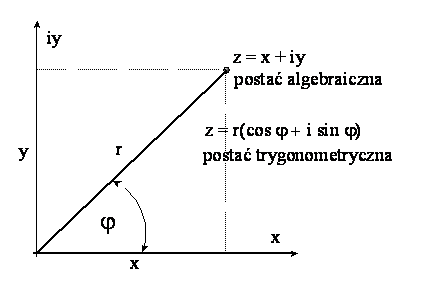
Każdy punkt na tej płaszczyźnie oznacza jedna liczbę zespoloną. Promień r łączący początek układu z liczbą z nazywamy modułem liczby z. Moduł r reprezentuje bezwzględną wartość liczby zespolonej

Kąt φ między osią z, a promieniem r nazywamy argumentem liczby z. Postać liczby zespolonej z = x + iy nosi nazwę postaci algebraicznej. Liczbę zespoloną można także przedstawić w postaci trygonometrycznej (we współrzędnych biegunowych) korzystając z jej modułu i argumentu. Ponieważ x = r cos φ oraz y = r sin φ, to każdą liczbę zespoloną można przedstawić w dwóch równoważnych postaciach: algebraicznej i trygonometrycznej

Dwie liczby zespolone z₁ = x₁ + i y₁ oraz z₂ = x₂ + i y₂ są równe wtedy, gdy ich moduły są równe, r₁ = r₂, a ich argumenty mogą się różnić tylko o całkowitą wielokrotność 2π:

Wspaniałą i niezwykle użyteczną relacją między funkcjami trygonometrycznymi i wykładniczymi w dziedzinie zespolonej jest wzór Eulera:

Stosując wzór Eulera automatycznie otrzymujemy postać wykładniczą liczby zespolonej

Dodawanie (odejmowanie) liczb zespolonych: Liczby zespolone dodajemy do siebie w ten sposób, że oddzielnie dodajemy części rzeczywiste i oddzielnie urojone. Odejmowanie przeprowadzamy analogicznie.

Mnożenie, dzielenie i potęgowanie liczb zespolonych w postaci trygonometrycznej:

Mnożąc wielokrotnie tę samą liczbę przez siebie otrzymujemy potęgę liczby zespolonej (tzw. wzór de Moivre'a):

Przez zastosowanie postaci wykładniczej liczb zespolonych operacje mnożenia i dzielenia tych liczb stają się dziecinnie proste

Mnożąc liczbę z przez sprzężoną do niej z* otrzymujemy zawsze kwadrat modułu liczby r² niezależnie od postaci liczby z (algebraicznej, trygonometrycznej, czy wykładniczej)

Z okazji roku 2000 ogłoszono konkurs na najpiękniejszy wzór matematyki. Wygrał wzór

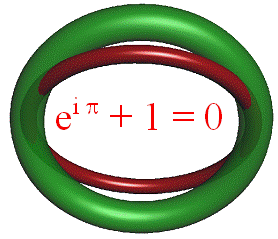
Chyba już wiesz, jak ten wzór powstał ?

Zagadka. Po przeczytaniu powyższych informacji na temat liczb zespolonych nietrudno będzie odpowiedzieć na pytanie, jaki jest wynik przedstawionego potęgowania

Zdziwisz się, ale wynikiem jest liczba rzeczywista!

Wyprowadzenie wzoru Eulera

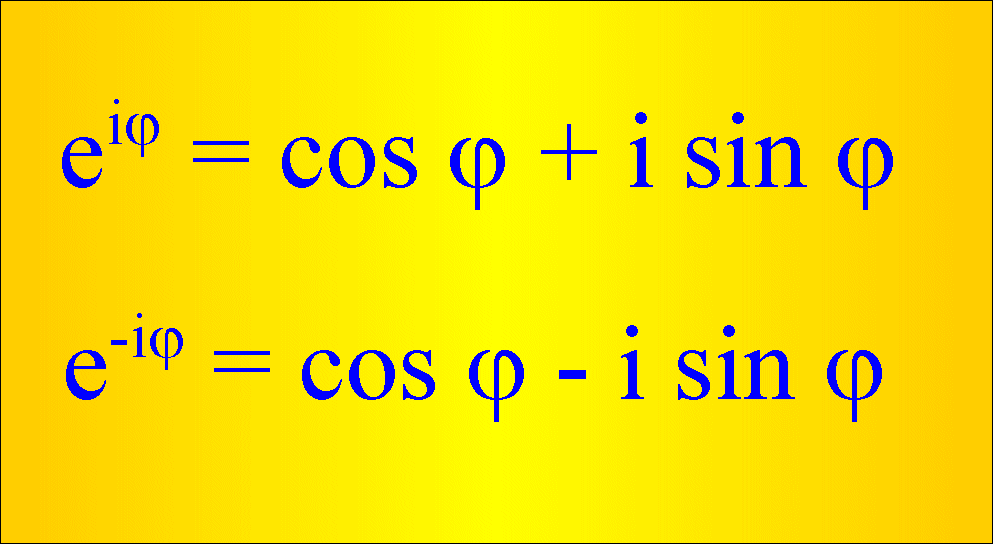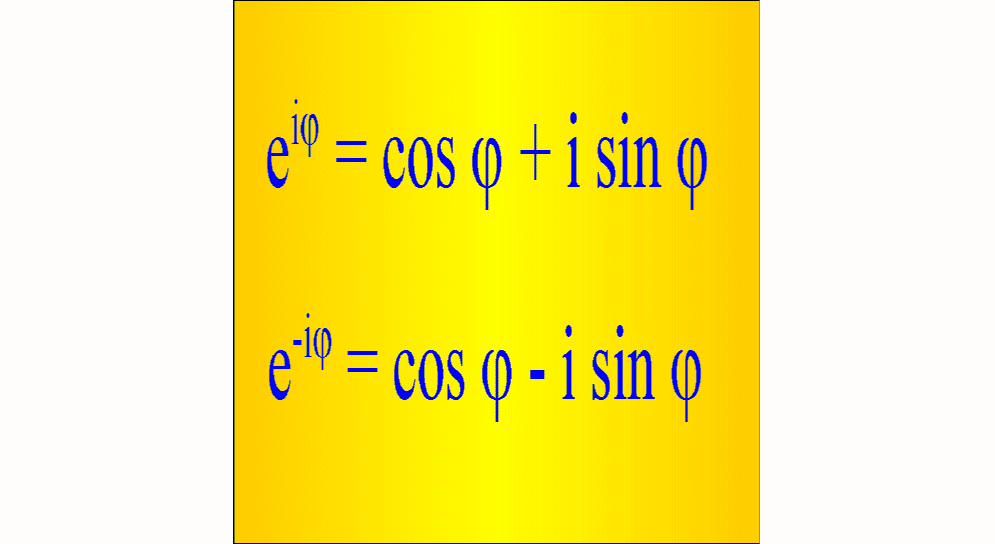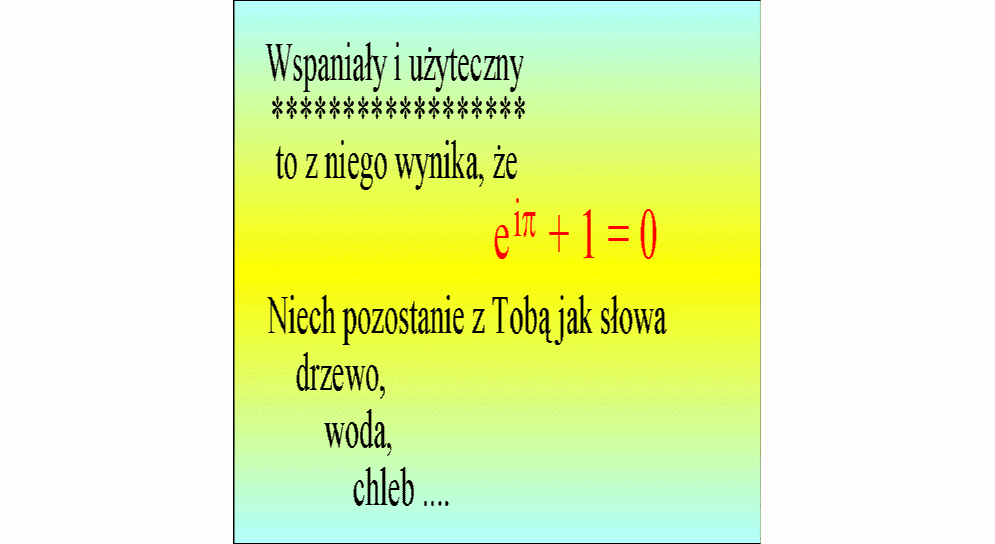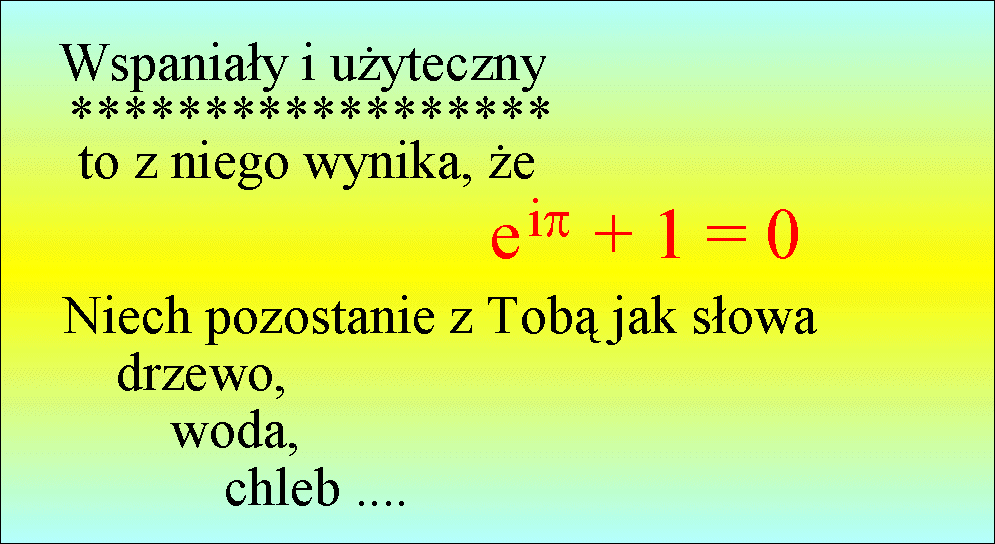
Tajemniczo wyglądający wzór Eulera można łatwo wyprowadzić. Rozwijając w szereg Maclaurina

funkcje sin x i cos x otrzymujemy:

Jeżeli teraz rozwiniemy w szereg Maclaurina funkcję exp(ix), to otrzymamy

co jest sumą rozwinięcia funkcji cos x oraz pomnożonemu przez i rozwinięcia funkcji sin x :

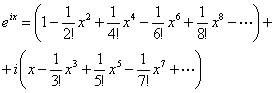
W ten sposób otrzymujemy wzór Eulera:

Analogicznie otrzymamy:

Łatwo otrzymać odwrotne związki:

Zastosowanie wzoru Eulera do otrzymywania wzorów na funkcje trygonometryczne sum i różnic kątów

Prostym, ale interesującym zastosowaniem wzoru Eulera jest otrzymywanie wzorów na funkcje trygonometryczne sum i różnic kątów. Gdy chcemy otrzymać np. wzór zastępujący cos(a+b), to stosujemy wzór, który otrzymamy łatwo ze wzoru Eulera

i zapisujemy go dla przypadku, gdy x = a + b, czyli

Przekształcamy prawą stronę i stosujemy wzór Eulera do poszczególnych składników

Ostatecznie otrzymujemy poszukiwany wzór

Wzór ten będziemy wykorzystywali w opisie składania drgań harmonicznych.

Można to też zrobić następująco: Gdy chcemy otrzymać np. sin(a+b), wtedy wypisujemy wzór Eulera, w którym wystąpi sin(a+b):

Lewą stronę przekształcamy jako

i dalej

Grupujemy razem części rzeczywiste i urojone i porównujemy ze wzorem wyjściowym

Porównujemy części rzeczywiste i części urojone z obu stron równania i otrzymujemy szukane wzory:

RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE O STAŁYCH WSPÓŁCZYNNIKACH

Ogólnie, równanie różniczkowe wiąże ze sobą zmienną niezależną t, poszukiwaną funkcję x oraz jej pochodne x’, x’’, x’’’ ...

Tutaj zajmiemy się tylko takimi równaniami, które będą nam potrzebne do analizy drgań harmonicznych w mechanice i w elektrodynamice. Równania różniczkowe cząstkowe, występujące w opisie ruchu falowego, zostaną przedstawione fragmentarycznie w wykładzie na temat tego ruchu.

Rzędem równania różniczkowego jest rząd najwyższej pochodnej, jaka występuje w równaniu.

Jeżeli w równaniu pierwszego rzędu

funkcja f(t, x) może zostać przedstawiona jako iloczyn funkcji g(t) i h(x) będących funkcjami tylko t i tylko x, odpowiednio, to mówimy, że jest to równanie o zmiennych separowalnych. Zatem zmienne x i t w równaniu

mogą zostać rozdzielone:

Pozostaje tylko oddzielnie scałkować obie strony tego równania:

Równanie typu

gdzie a i b są stałymi zaś f(t) jest znaną funkcją t jest nazywane liniowym równaniem różniczkowym drugiego rzędu o stałych współczynnikach.

Jeżeli f(t) nie zależy od t (jest pewna stałą), wtedy równanie jest nazywane jednorodnym równaniem różniczkowym, w przeciwnym razie równanie jest niejednorodne.

Są to równania o postaci

Dowolna funkcja x(t) spełniająca równanie jest nazywana rozwiązaniem szczególnym tego równania. Równanie drugiego rzędu ma dwa takie rozwiązania szczególne x₁(t) i x₂(t). Kombinacja liniowa rozwiązań szczególnych jest rozwiązaniem ogólnym x równania różniczkowego

gdzie C₁ i C₂ są dowolnymi stałymi.

W ogólnym przypadku równania jednorodnego rozwiązanie otrzymujemy przez zastosowanie podstawienia

Przy tym podstawieniu otrzymujemy

Po podstawieniu do pierwotnego równania różniczkowego i po uproszczeniu otrzymujemy równanie

zwane równaniem charakterystycznym. Jeżeli pierwiastki równania charakterystycznego λ₁ i λ₂ są różne, wtedy funkcje

są rozwiązaniami szczególnymi równania d²x/dt² + a dx/dt +bx = 0. Rozwiązaniem ogólnym jest dowolna kombinacja liniowa rozwiązań szczególnych

Kiedy pierwiastki równania charakterystycznego są równe, λ₁ = λ₂ = λ , wtedy

i rozwiązanie ogólne ma postać

Kiedy prawa strona równania

jest funkcją zmiennej niezależnej t, to równanie jest niejednorodne.

Rozwiązanie ogólne równania niejednorodnego jest sumą rozwiązania ogólnego równania jednorodnego i dowolnego rozwiązania szczególnego równania niejednorodnego

Ponieważ nie ma ogólnej metody znajdowania rozwiązania szczególnego równania niejednorodnego, to tylko od naszych umiejętności i szczęścia będzie zależało, czy będziemy w stanie go znaleźć.

Nieliniowe równania różniczkowe

Bardzo często proste sytuacje fizyczne prowadzą do zagadnień, które są opisywane przez nieliniowe równania różniczkowe. Równania takie zwykle nie mają rozwiązań analitycznych i konieczne jest wtedy stosowanie metod numerycznych. Przykładem może być proste zadanie wzięte z książki F. Y. Wang – Physics with Maple, Wiley.

Wózek o masie m₁ jest uwolniony ze stanu spoczynku w punkcie x = 0 i w czasie t = 0 i jest ciągnięty po stole przez inną masę m₂ spuszczaną pionowo, jak pokazano na rysunku

Przyjmując, że na powierzchni stołu i na bloku nie występuje tarcie, znaleźć położenie masy m₁ jako funkcję czasu.

Rozwiązanie. Kąt θ określamy z geometrii układu

(1)

Ponieważ kąt θ zmienia się w czasie, to równie w czasie zmienia się siła działająca na m₁. Niech naprężenie nici wynosi T, wtedy równanie ruchu dla m₁ jest określone przez drugie prawo Newtona

(2)

a dla masy m₂

(3)

Długość nici l jest stała (jest to narzucone ograniczenie ruchu)

Stąd wyznaczymy drugą pochodną występująca w równaniu (3):

Eliminując T z równań (2) i (3), otrzymujemy

Podstawiając za cos θ i za otrzymane wyrażenia tworzymy równanie różniczkowe drugiego rzędu opisujące ruch masy m₁:

(4)

dla którego warunkami początkowymi są

Ponieważ to równanie różniczkowe opisujące prostą sytuację nie ma rozwiązania analitycznego, to musimy się posłużyć dla jego rozwiązania metodami numerycznymi.

Back to Index