MOMENT SIŁY
Praca i
moc w ruchu obrotowym.
* Praca i moc w ruchu obrotowym
W ruchach obrotowych ważne są nie tylko same wielkości fizyczne, ale i sposób ich usytuowania względem osi obrotu, czyli ich momenty. Wiemy już, że w ruchu obrotowym ważna jest nie tylko masa, ale też moment bezwładności I. W przypadku siły, jej skuteczność na wywołanie przyśpieszenia jest określona przez sposób przyłożenia tej siły względem osi obrotu.
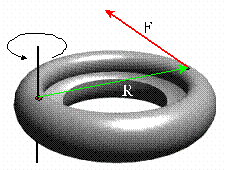
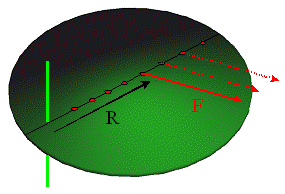
Relację między siłą i sposobem jej przyłożenia opisuje
elegancko MOMENT SIŁY. Momentem siły nazywamy iloczyn wektorowy ramienia działania
siły R i wektora siły F:
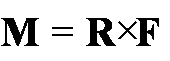
o wartości
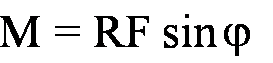
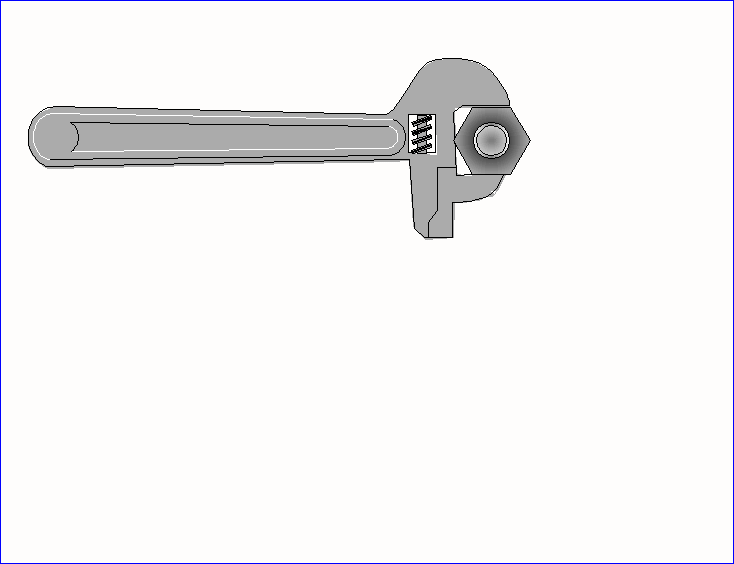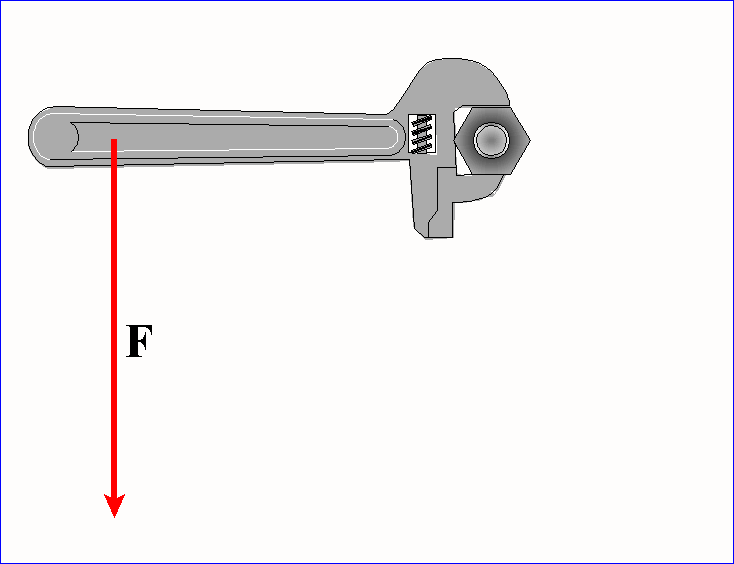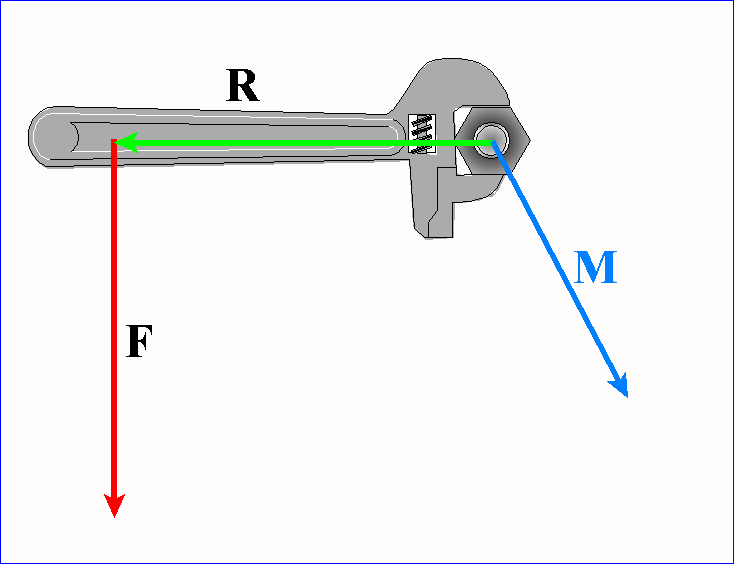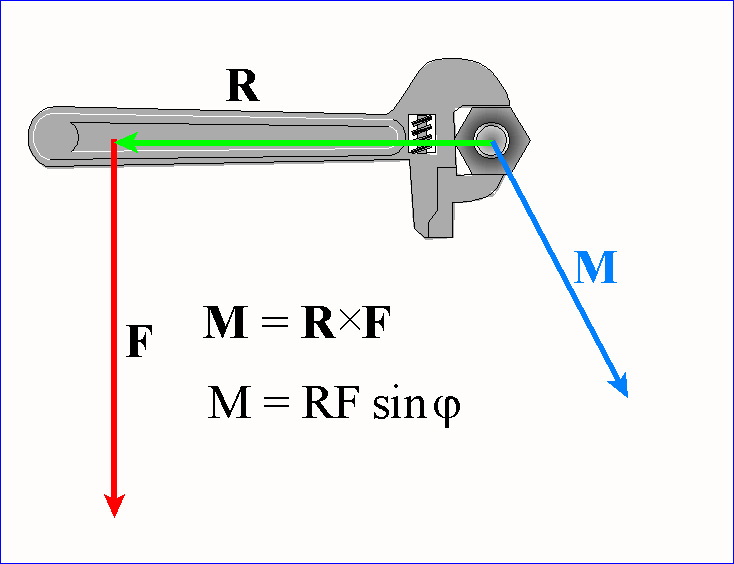
Jak w każdym iloczynie wektorowym, tak i tutaj
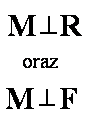
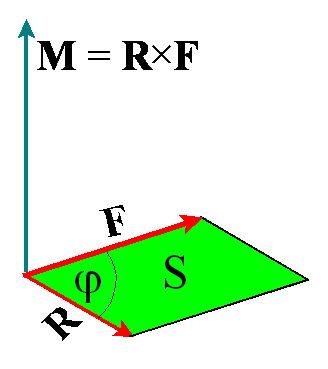
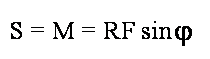
Siła, zatem, nie wywoła żadnego skutku na ruch obrotowy kiedy kąt między wektorami siły F i ramienia R wynosi 0o lub 180o. Jaki jest skutek przyłożenia momentu siły M ?
Stosujemy II. prawo ruchu Newtona i relację między prędkościami linową i kątową v = Rω w postaci skalarnej, słusznej kiedy wektory R i ω są do siebie prostopadłe
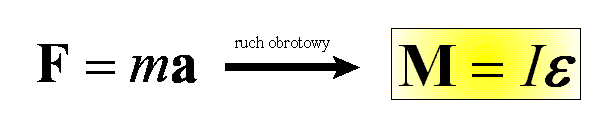
Po pomnożeniu obu stron równania przez R otrzymamy 
. Ponieważ mR2 = I, to wnioskujemy, że
Powyższa zależność jest również
słuszna dla przypadku bryły materialnej. Zauważmy, że podczas gdy siła
zewnętrzna nadaje przyśpieszenie liniowe a, to moment siły zewnętrznej
nadaje przyśpieszenie kątowe ε.
Praca w ruchu liniowym jest określona przez ogólne wyrażenie
ale w ruchu obrotowym 
, a zatem 
. Na podstawie własności iloczynu mieszanego trzech wektorów
możemy napisać
Na pracę w ruchu obrotowym otrzymaliśmy więc wyrażenie
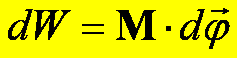
Moc w ruchu obrotowym
czyli
