MOMENT BEZWŁADNOŚCI
Główne
osie bezwładności. Energia kinetyczna ruchu obrotowego.
* Moment bezwładności układu punktów materialnych
* Moment bezwładności brył sztywnych
* Przykłady obliczania momentów bezwładności
* Główne
osie bezwładności – elipsoida bezwładności
* Energia kinetyczna ruchu obrotowego

Moment bezwładności punktu materialnego lub bryły sztywnej pełni w ruchu obrotowym dokładnie tę samą rolę, jak masa tych ciał w ruchu postępowym. Moment bezwładności, który oznaczamy dużą literą I (od inertia), opisuje sposób rozkładu masy wokół osi obrotu. Im dalej masa jest rozłożona wokół osi obrotu, tym większy jest jej moment bezwładności I. Moment bezwładności jest zawsze funkcją kwadratu odległości elementów masy od osi obrotu i dla pojedynczego punktu o masie m obracającego się w odległości R
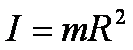

W przypadku wielu punktów, ich łączny moment bezwładności jest sumą momentów poszczególnych punktów (moment bezwładności jest wielkością addytywną):
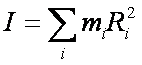
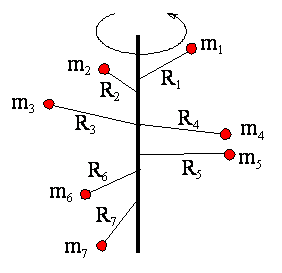
Proszę zwrócić uwagę, że R tutaj nie jest wektorem – jest najkrótszą odległością od osi obrotu.

Jeżeli masa m jest rozłożona w sposób ciągły w objętości V, to moment bezwładności ciała względem dowolnej osi (przechodzącej przez objętość ciała lub poza nią) obliczamy na podstawie ogólnego równania:
![]()
gdzie r jest odległością elementu masy dm od osi obrotu, ρ - lokalną gęstością ciała, zaś dV - objętością zajmowaną przez element masy dm.

W
ogólnym przypadku, całkowanie po całej objętości bryły w obliczaniu momentu
bezwładności może być bardzo trudne albo niewykonalne. Jeżeli jednak bryła jest
symetryczna względem osi, dla której obliczamy moment bezwładności, to
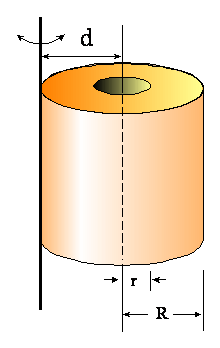
całkowanie może być całkiem łatwe. Przykładem może być wydrążony walec o masie
M i o promieniu wewnętrznym r, a zewnętrznym R:
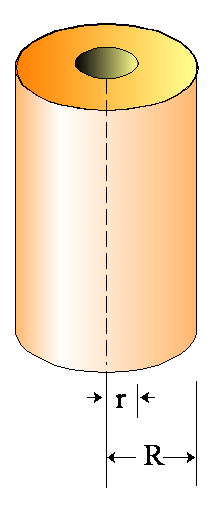
Jeżeli
moment bezwładności I liczymy względem osi walca, to standardowo dzielimy go na
nieskończenie cienkie cylindry o grubości dx i masie dm.

Moment bezwładności takiego
cienkiego cylindra wynosi dI = x2 dm. Dlaczego? Moment bezwładności
całego walca wyniesie
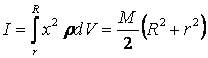
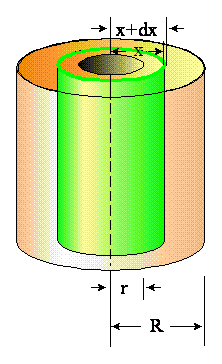
Dlaczego moment bezwładności nie znika, kiedy
R = r ?
Dlaczego moment bezwładności nie zależy od
długości walca ?
Inne przykłady obliczania momentów
bezwładności:
Przykład 2. Obliczanie momentu bezwładności I jednorodnej kuli o masie M i o promieniu R. Moment I liczymy względem osi przechodzącej przez środek kuli. Sposób pierwszy: Oś obrotu umieszczamy wzdłuż osi x z początkiem w środku kuli. Kulę dzielimy na cienkie dyski o zmiennych promieniach r ≤ R mających grubość dx i masę dm, jak na rys. a). Pomocniczo wyliczamy moment bezwładności elementarnego dysku względem osi obrotu przechodzącej przez jego środek i prostopadłej do jego powierzchni. Chwilowo założymy, że dysk ma masę m i promień r (rys. b). Dzielimy dysk na pierścienie o promieniach x.

Każdy pierścień o szerokości dx i masie dm będzie miał względem osi obrotu moment bezwładności dI = x2dm.
![]()
Ponieważ dm = σ dS, gdzie σ = m/S = m/(πr2) jest gęstością powierzchniową masy, a dS = 2πx dx jest powierzchnią pierścienia, to
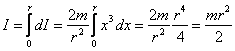
Stąd
![]()
Jeżeli ten wynik zastosujemy do rys. a), to poprzednio wyliczone I będzie spełniało rolę dI z masą dm
![]()
zaś
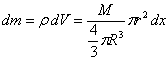
gdzie dV jest objętością dysku. Stąd
![]()
Ale
![]()
czyli
![]()
Obliczając I całkujemy to wyrażenie w granicach od 0 do R i aby uwzględnić obie półkule wynik mnożymy przez dwa:
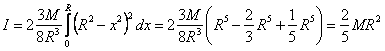
Ostatecznie, moment bezwładności kuli liczony względem jej osi jest równy
![]()
Sposób drugi: Kulę dzielimy na współosiowe cylindry o wysokościach h i promieniach x, jak na rys. c). Oś cylindrów jest także osią obrotu. Moment bezwładności każdego z cylindrów wynosi
![]()
gdzie
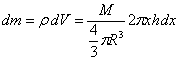
Ponieważ
![]()
to
![]()
Moment bezwładności kuli znajdujemy z całki
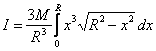
Całkujemy stosując podstawienie R2 - x2 = t2 i ponownie otrzymujemy
![]()
e) Sfera o promieniu R i o masie m. Moment bezwładności liczymy względem osi. Powierzchnię sfery tniemy na współosiowe pierścienie o promieniu x i szerokości dx, jak na rysunku poniżej:
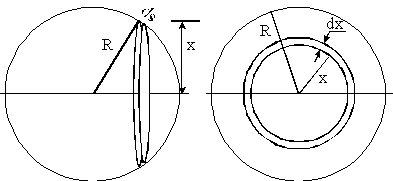
Moment bezwładności pojedynczego pierścienia dI wynosi
![]()
oraz
![]()
Wartość I znajdujemy przez całkowanie względem φ w granicach od 0 do π (stosujemy podstawienie cos φ = u; - sin φ dφ = du) i znajdujemy dla sfery
![]()
Ten wynik możemy zastosować w jeszcze jednej metodzie liczenia momentu bezwładności dla kuli o masie m i o promieniu R. Wewnątrz kuli wydzielamy sferę o promieniu x i o grubości ścianki dx. Moment bezwładności tej sfery na podstawie poprzedniego wyrażenia wynosi
![]()
Stąd ponownie znajdujemy moment bezwładności kuli
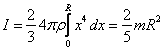
W przypadku figur płaskich wygodnym sposobem liczenia momentu bezwładności względem osi prostopadłej do tej figury jest następujące spostrzeżenie: Jeżeli początek układu odniesienia znajduje się na powierzchni figury i osie x oraz y leżą również na tej powierzchni, to moment bezwładności figury względem osi z prostopadłej do jej powierzchni jest sumą momentów bezwładności figury względem osi x i osi y
![]()
Uzasadnienie tego jest proste. Ponieważ
![]()
a r2 = x 2 + y 2, gdzie r jest odległością elementu masy od osi z, otrzymujemy wymienioną wyżej relację:
![]()

Całkowanie
byłoby często niezwykle trudne gdyby oś, względem której obliczamy I, nie była
osią symetrii, np. gdyby przechodziła na zewnątrz. Jeżeli ta nowa oś jest
równoległa do osi przechodzącej przez środek masy i jest od niej oddalona o
odległość d, to wtedy możemy zastosować twierdzenie o osiach równoległych (tzw.
twierdzenie Steinera):
Jeżeli moment bezwładności bryły o
masie M liczony względem osi przechodzącej przez jej środek masy wynosi I0,
to moment bezwładności I liczony względem innej osi równoległej do poprzedniej
i oddalonej od niej o d jest równy
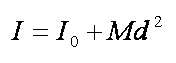
|
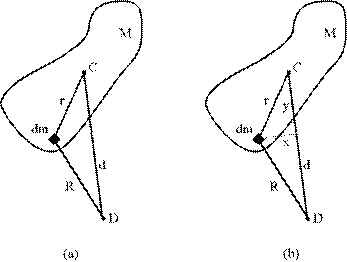
Dowód twierdzenia Steinera. Wybierzmy płaską płytkę o masie M (każdą bryłę trójwymiarową możemy pociąć na stos takich „talarków”). Oś obrotu przechodzi przez środek masy C i jest prostopadła do płaszczyzny płytki. Moment bezwładności płytki względem tej osi oznaczymy przez I0. Szukamy momentu bezwładności I względem osi przechodzącej przez punkt D i równoległej do osi przechodzącej przez środek masy (punkt C). Odległość między oboma osiami wynosi d. Sytuacja jest przedstawiona na rys. (a).
Wybieramy w otoczeniu dowolnego punktu na płytce element masy dm. Przy oznaczeniach, jak na rysunku, moment bezwładności I0 względem osi przechodzącej przez C wyniesie
Celem jest znalezienie momentu bezwładności I płytki względem osi przechodzącej przez D
Z elementu masy dm opuszczamy
odcinek normalny do prostej d, jak na rys. (b). W powstałym w ten sposób
trójkącie prostokątnym, w którym
Po pomnożeniu obu stron równania przez dm i po scałkowaniu po całej powierzchni płytki otrzymujemy
czyli
Należy zauważyć, że odległość y
jest mierzona od środka masy, a całka
i tym samym twierdzenie Steinera zostało udowodnione. |

W ruchu obrotowym bryły sztywnej jej kształt jest w zasadzie bez znaczenia, gdyż jej ruch jest określony przez jej osie bezwładności. Każdej bryle, niezależnie od tego, jak nieregularny jest jej kształt i niejednorodna gęstość, odpowiada elipsoida bezwładności. Na ogół, jest to elipsoida trójosiowa a jej osie noszą nazwę głównych osi bezwładności. Długość każdej z tych osi jest proporcjonalna do momentu bezwładności względem tej osi.
Głównymi osiami bezwładności (osiami elipsoidy będącej powierzchnią zdiagonalizowanego tensora bezwładności) nazywamy trzy osie przechodzące przez środek masy C i mające takie kierunki, że:
I - moment bezwładności względem tej osi jest największy;
II - prostopadła do osi I. i taka, względem której moment bezwładności ciała jest najmniejszy;
III - prostopadła do obu osi I. i II.
Momenty bezwładności określone względem głównych osi bezwładności noszą nazwę głównych momentów bezwładności II, III i IIII. Wartości głównych momentów bezwładności są równe długościom odpowiednich półosi elipsoidy bezwładności. Wartość momentu bezwładności Ix względem każdej innej osi przechodzącej przez środek masy C jest równa długości odcinka tej osi zawartego między środkiem masy a powierzchnią elipsoidy bezwładności. Oznacza to, że trzy główne momenty bezwładności określają momenty bezwładności względem wszystkich osi przechodzących przez środek masy.
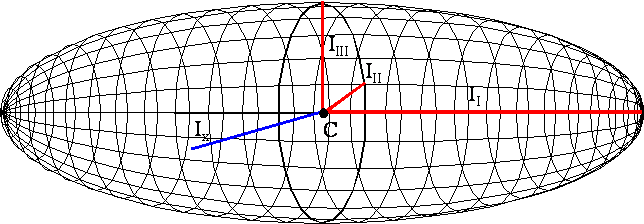
Obrót bryły sztywnej wokół dowolnej osi przechodzącej przez środek masy można zawsze rozłożyć na trzy równoczesne obroty wokół głównych osi bezwładności. Taki rozkład nie jest możliwy dla jakichkolwiek innych trzech osi prostopadłych względem siebie. Najprostszymi rodzajami ruchu bryły sztywnej jest ruch obrotowy względem jednej z głównych osi bezwładności. Ruch taki jest stabilny tylko wtedy, gdy odbywa się wokół osi, dla której moment bezwładności jest największy. Ruch wokół osi II., dla której moment bezwładności jest najmniejszy, jest także stabilny, ale wtedy najmniejsze zaburzenie ruchu powoduje, że pojawia się para sił odśrodkowych, która stara się doprowadzić do obrotu wokół osi I. ciała. Ruch wokół osi III. jest zawsze niestabilny.

Wyrażenie na energię kinetyczną
ruchu obrotowego otrzymujemy przez proste przekształcenie wyrażenia na energię
kinetyczną w ruchu liniowym. Zastosujemy związek między prędkościami liniową i
kątową oraz promieniem obrotu ![]() i otrzymujemy dla punktu materialnego
i otrzymujemy dla punktu materialnego
![]()
Stąd
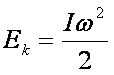
gdzie I jest
momentem bezwładności. Otrzymane wyrażenie na energię kinetyczną jest prawdziwe
również i dla bryły sztywnej. Oś obrotu bryły musi być tą samą osią względem
której obliczamy moment bezwładności.