KINEMATYKA
RUCHU OBROTOWEGO
Droga
kątowa, prędkość kątowa i przyśpieszenie kątowe.
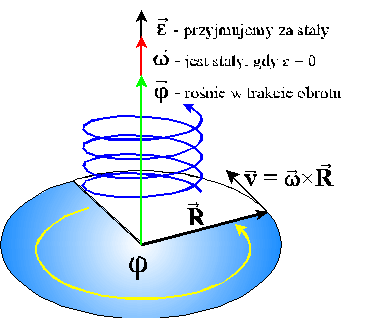
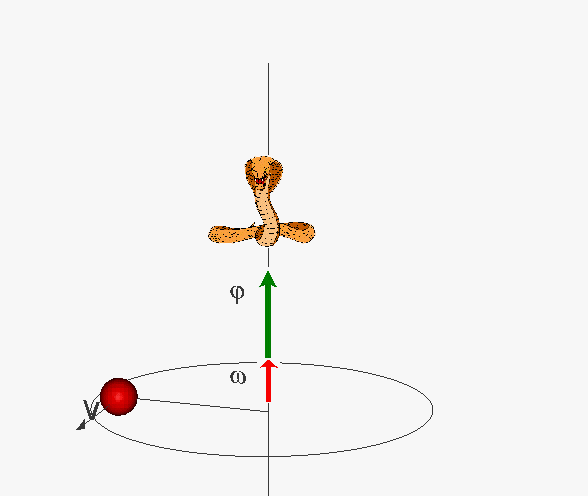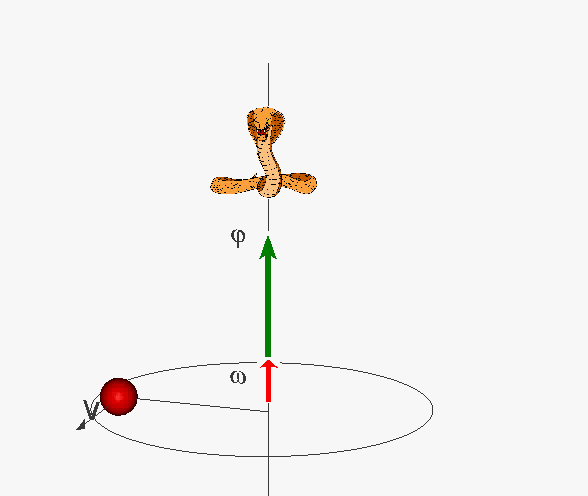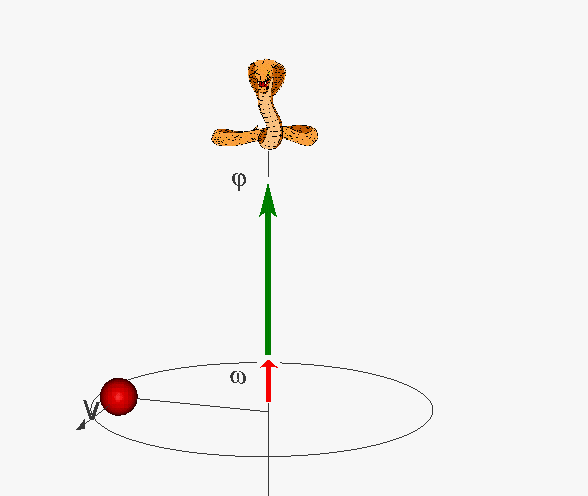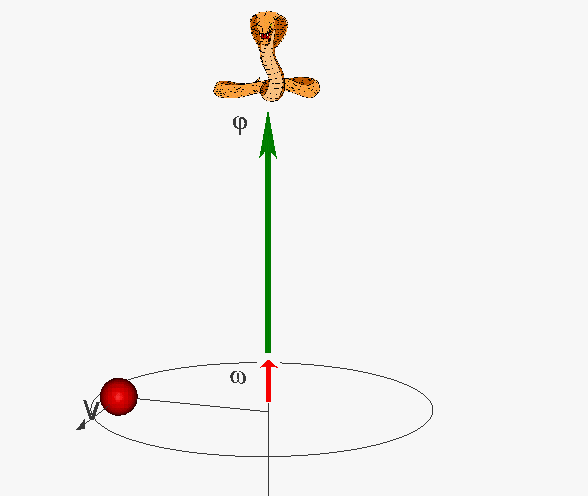
Kiedy ruch ciała zostanie ograniczony w ten sposób, że żaden punkt tego ciała nie będzie mógł się oddalić od pewnej osi, to ciało musi wtedy wykonywać ruch obrotowy wokół tej osi.
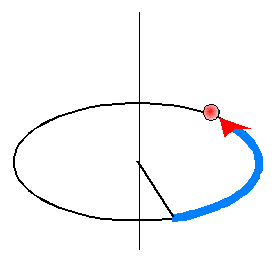
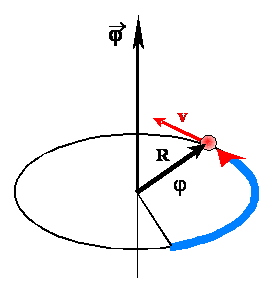
Zapamiętaj – łuk ze strzałką nie jest wektorem. Wektor ma tylko jeden kierunek. Tutaj łuk pokazuje tylko kierunek obrotu (wybrany jako dodatni matematycznie). Promień ruchu jest wektorem i oznaczymy go przez R. Ponieważ ciało ma prędkość liniową v, to po czasie t promień obróci się o kąt φ. Kąt φ nazywamy drogą kątową, której przypisujemy cechy wektora. Wektor kąta jest, zatem, wektorem leżącym na osi obrotu, mającym długość równą wartości liczbowej kąta obrotu i zwrot określony przez ruch śruby prawoskrętnej.
Gdy ruch obrotowy odbywa się po
torze o chwilowym promieniu krzywizny R, to po obrocie o kąt φ długość
łuku zakreślonego przez punkt materialny S wynosi
oraz w ogólnym przypadku (np., gdy promień R nie jest stały
w czasie obrotu)
Stąd prędkość liniowa punktu na torze krzywoliniowym
wyniesie
Ponieważ droga kątowa θ jest wektorem, to także prędkość kątową ω definiujemy jako wektor:
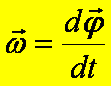
Podobnie
jak droga kątowa, również i prędkość kątowa jest wektorem leżącym na osi obrotu
a element drogi kątowej, jaki przebywa punkt w czasie dt wynosi:
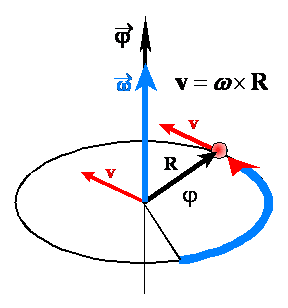
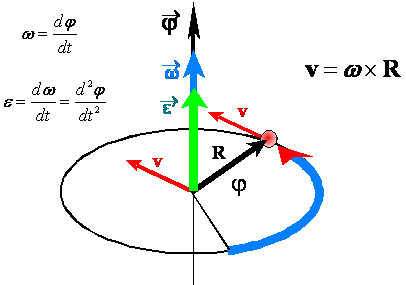
Kiedy wektory R i
ω są do siebie prostopadłe to
możemy napisać skalarny związek między prędkościami liniową v i kątową w: 
. Jednak najbardziej ogólny związek między
wektorami v, w i R jest wyrażony przez iloczyn wektorowy:
Jeżeli
punkt porusza się ze stałą prędkością kątową ω, to droga kątowa φ
rośnie jednostajnie:
Przyśpieszenie
kątowe ε definiujemy analogicznie, jak przyśpieszenie liniowe, czyli jako
prędkość zmian prędkości kątowej ω lub jako drugą pochodną drogi kątowej
względem czasu:
Wektor przyspieszenia kątowego
także leży na osi obrotu i jego zwrot określony przez ruch śruby prawoskrętnej.
W naszym kursie będziemy zawsze przyjmowali, że
przyśpieszenie kątowe jest stałe. Jeżeli przez φ0 i ω0
oznaczymy drogę początkową i prędkość początkową, odpowiednio, to drogę kątową φ jako funkcję czasu t możemy zapisać
następująco:
