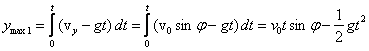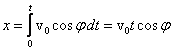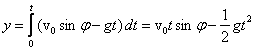Back to Index

PRAWO GRAWITACJI NEWTONA.

Natężenie pola grawitacyjnego, potencjał grawitacyjny.

Środek masy.

* Prawo grawitacji Newtona

* Natężenie pola grawitacyjnego

* Grawitacyjna energia potencjalna i potencjał grawitacyjny

* Prędkości kosmiczne

* Przykład ruchu ciała w polu grawitacyjnym: Rzut ukośny

* Środek masy układu punktów materialnych

* Środek masy brył materialnych

* Zastosowania twierdzeń Pappusa do obliczeń środka masy brył materialnych

* Porównanie oddziaływania grawitacyjnego z pozostałymi trzema fundamentalnymi oddziaływaniami w przyrodzie

* Grawitacja w kosmologii

Prawo grawitacji Newtona orzeka, że każde ciało we Wszechświecie przyciąga każde inne ciało siłą wprost proporcjonalną do iloczynu mas obu ciał, M i m, i odwrotnie proporcjonalnie do kwadratu odległości r między środkami masy obu ciał. Siła ta jest zawsze przyciągająca i działa wzdłuż prostej łączącej oba środki masy.

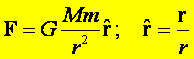
Współczynnik G jest uniwersalną stałą grawitacji o wartości

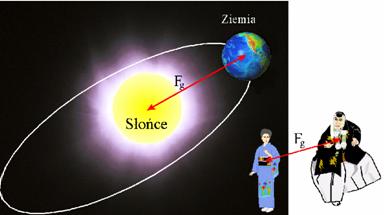
Siła grawitacji działa tak między ciałami niebieskimi o ogromnej masie, jak i między ciałami o masach znikomych w skali kosmicznej, chociaż w tym ostatnim przypadku jest ona niezauważalnie mała.

Natężeniem pola grawitacyjnego lub w skrócie polem grawitacyjnym nazywamy stosunek siły F działającej na ciało do masy m tego ciała umieszczonego w polu. Wartość i kierunek natężenia pola grawitacyjnego określa wektor g :

Natężenie pola grawitacyjnego g jest podstawowym parametrem charakteryzującym to pole. Siłę działającą na masę m w polu grawitacyjnym nazywamy potocznie ciężarem tego ciała w:

Kiedy określamy ciężar ciała znajdującego się w pobliżu Ziemi, to M będzie masą Ziemi, zaś r - odległością od środka masy ciała do środka Ziemi.

Drugim parametrem charakteryzującym pole grawitacyjne jest potencjał grawitacyjny charakteryzujący zdolność pola do nadawania energii potencjalnej ciału, jakie się w nim znajdzie. Potencjał grawitacyjny, oznaczany przez symbol γ, definiujemy jako stosunek energii potencjalnej U_g jaką ma (lub miałoby) ciało o masie m umieszczone w polu grawitacyjnym do wartości tej masy:

Znalezienie energii potencjalnej U_g nie jest tak proste jak określenie siły, którą można po prostu zmierzyć. Ponieważ jednak energia potencjalna ciała jest określona przez jego położenie (a nie przez jego ruch) to energię potencjalną ciała o masie m umieszczonego w pewnym punkcie znajdziemy przez obliczenie pracy, jaką należy wykonać, aby przenieść ciało z tego właśnie punktu do nieskończoności gdzie siła grawitacji już znika.

Przypuśćmy, że obliczamy energię potencjalną jaką ma masa m znajdująca się w odległości R od środka innej masy M. (Fo5e.wpg)

W tym celu obliczamy pracę, jaką wykona pole grawitacyjne w czasie przenoszenia tej masy m od R do nieskończoności. Wybieramy dowolne położenie chwilowe masy m w odległości r i z tego punktu przesuwamy ją o odległość dr. Sile grawitacji F i przesunięciu dr nadajemy cechy wektorowe, jak na rysunku. Praca wykonana przez pole grawitacyjne na odcinku dr wyniesie

Praca ta jest ujemna, ponieważ wektory F i dr są przeciwnie skierowane (my, oczywiście, wykonamy pracę dodatnią, bo siła wywierana przez nas jest równoległa do przesunięcia, ale przecież opisujemy pole grawitacyjne i masy, a nie samych siebie). Praca wykonana przez pole grawitacyjne na drodze z punktu R do nieskończoności będzie określona przez całkę

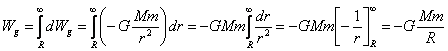
Grawitacyjna energia potencjalna U_g jest równa pracy W_g wykonanej przez pole, czyli

Ostatecznie potencjał grawitacyjny możemy zapisać w postaci

Na podstawie wyrażenia możemy napisać interesujący związek między siłą grawitacji działającą na ciało, a spadkiem (gradientem) potencjalnej energii grawitacji tego ciała:

Pierwszą prędkością kosmiczną nazywamy taką minimalną prędkość, jaką musi posiadać ciało o masie m, aby mogło poruszać się wokół Ziemi po stabilnej orbicie o promieniu r. Na takiej orbicie wystąpi równowaga dośrodkowej siły grawitacji i odśrodkowej siły bezwładności

Stąd, dla orbity znajdującej się na wysokości h nad Ziemią mającą promień R, pierwsza prędkość kosmiczna wynosi

Druga prędkość kosmiczna (prędkość ucieczki) to taka minimalna prędkość, jaka umożliwia ciału o masie m osiągnięcie nieskończonej odległości od Ziemi. Energia kinetyczna, jakiej w tym celu należy nadać ciału, musi być równa energii potencjalnej ciała na powierzchni Ziemi. Dlatego

Stąd druga prędkość kosmiczna wynosi

Analogicznie definiujemy obie prędkości kosmiczne dla dowolnego innego ciała niebieskiego.

Przykład ruchu ciała w polu grawitacyjnym: Rzut ukośny

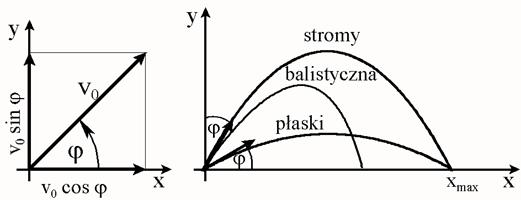
Nadanie ciału o masie m prędkości początkowej v₀ skierowanej pod kątem φ oznacza, że to ciało będzie miało jednocześnie poziomą prędkość początkową v₀ cos φ i pionową prędkość początkową v₀ sin φ, jak to pokazano na lewym rysunku.

Analizując ruch ciała w rzucie ukośnym przyjmujemy następujące założenia:

1. Przyśpieszenie grawitacyjne g (wartość wektora natężenia pola grawitacyjnego g) jest stałe na całym torze ciała a zatem prędkość w kierunku pionowym v_y podlega ciągłym zmianom i po czasie t wynosi ;

2. Pomijamy opór powietrza a zatem prędkość ciała w kierunku poziomym vx jest stała a ciało leci w tym kierunku tak długo jak długo znajduje się w powietrzu.

W punkcie, w którym ciało osiąga maksymalna wysokość, jego prędkość wynosi zero

.

Na tej podstawie otrzymujemy czas lotu ciała t od miejsca jego wyrzucenia do osiągnięcia najwyższego wzniesienia

Czas spadania ciała z maksymalnej wysokości do miejsca startu jest taki sam jak i czas jego wznoszenia. Oznacza to, że czas przebywania ciała w powietrzu a zatem i czas jego lotu w kierunku poziomym wynosi

Przez proste pomnożenie stałej prędkości poziomej przez czas przebywania ciała w powietrzu otrzymujemy zasięg rzutu pod kątem x_max:

Ponieważ , to zasięg maksymalny wynosi

Interesujący wynik dostaniemy po zastosowaniu własności funkcji sinus: . Po uwzględnieniu tej własności symetrii znajdujemy, że zasięg maksymalny wyraża się również wzorem

czyli, że

Zasięgi x_max przy strzelaniu po torze płaskim i torze stromym są jednakowe ale ponieważ w obu tych przypadkach składowe pionowe prędkości są różne, v_o sin φ oraz v₀ sin(90º - φ), to i wysokości maksymalne y_max ciała będą w obu przypadkach różne. Wysokość maksymalną dla toru płaskiego y_max1 otrzymamy przez proste całkowanie

Podstawiając czas wznoszenia się ciała

otrzymujemy

Analogicznie dla toru stromego otrzymujemy

Stosunek obu wysokości maksymalnych wyniesie

Dla φ = 45º obie te wysokości stają się, oczywiście, jednakowe.

Na koniec znajdziemy równanie toru ciała w rzucie pod kątem. Najpierw wyznaczymy współrzędne x i y ciała w funkcji czasu. Ponieważ

oraz

to po prostym całkowaniu znajdujemy

oraz

Standardowe postępowanie przy znajdowaniu toru ciała polega na wyeliminowaniu czasu z tych równań. Z pierwszego równania mamy

Po podstawieniu tego wyrażenia do drugiego z równań i po prostym przekształceniu znajdujemy, że tor ciała jest opisywany przez równanie

Jest to równanie odwróconej paraboli, jak pokazane na prawym rysunku.

Rzeczywistym torem pocisku jest tzw. krzywa balistyczna, której kształt zależy od wielkości oporów stawianych przez powietrze, czyli od ciśnienia, wilgotności i wiatru oraz od kształtu samego pocisku. Zasięg krzywej balistycznej jest znacznie mniejszy od zasięgu określonego przez idealny tor paraboliczny.

ŚRODEK MASY UKŁADU PUNKTÓW MATERIALNYCH I BRYŁ MATERIALNYCH

Środkiem masy układu połączonych ze sobą punktów materialnych (punktów mających masę) lub brył materialnych jest taki punkt, w którym pozornie zgromadzona została cała masa układu. Podparcie lub podwieszenie układu w tym punkcie nie powoduje zmiany położenia tego układu w przestrzeni. Układ pozostanie wtedy w równowadze, choćby chwiejnej (czyli takiej, kiedy po wychyleniu układ już nie wraca do położenia równowagi).

Kiedy zawiesimy na belce kilka przedmiotów to środek masy układu będzie takim punktem w którym podparcie nie spowoduje obrotu tego układu.

Położenie środka masy znajdziemy przyporządkowując każdemu punktowi podwieszenia pewną współrzędną, np. x

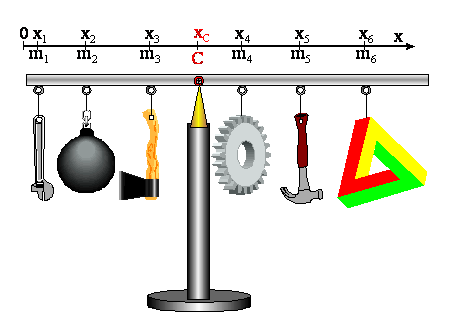
Współrzędna środka masy będzie średnią ważoną:

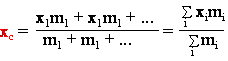
Postąpimy bardziej elegancko, kiedy rysowanie przedmiotów zastąpimy w sposób ogólny przez punkty, które je będą reprezentowały

Teraz środek masy C będzie wyróżnionym punktem którego współrzędna x_c będzie, oczywiście, średnią ważoną jak określona wyżej.

Kiedy nasze punkty nie leżą na osi, ale są rozrzucone na płaszczyźnie,

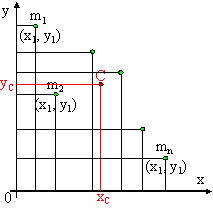
wtedy płaszczyznę możemy określić jako xy i nadać punktom odpowiednie współrzędne. Współrzędną środka masy x_c znajdziemy rzutując wszystkie punkty na oś x (zmieniając tylko współrzędne y, bez zmiany współrzędnych x)

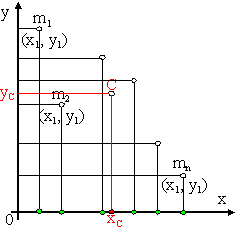
Wartość współrzędnej środka masy x_c otrzymujemy również jako średnią ważoną:

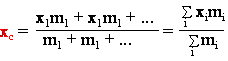
Współrzędną środka masy y_c znajdujemy analogicznie rzutując wszystkie punkty na oś y (zmieniając tylko współrzędne x, bez zmiany współrzędnych y)

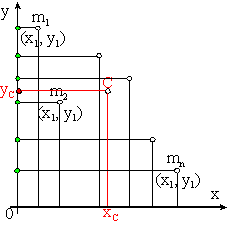
Wartość współrzędnej y_c otrzymujemy analogicznie jako średnią ważoną:

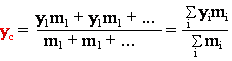
W przypadku przestrzennego rozłożenia punktów materialnych o masach m_n i współrzędnych (x_n, y_n, z_n) wartości współrzędnych środka masy (x_C, y_C, z_C) znajdujemy stosując ten sam schemat, jak dla jednego i dwóch wymiarów:

- dla x_C: rzutujemy wszystkie punkty na oś x (zmieniając współrzędne y i z)

- dla y_C: rzutujemy wszystkie punkty na oś y (zmieniając współrzędne x i z)

- dla z_C: rzutujemy wszystkie punkty na oś z (zmieniając współrzędne x i y)

Wartość współrzędnej z_c otrzymujemy analogicznie jak poprzednio

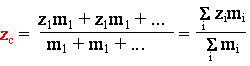
Szukając środka masy C bryły o masie M zanurzamy bryłę w układzie odniesienia x, y, z i wycinamy w niej element objętości dV = dx dy dz, który odpowiada elementowi masy dm = ρdV, gdzie ρ jest gęstością bryły

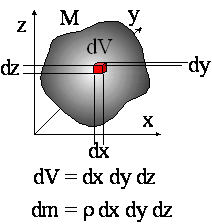
Z elementami masy dm postępujemy zupełnie podobnie, jak przedtem z masami m_i. Ponieważ jednak masy dm są nieskończenie małe, to sumowanie we wzorach na współrzędne środka masy musimy zastąpić całkowaniem. Całkowanie prowadzi się po całej objętości bryły. W rezultacie otrzymujemy wyrażenia zupełnie analogiczne:

Dla układu punktów Dla brył

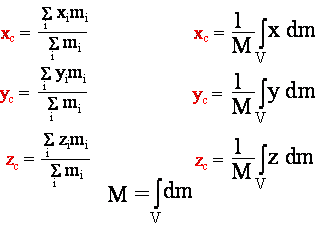
PRZYKŁADY OBLICZEŃ ŚRODKA MASY BRYŁ MATERIALNYCH

Przyklad 1: Znaleźć środek masy jednorodnego pręta o masie M i o długości L (Fo8a.wpg).

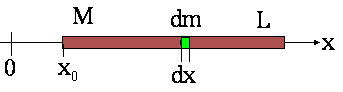
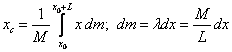
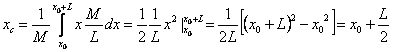
Przykład 2: Znaleźć środek masy jednorodnej płyty mającej kształt trójkąta równoramiennego. Płyta ma masę M, długość podstawy A i wysokość H (Fo8c.wpg).

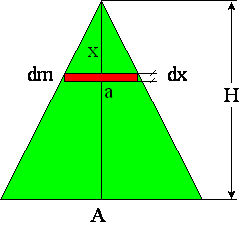
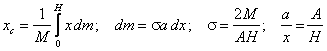
Przykład 3: Znaleźć środek masy jednorodnego stożka obrotowego o promieniu podstawy R i o wysokości H (Fo8d.wpg).

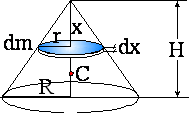
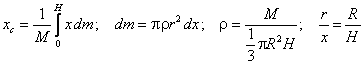
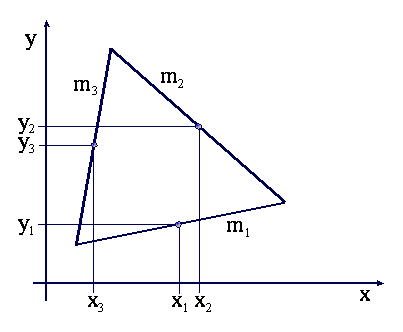
Niekiedy zagadnienie znalezienia środka masy złożonej bryły można sprowadzić do problemu środka masy układu punktów materialnych, jak np. dla krzywej łamanej utworzonej z pręta (Fo8bb.wpg):

ZASTOSOWANIA TWIERDZEŃ PAPPUSA DO OBLICZEŃ ŚRODKA MASY BRYŁ MATERIALNYCH

W znajdowaniu środka masy bryły materialnej użyteczne są dwa twierdzenia Pappusa.

1. Twierdzenie o polu powierzchni: Jeżeli krzywą płaską o długości L obrócimy o pewien kąt dookoła dowolnej osi leżącej w tej samej płaszczyźnie i nie przecinającej tej krzywej, to pole tak powstałego płata powierzchni obrotowej jest równe iloczynowi długości L i długości drogi S jaką przebył środek masy C tej krzywej.

2. Twierdzenie o objętości: Jeżeli zamkniętą figurę płaską o polu A obrócimy o pewien kąt dookoła dowolnej osi leżącej w tej samej płaszczyźnie i nie przecinającej tej figury, to objętość tak powstałej bryły obrotowej jest równa iloczynowi pola A i długości drogi S jaką przebył środek masy C tej figury.

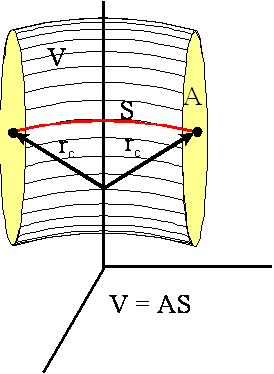
Drugie twierdzenie jest to oczywiście słuszne, gdy przesuwamy rozważaną figurę wzdłuż prostej prostopadłej do niej, lecz gdy przesuwamy ją po okręgu lub innej krzywej, mogą powstać dość szczególne bryły. Jednak dla toru zakrzywionego część zewnętrzna przesuwa się bardziej a część wewnętrzna mniej i oba efekty równoważą się. Jeśli więc chcemy znaleźć położenie środka masy płaskiego płata o stałej gęstości, wystarczy pamiętać, że objętość powstająca przez jego obrót wokół osi równa się odległości, którą zatoczył środek masy, mnożonej przez powierzchnię płata.

Ponieważ naszym zadaniem jest znajdowanie środków masy, to w twierdzeniach Pappusa tak wybieramy osie obrotów i kąty, o jakie obracamy łuki lub płaty powierzchniowe, aby łatwo było znaleźć odpowiednie pola powierzchni i objętości brył, jakie powstają w rezultacie obrotów.

Jeśli chcemy na przykład znaleźć położenie środka masy trójkąta prostokątnego o podstawie D i wysokości H, możemy problem ten rozwiązać w następujący sposób. Wyobrażamy sobie oś przechodzącą przez H i obracamy trójkąt wokół tej osi o pełne 360^o. Powstaje w ten sposób stożek. Odległość, którą przebył środek masy o współrzędnej x_c, wynosi 2πx_c. Przesuwaną figurą był trójkąt; jego pole równa się 1/2 HD. Odległość, jaką przebył środek masy, mnożona przez pole trójkąta, równa się objętości powstałej figury, która wynosi oczywiście πD²H/3. Zatem (2πx_c)(1/2 HD)= 1/3πD²H, czyli x_c = D/3. W podobny sposób, dokonując obrotu wokół innej osi lub powołując się na symetrię, znajdujemy, że y_c = H/3. Istotnie, środek masy każdej jednorodnej powierzchni trójkąta znajduje się w punkcie, w którym trzy środkowe - linie poprowadzone z wierzchołków do środków przeciwległych boków - przecinają się (punkt ten znajduje się w 1/3 drogi wzdłuż każdej środkowej). Aby się o tym przekonać, podzielmy trójkąt na wiele małych warstw równoległych do podstawy. Należy zauważyć, że środkowa dzieli na połowę każdą z tych warstw, a więc środek masy musi na niej leżeć.

Bardziej złożonym przypadkiem jest znalezienie położenie środka masy jednorodnego półkola. Dla pełnego koła środek masy jest oczywiście w środku koła, lecz dla półkola problem jest trudniejszy. Niech r będzie promieniem półkola, a x_c odległością środka masy od prostej krawędzi. Jeśli półkole obrócimy wokół tej krawędzi tak, aby powstała kula, środek masy przebędzie odległość 2πx_c; powierzchnia wynosi πr²/2 (gdyż jest to tylko połowa koła). Powstająca objętość równa się oczywiście 4π r³/3; znajdujemy stąd, że

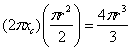
czyli

PORÓWNANIE ODDZIAŁYWANIA GRAWITACYJNEGO Z POZOSTAŁYMI TRZEMA FUNDAMENTALNYMI ODDZIAŁYWANIAMI W PRZYRODZIE.

Podstawowe oddziaływania w przyrodzie. Wszystkie znane oddziaływania, jakie wywierają na siebie ciała dzielimy na cztery rodzaje:

- oddziaływania grawitacyjne

- oddziaływania słabe

- oddziaływania elektromagnetyczne

- oddziaływania silne

Każde z tych oddziaływań bardzo znacznie różni się od pozostałych siłą, jaką ono wytwarza między dwoma ciałami. Tabela przedstawia względną siłę każdego z oddziaływań F względem siły oddziaływania elektromagnetycznego F_E.

Rodzaj oddziaływania	F / FE
Grawitacyjne	10^-40
Słabe	10^-10
Elektromagnetyczne	1
Silne	10^2

Przedstawiona lista zawiera wszystkie siły znane w przyrodzie i każde oddziaływanie między ciałami jest wytworzone przez jedną z tych czterech sił lub przez kombinację kilku z nich (np. w jednoczesnym działaniu siły grawitacji i sił elektromagnetycznych).

Najsłabszym z tych oddziaływań jest oddziaływanie grawitacyjne, w przybliżeniu słabsze od elektromagnetycznego 10⁴⁰ razy. Siła grawitacji wytworzona w tym oddziaływaniu jest zawsze przyciągająca i działa między ciałami posiadającymi masę. Wartość siły grawitacji opisuje znane nam już prawo grawitacji Newtona (siła ta jest wprost proporcjonalna do iloczynu obu działających mas i odwrotnie proporcjonalna do kwadratu odległości miedzy ich środkami masy).

Oddziaływanie słabe, w przybliżeniu słabsze od elektromagnetycznego 10¹⁰ razy, występuje między leptonami (np. elektronami, mionami (cząstkami μ) i taonami (cząstkami τ)) a także jest odpowiedzialne za rozpad β cząstek i jąder.

Oddziaływanie elektromagnetyczne tworzy siły odpowiedzialne za strukturę atomu, za reakcje chemiczne i za wszystkie zjawiska elektromagnetyczne w otaczającym nas świecie. Siły te działają tylko między naładowanymi cząstkami i mogą być zarówno przyciągające jak i odpychające, co odróżnia je od zawsze przyciągającej siły grawitacji. Wartość siły wytwarzanej w oddziaływaniu elektromagnetycznym między dwoma spoczywającymi ładunkami punktowymi opisuje tzw. siła Coulomba (siła ta jest wprost proporcjonalna do iloczynu obu działających ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi).

Oddziaływanie silne, w przybliżeniu 10²⁰ razy silniejsze od elektromagnetycznego, działa jedynie między cząstkami ciężkimi zwanymi hadronami, które dzielą się na bariony (np. proton, neutron) i mezony (np. mezon π). Jak zobaczymy dalej przy omawianiu Modelu Standardowego, hadrony mają strukturę wewnętrzną i składają się z kwarków, które uważamy za cząstki rzeczywiście elementarne. Każdy barion składa się z trzech kwarków, a mezon z jednego kwarka i jednego antykwarka. Oddziaływanie silne między nukleonami (proton, neutron) powoduje ich wzajemne związanie prowadzące do utworzenia jądra atomowego. Oddziaływania silne działające w jądrach atomowych mają bardzo krótki zasięg rzędu 10^-15 m.

GRAWITACJA W KOSMOLOGII: ZASADNICZE ZNACZENIE GRAWITACJI W EWOLUCJI GWIAZD I W ZACHOWANIU SIĘ DUŻYCH ZBIOROWISK GWIAZD.

Chociaż w skali atomowej siła grawitacji jest zaniedbywalnie mała, to kiedy działa w skali kosmicznej wewnątrz ciał o ogromnej masie (galaktyki, gwiazdy, planety) określa wzajemne ruchy tych ciał a jednocześnie jest bardzo ważnym czynnikiem w przebiegu ich ewolucji. W pewnych procesach ewolucji zachodzących w bardzo masywnych gwiazdach oddziaływania grawitacyjne generują wybuchy, których moc przewyższa wielokrotnie moce wytwarzane w reakcjach termojądrowych w tych gwiazdach.

Ewolucją gwiazdy nazywamy ciąg procesów, które przebiegają w gwieździe od jej narodzin aż do końcowego wygaszenia. Przyjmujemy, że gwiazda powstaje w wyniku kondensacji materii międzygwiezdnej, która zachodzi albo przypadkowo albo w wyniku niewyjaśnionych powodów. Gwiazda następnie rośnie w rezultacie grawitacyjnego przyciągania do siebie nowych mas materii. W tej pierwotnej chmurze zimnej ściskanej grawitacyjnie materii, zwanej protogwiazdą, pojawia się coraz większe ciśnienie wewnętrzne. Ten wzrost ciśnienia podnosi ciągle temperaturę aż do poziomu 5-10 × 10⁶ K i w tej temperaturze rozpoczyna się termojądrowe łączenie się wodoru z wytworzeniem helu. Okres tworzenia się protogwiazdy wynosi prawdopodobnie ok. 50 milionów lat. Po rozpoczęciu się reakcji termojądrowej ściskanie grawitacyjne jest równoważone przez wzrost ciśnienia wewnętrznego wywołanego przez tę reakcję.

W typowej gwieździe, jaką jest nasze Słońce, tempo spalania wodoru jest oceniane na ok. 10¹¹ kg s^-1, przy czym uwalnianie energii następuje z mocą ok. 6 × 10²⁵ J s^-1. Ocenia się, że Słońce zawierało wystarczającą ilość wodoru, aby spalać go w tym tempie przez 10¹⁰ lat i że Słońce znajduje się w połowie swego życia jako gwiazda. W końcu jednak okres stabilności gwiazdy dobiega końca, ponieważ energia wytwarzana w reakcjach termojądrowych w jej wnętrzu już dalej nie wystarcza do zrównoważenia ściskania grawitacyjnego. Jądro gwiazdy, zawierające teraz głównie hel, zapada się grawitacyjnie aż do momentu, w którym temperatura wzrośnie tak wysoko, aby w otaczającej jądro powłoce, złożonej z niespalonego dotąd wodoru, została zapoczątkowana nowa faza reakcji termojądrowych. Energia wytworzona w tych reakcjach powoduje, że powłoka zewnętrzna gwiazdy gwałtownie rozszerza się i oziębia. W tak obniżonej temperaturze barwa rozdętej teraz powłoki zmienia się z białej na czerwoną. Gwiazda, która znajduje się w tym stanie to czerwony olbrzym. Jednocześnie jądro gwiazdy jest ściskane grawitacyjnie osiągając temperaturę 10⁸ K i w tej temperaturze hel tworzący jądro staje się ośrodkiem, w którym wybuchają reakcje termojądrowe nowego rodzaju. Produktem tych reakcji jest węgiel. Gwiazdy o stosunkowo niewielkiej masie szybko spalają zawarty w jądrze hel i wtedy jądro ponownie zapada się grawitacyjnie tworząc obiekt, który nazywamy białym karłem. Powłoka zewnętrzna, która wcześniej należała do czerwonego olbrzyma, ucieka w tym czasie w przestrzeń kosmiczną.

Większe gwiazdy, wielokrotnie większe niż Słońce, mają w jądrze wystarczająco dużo helu na to, aby proces spalania był kontynuowany i wtedy powstają cięższe pierwiastki aż do żelaza włącznie. Zatem żelazo jest najcięższym pierwiastkiem, jaki może być wytworzony w procesach spalania helu w jądrze gwiazdy. Kiedy w tak dużej gwieździe hel zostanie w końcu wypalony wtedy wydarza się prawdziwa katastrofa na skalę kosmiczną. Cała ogromna masa gwiazdy zapada się grawitacyjnie a wytworzona w tym procesie energia powoduje gigantyczny wybuch całej gwiazdy. Zjawisko to nazywamy wybuchem supernowej. Moc energii promieniowania uwalnianego w wybuchu supernowej powoduje, że gwiazda promieniuje 10¹⁰ razy silniej niż przeciętna gwiazda. Oznacza to, że supernowa dominuje jasnością nad całą galaktyką, w której się ona znajduje. W wybuchu supernowej tworzą się już najcięższe pierwiastki występujące w przyrodzie. Czas życia supernowej jest jednak krótki i jej promieniowanie zanika już po kilku latach. Pozostałości po wybuchu supernowej kończą proces ewolucji tworząc tzw. gwiazdy neutronowe lub czarne dziury.

Gwiazda neutronowa jest gwiazdą, która osiągnęła kres swej drogi ewolucyjnej i w której brak już paliwa jądrowego. Nic teraz nie przeciwdziała maksymalnemu kolapsowi grawitacyjnemu i w jego rezultacie gwiazda staje się tak ściśnięta, że elektrony znajdujące się w jej wnętrzu zostają zmuszone do wejścia do jąder atomowych gdzie łącząc się z protonami zamieniają je w neutrony. Zgodnie z przyjętym modelem, gwiazda neutronowa ma gazową otoczkę o grubości kilku metrów, poniżej której znajduje się stała skorupa o grubości ok. 1 km. Pod skorupą rozciąga się nadciekła warstwa złożona prawie wyłącznie z neutronów. Samo centrum takiej gwiazdy stanowi ogromnie twardy rdzeń. Gwiazda neutronowa ma średnicę prawdopodobnie nie większą niż 10 km, ale jej masa jest 1.5 razy większa od masy Słońca czyli wynosi 3 × 10³⁰ kg. Oznacza to, że średnia gęstość gwiazdy neutronowej jest ok. 10¹⁵ razy większa od gęstości wody; jest to gęstość jakiej nie można spotkać nigdzie indziej we Wszechświecie. Przypuszcza się, że pulsary – niezwykle regularne zegary kosmiczne – są szybko rotującymi gwiazdami neutronowymi posiadającymi bardzo silne pola magnetyczne.

Czarna dziura jest obiektem w przestrzeni kosmicznej utworzonym także przez kolaps grawitacyjny, ale w tym przypadku obiekt jest tak masywny, że dla niego prędkość ucieczki (druga prędkość kosmiczna) jest równa prędkości światła. Przypuszcza się, że powstanie czarnej dziury bierze swój początek w wybuchu supernowej, w której pozostały po wybuchu rdzeń materii jest bardzo duży (wiele mas Słońca). Materia rdzenia jest poddana ogromnemu ściskaniu grawitacyjnemu, co prowadzi do dalszego wzrostu natężenia pola grawitacyjnego. W pewnym momencie to pole osiąga wartość krytyczną, czyli staje się tak duże, że promieniowanie elektromagnetyczne zostaje w nim uwięzione i nie może już rozchodzić się w przestrzeń kosmiczną. Wtedy tak utworzony obiekt już nie świeci, czyli staje się czarną dziurą. Powierzchnia, na której pole grawitacyjne osiąga tę wartość krytyczną nosi nazwę horyzontu zdarzeń. Nie możemy i nie będziemy nigdy mogli zarejestrować ani wykryć niczego, co wydarza się poniżej horyzontu zdarzeń. O istnieniu czarnych dziur wnioskujemy na podstawie obserwacji zachowania się ciał niebieskich znajdujących się w pobliżu tych dziur. Jeżeli, na przykład, czarna dziura tworzy układ podwójny ze zwykłą gwiazdą wtedy czarna dziura wysysa materię z tej gwiazdy. Wysysana materia tworzy najpierw dysk rotujący wokół czarnej dziury. Materia w dysku staje się skompresowana i podgrzana do tego stopnia, że emituje promieniowanie rentgenowskie.

10¹¹, CZYLI STO MILIARDÓW

Pole grawitacyjne wpływa na zachowanie się ogromnych zbiorowisk gwiazd, jakimi są galaktyki. Każda galaktyka – eliptyczna, spiralna lub nieregularna – zawiera ok. 10¹¹ gwiazd i wszystkie one utrzymywane są razem grawitacyjnie. Galaktyka, w której leży nasz Układ Słoneczny nosi nazwę Drogi Mlecznej i jest galaktyką spiralną a Słońce znajduje się na peryferiach tej spirali. Przypuszcza się, że w zasięgu największych teleskopów znajdują się pozostałe galaktyki, których liczbę we Wszechświecie ocenia się również na 10¹¹. Pole grawitacyjne ma również istotny wpływ na przebieg tak gigantycznych wydarzeń, jakimi są zderzenia galaktyk.

Przy okazji – liczba neuronów (komórek nerwowych) w naszym mózgu wynosi całkiem przypadkowo również 10¹¹. Każdy z tych neuronów kontaktuje się z komórkami receptorowymi, mięśniowymi, gruczołowymi lub z innymi neuronami siecią połączeń synaptycznych, których liczba może dochodzić do kilkuset na każdy neuron. Fantastyczna maszyna!

Back to Index