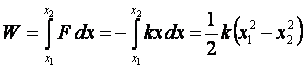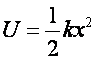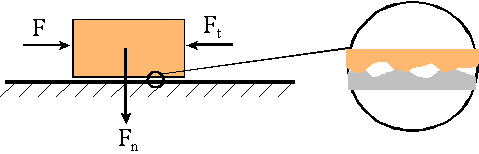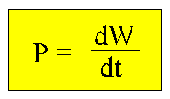Back to Index

PRACA W RUCHU LINIOWYM. SIŁY TARCIA. MOC

* Praca w ruchu liniowym

* Siły tarcia

* Moc

PRACA WYKONANA PRZEZ DOWOLNĄ SIŁĘ

W prostym przypadku, gdy siła F jest stała a droga s, na której ta siła działa, jest linią prostą wtedy pracę wykonaną przez siłę wyrażamy przez równanie:

Jeżeli jednak siła wykonująca pracę zmienia się w czasie i/lub w przestrzeni, a tor s, na którym praca jest wykonywana jest krzywoliniowy, to pracę obliczamy przez pocięcie toru na nieskończenie krótkie odcinki dl. Aby uwzględnić zmianę kierunku drogi (toru), odcinkowi dl nadajemy cechy wektorowe dl.

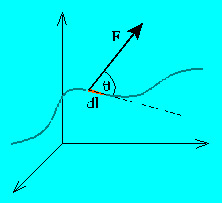
Praca wykonana przez dowolną siłę, stałą lub zmienną w czasie, działającą na drodze dl wynosi:

Jest to wyrażenie ścisłe, słuszne w każdej sytuacji bez żadnych ograniczeń. W przypadku kiedy droga, na której jest wykonywana praca, ma dowolny kształt i siła zmienia się w dowolny sposób, a pracę mamy obliczyć między dwoma dowolnymi punktami a i b drogi, to przedział między punktami a i b dzielimy na nieskończenie krótkie odcinki dl i przyjmujemy, że wektor siły F działającej na każdym z odcinków jest stały. Siła działająca na drodze makroskopowej między punktami a i b wykonuje pracę W, która jest wyrażona przez całkę

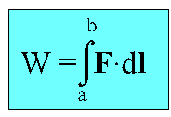
Obliczając pracę wykonaną między punktami a i b sumujemy prace F•dl wykonane na poszczególnych odcinkach

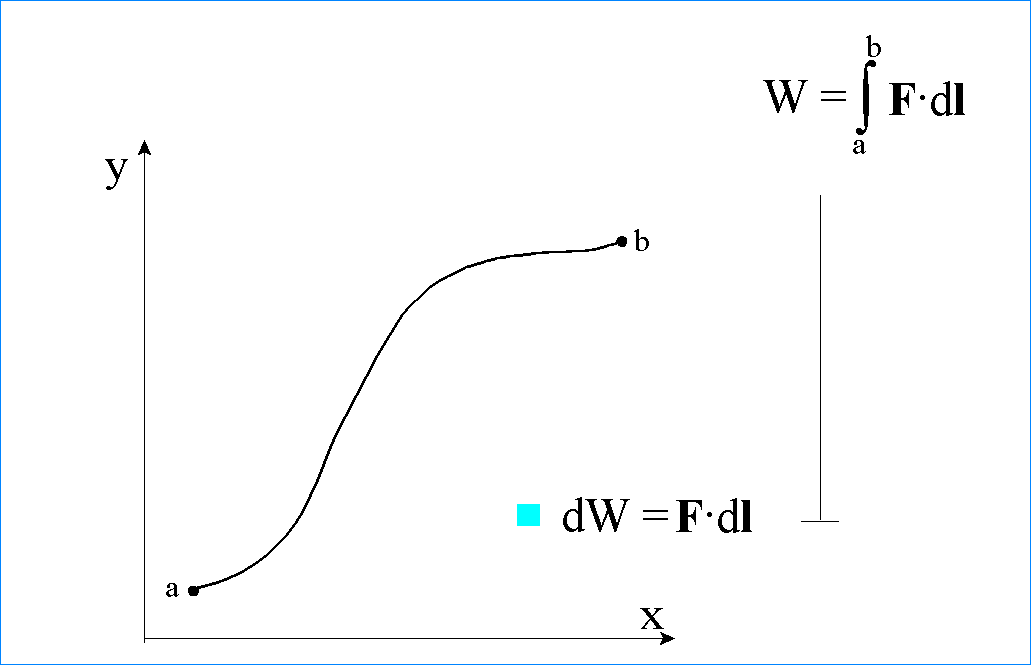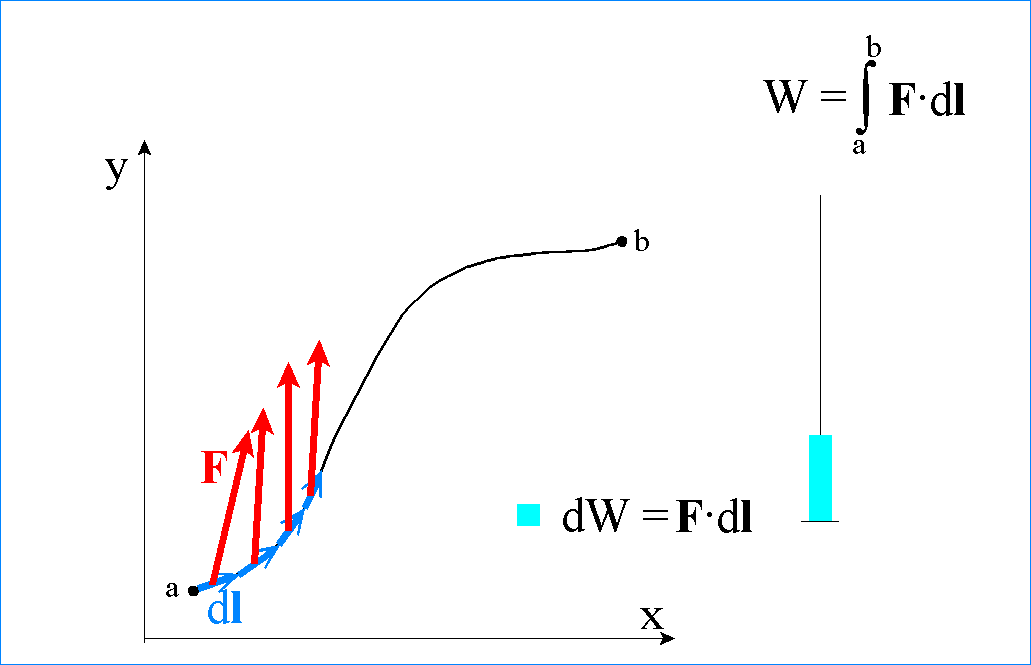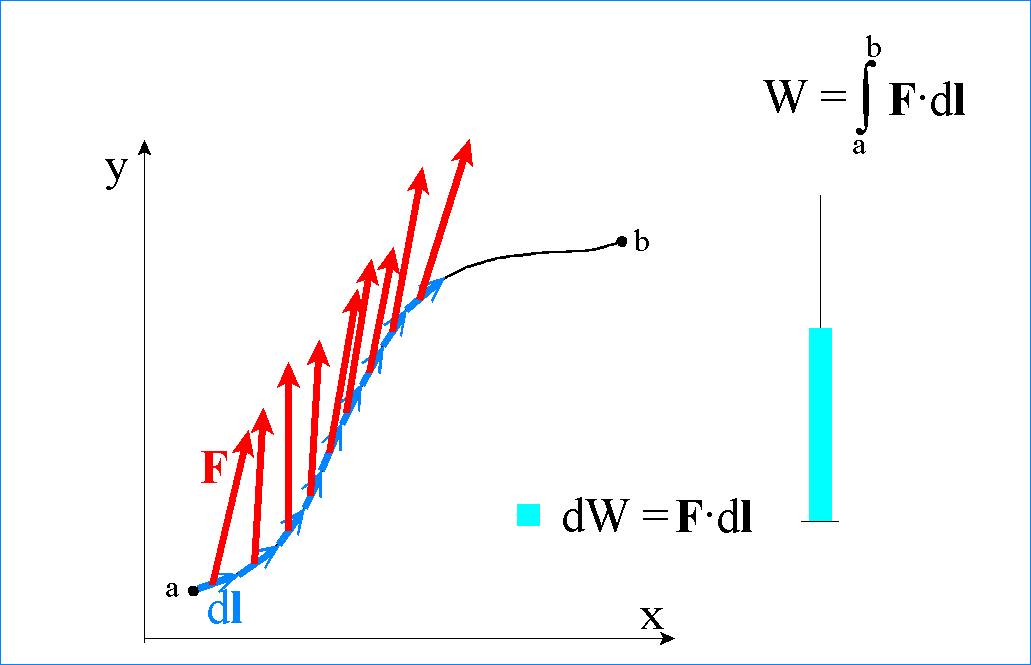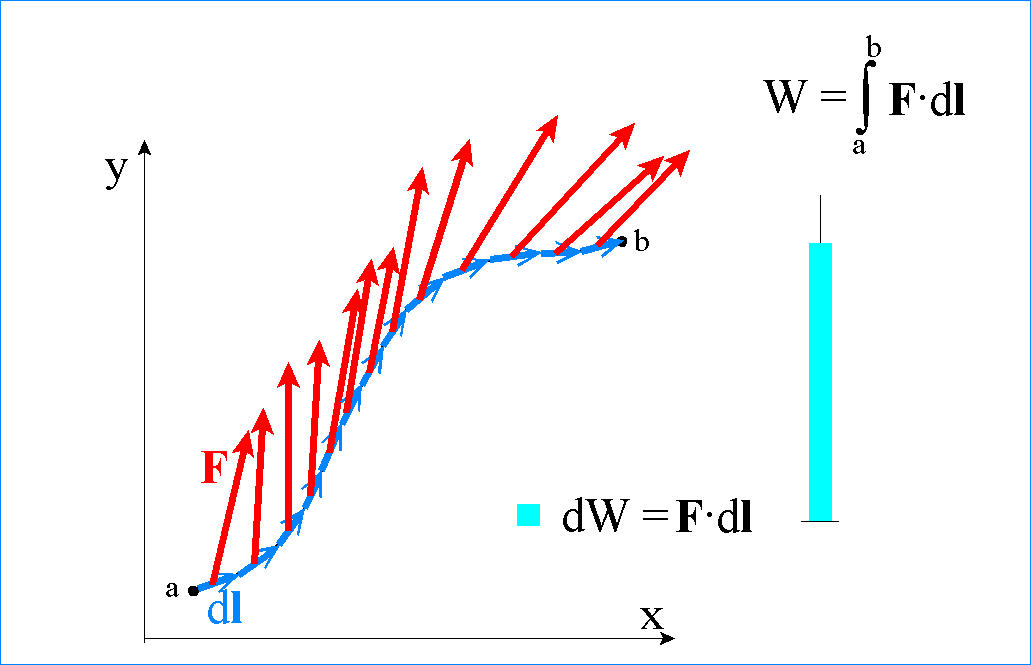
Sumując nieskończenie małe przyrosty pracy dW = F•dl korzystamy nie ze znaku sumy Σ ale, ze znaku całki ∫ , który jest przeznaczony wyłącznie po to, aby sygnalizować sumowanie wartości nieskończenie małych. Symbol całki jest stylizowaną literą S (od ‘suma’)

Dlatego sumaryczną wartość pracy zapisujemy w postaci wyrażenia

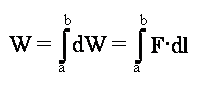
albo po prostu

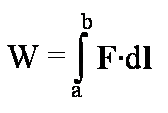
To wyrażenie na pracę sumaryczną jest także poprawne w każdym przypadku i bez żadnych ograniczeń.

Przykładem pracy wykonanej przez siłę zmienną w czasie może służyć praca wykonana w trakcie ściskania sprężyny. Po ściśnięciu sprężyny o odległość x pojawia się siła skierowana przeciwnie do kierunku ściskania

Praca wykonana przy ściskaniu sprężyny od odległości x₁ do odległości x₂ będzie wyrażona przez całkę

Stąd energia potencjalna sprężyny zdeformowanej elastycznie wynosi

Tarcie posuwiste

Tarciem nazywamy siłę, która stanowi opór dla ruchu jednej powierzchni względem innej powierzchni, kiedy obie te powierzchnie pozostają w kontakcie ze sobą. Dla ciała spoczywającego na poziomej powierzchni istnieje prostopadła do tej powierzchni siła nacisku F_n działająca między tym ciałem a powierzchnią podłoża. Jeżeli do tego ciała zostanie przyłożona pozioma siła F usiłująca przesunąć to ciało w prawo wtedy pojawi się siła tarcia F_t, skierowana w lewo i równa sile F, która powoduje, że ciało nadal pozostanie w spoczynku. Jeżeli siła F skierowana w prawo będzie wzrastała wtedy siła tarcia F_t będzie również rosła aż do momentu, kiedy ciało ruszy z miejsca. W chwili, kiedy ciało ruszy z miejsca w prawo, siła tarcia F_t osiąga swoją wartość graniczną F_s, która jest maksymalną wartością siły tarcia między ciałem i podłożem. Wartość granicznej siły tarcia F_s, nazywanej siłą tarcia statycznego, jest określona przez wyrażenie

gdzie μ_s nosi nazwę współczynnika tarcia statycznego. Wartość współczynnika μ_s zależy od rodzajów obu stykających się powierzchni, ciała i podłoża.

Kiedy ciało porusza się już ze stałą prędkością, wtedy wartość siły tarcia F_t spada do wartości F_k, nazywanej siłą tarcia kinetycznego, równej

tutaj μ_k nosi nazwę współczynnika tarcia kinetycznego. Siła tarcia kinetycznego F_k jest zawsze mniejsza od siły tarcia statycznego F_s. Przyjmujemy także, że oba współczynniki μ_s i μ_k są niezależne od wielkości pól powierzchni stykających się ze sobą a współczynnik μ_k jest niemal niezależny od prędkości, z jaką ciało przesuwa się po podłożu.

Powodem powstania sił tarcia jest fakt, że nawet bardzo gładkie powierzchnie mają w skali mikroskopowej wiele nierówności, które powodują, że rzeczywista powierzchnia styku ciała i podłoża jest o wiele mniejsza od ich powierzchni geometrycznych. Bardzo duże ciśnienia w obrębie stykających się nierówności powodują, że obie powierzchnie ulegają lokalnemu zespoleniu (zespawaniu). Kiedy rozpoczyna się ruch ciała po podłożu wtedy punkty zespoleń zostają zerwane i ruch obu powierzchni jest znacznie ułatwiony. Tym tłumaczymy fakt, że siła tarcia kinetycznego F_k jest mniejsza od siły tarcia statycznego F_s

Tarcie potoczyste

Tarciem potoczystym nazywamy tarcie między toczącym się kołem (walcem) a płaskim podłożem, po którym koło się toczy. W rezultacie niewielkich odkształceń obu stykających się powierzchni pojawia się siła tarcia ze składową F_r, która przeciwstawia się temu ruchowi. Jeżeli F_n jest siłą prostopadłą do podłoża wtedy

gdzie μ_r nosi nazwę współczynnika tarcia potoczystego.

Moc jest prędkością wykonywania pracy. Moc chwilowa, czyli dokładna wartość mocy w pewnym momencie czasu wynosi:

Jednostką mocy w układzie SI jest wat: 1 W = 1J/1s

Inną często używaną jednostką jest koń mechaniczny: 1 KM = 0.746 kW

Back to Index