DYNAMIKA RUCHU
LINIOWEGO
* Pęd
* Impuls
* Najważniejsze prawo mechaniki
W kinematycznym opisie drogi, prędkości i przyśpieszenia nie braliśmy pod uwagę przyczyn powodujących ruch ciała. Opisem ruchu odbywającego się pod działaniem siły zajmuje się dynamika, najbardziej rozbudowana część mechaniki.
Odwiecznym zagadnieniem dynamiki był opis ruchu ciał niebieskich, głównie planet. Współczesny opis tego ruchu zaangażował najtęższe umysły w przeciągu kilkuset lat. Najważniejsze etapy w historii tych odkryć można wypunktować następująco:
* Mikołaj Kopernik (1473 – 1543) i stwierdzenie, że ruch planet odbywa się wokół Słońca po torach kołowych;
* Tycho de Brahe (1546 – 1601) nie wierzył w model Kopernika ale wykonał niezwykle dokładne pomiary pozornych ruchów planet;
* Johannes Kepler (1571 – 1630) wykorzystał pomiary Tycho de Brahe i na ich podstawie ustalił trzy prawa poprawnie opisujące tory planet, a więc znalazł odpowiedź na pytanie JAK.
Prawa Keplera można sformułować następująco:
I. Wszystkie planety poruszają się po orbitach eliptycznych ze Słońcem w jednym z ognisk

II. Linia łącząca planetę ze Słońcem zakreśla jednakowe powierzchnie A w płaszczyźnie orbity w tych samych przedziałach czasu; oznacza to, że „prędkość polowa” dA/dt planety na orbicie eliptycznej jest stała.
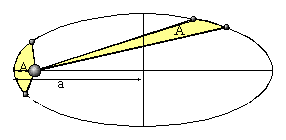
III. Stosunek kwadratów okresów obiegu planet wokół Słońca jest równy stosunkowi trzecich potęg długich osi ich orbit eliptycznych
![]()
Zasadniczymi prawami, które zrewolucjonizowały sposób opisu zachowania się ciał poddanych działaniu sił są trzy prawa ruchu Newtona. W ich sformułowaniach pojawiają się dwie nowe wielkości, niezwykle ważne w całej fizyce: siła i masa. Po wprowadzeniu masy, obiekty fizyczne przestały już być punktami matematycznymi, jak to jest w kinematyce, ale w dynamice są nazywane „ciałami”.
Isaac Newton (1642 – 1727) swoimi prawami dynamiki w połączeniu z jego prawem grawitacji wykazał, że planety rzeczywiście muszą poruszać się po orbitach eliptycznych ze Słońcem w ich ogniskach, czyli potwierdził model Keplera. Zatem Newton już wiedział JAK ale i DLACZEGO planety wykonują swoje wędrówki wokół Słońca.
Newton znakomicie zdawał sobie sprawę z doniosłości znaczenia odkrytych przez siebie praw ruchu. One właśnie, w połączeniu z odkrytym także przez Newtona prawem grawitacji, pozwoliły w zaskakująco prosty sposób opisać matematycznie tory planet. Opis ten jest ścisły w przypadku dwóch ciał niebieskich obracających się wokół wspólnego środka masy. Jednak w przypadku większej liczby ciał można uzyskać jedynie przybliżone rozwiązanie (tzw. zagadnienie wielu ciał), ale wciąż na gruncie ścisłych praw ruchu Newtona. Dodatkowa komplikacja pojawia się w razie konieczności uwzględnienia w ruchu planet efektów wynikających z ogólnej teorii względności Einsteina. Tak się dzieje w przypadku Merkurego, którego orbita z eliptycznej przechodzi w kształt rozety.

Prawa ruchu Newtona w ich podstawowym sformułowaniu mają następujące brzmienie:
|
I. prawo ruchu Newtona:
Równowaga Każde ciało
pozostaje w spoczynku albo porusza się ruchem jednostajnym prostoliniowym tak
długo, dopóki nie działa na to ciało jakakolwiek siła. |
|
Pod
działaniem siły F ciało uzyskuje przyśpieszenie a wprost proporcjonalne do
tej siły. Współczynnikiem proporcjonalności jest masa ciała m.
|
|
III. prawo ruchu Newtona:
Reakcja Każde
oddziaływanie wywołuje przeciwną mu reakcję. Oznacza to, że wzajemne
oddziaływania dwóch ciał na siebie mają zawsze taką samą wartość i są
skierowane w przeciwnych kierunkach. |

Ciało w
ruchu jest charakteryzowane przez wielkość zwaną pędem,
który może zostać zmieniony jedynie pod działaniem siły przyłożonej do tego
ciała. Pędem p nazywamy iloczyn masy ciała m i jego prędkości v
![]()


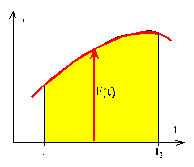
Wpływ, jaki wywiera siła F przyłożona do ciała zależy nie
tylko wartości tej siły, ale także i od długości przedziału czasu w jakim ta
siła działa. Wpływ ten charakteryzuje wielkość zwana impulsem, opisywana przez
całkę:
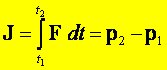
Jest to relacja całkowa wiążąca wektor impulsu (całkę po czasie z działającej siły) ze zmianami wektora pędu w dwóch różnych momentach czasu odpowiadających granicom całkowania. Wektor impulsu J jest równy zmianie pędu ciała pod wpływem siły F (stałej lub zmiennej) działającej w dłuższym przedziale czasowym między czasem t1 a czasem t2

Równanie ![]() jest niezwykle
użyteczne w większości zagadnień dynamiki, ale ma jedno zasadnicze
ograniczenie: jest ono słuszne tylko w przypadku, kiedy masa ciała m jest
stała. Nie stosuje się zatem do opisu np. ruchu rakiet i samolotów odrzutowych,
których masa zmniejsza się istotnie w czasie ich ruchu. Nie jest także słuszne
w przypadku cząstek poruszających się z dużymi szybkościami v, których masa m
rośnie relatywistycznie wraz z ich prędkością v wg równania
jest niezwykle
użyteczne w większości zagadnień dynamiki, ale ma jedno zasadnicze
ograniczenie: jest ono słuszne tylko w przypadku, kiedy masa ciała m jest
stała. Nie stosuje się zatem do opisu np. ruchu rakiet i samolotów odrzutowych,
których masa zmniejsza się istotnie w czasie ich ruchu. Nie jest także słuszne
w przypadku cząstek poruszających się z dużymi szybkościami v, których masa m
rośnie relatywistycznie wraz z ich prędkością v wg równania
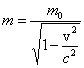
gdzie m0 jest masą spoczynkową cząstki, a c jest prędkością światła w próżni.
Prawdziwym królem dynamiki jest równanie, które nie ma tego ograniczenia i jest słuszne w każdym przypadku. Jest to równanie, które możemy nazwać uogólnioną II. zasadą dynamiki Newtona i w którym siła działająca na ciało jest wyrażona jako prędkość zmiany pędu tego ciała:
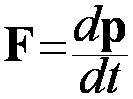
Druga zasada dynamiki Newtona sformułowana w równaniu 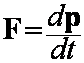 jest relacją różniczkową wiążącą wektor siły z prędkością zmian
wektora pędu w każdym momencie czasu.
jest relacją różniczkową wiążącą wektor siły z prędkością zmian
wektora pędu w każdym momencie czasu.
Jeżeli masa ciała jest stała w czasie ruchu, to równanie 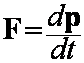 przechodzi
natychmiast w znane nam proste równanie
przechodzi
natychmiast w znane nam proste równanie ![]() .
.

Z uogólnionej II zasady dynamiki Newtona wynika bardzo ważne
i użyteczne prawo zachowania pędu, które stosuje się do układów izolowanych,
czyli mających stałą masę i na które nie działają żadne siły zewnętrzne. Prawo
to orzeka, że całkowity pęd układu izolowanego jest
stały w czasie. Rzeczywiście, ponieważ 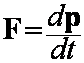 , to gdy nie działają siły zewnętrzne, czyli F = 0,
wtedy
, to gdy nie działają siły zewnętrzne, czyli F = 0,
wtedy
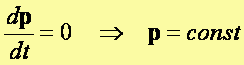
Ostatnia relacja jest tożsama z I. zasadą dynamiki Newtona: stan ruchu może zostać zmieniony tylko pod działaniem sił zewnętrznych.
