Back to Index

KINEMATYKA RUCHU LINIOWEGO

* Droga, prędkość i przyśpieszenie w ruchu liniowym

* Ruch jednostajny po okręgu – przyśpieszenie dośrodkowe

* Energia kinetyczna ruchu liniowego

* Szczególna teoria względności

* Eksperyment Michelsona i Morley’a

* Postulaty szczególnej teorii względności

* Jednoczesność i skrócenie przedziału czasowego

* Paradoks bliźniąt

* Transformacje Galileusza i transformacje Lorentza

* Relatywistyczne dodawanie prędkości

* Skrócenie odcinka w ruchu

* Relatywistyczna masa i relatywistyczny pęd. E = mc²

* Związek między pędem i energią

Kinematyka jest tą częścią mechaniki, która opisuje matematycznie sam ruch ciała bez uwzględniania jakichkolwiek czynników powodujących ten ruch lub jego zmiany.

Podstawowymi wielkościami w kinematyce są trzy wielkości wektorowe: droga s, prędkość v i przyśpieszenie a oraz czas t będący wielkością skalarną.

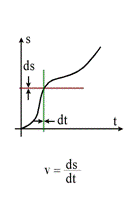
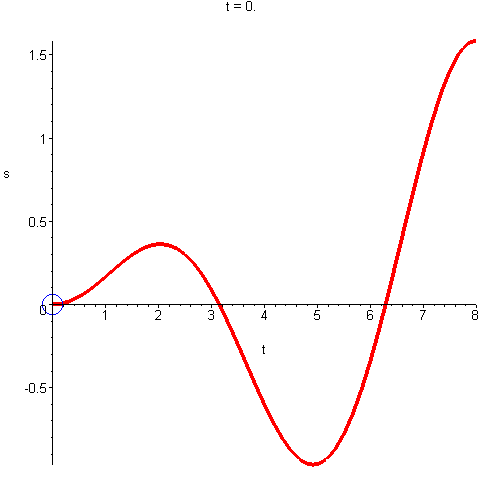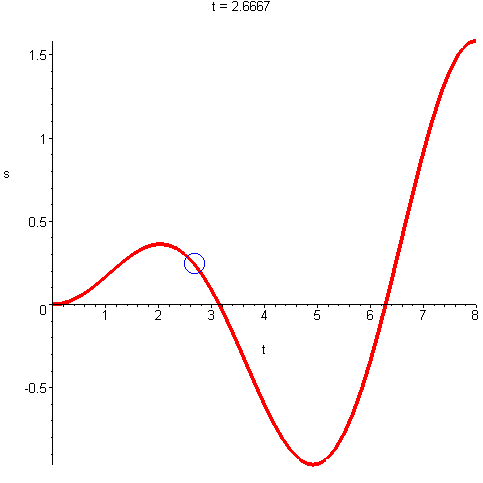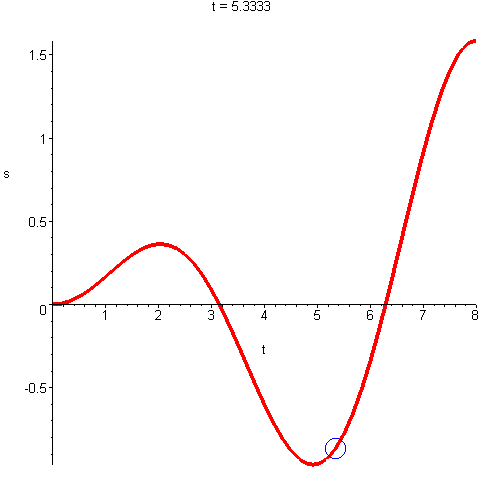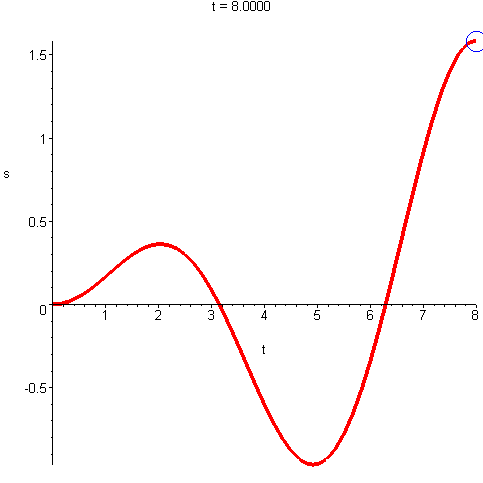
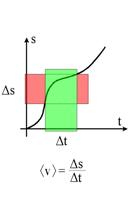
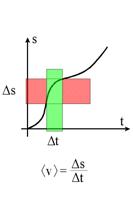
Określając prędkość liniową ciała na podstawie wykresu drogi tego ciała jako funkcji czasu otrzymujemy tym dokładniejszy wynik na prędkość chwilową im mniejszy przedział czasowy bierzemy pod uwagę. Przy dużych przedziałach czasowych Δt mamy duże odcinki drogi Δs i w rezultacie otrzymujemy prędkość średnią w tych przedziałach

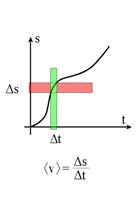
Aby otrzymać dokładną prędkość chwilową w pewnym momencie musimy zawęzić przedział czasowy do nieskończenie krótkiej, ale niezerowej, chwili, którą oznaczamy przez dt. Wtedy przebyta droga także będzie nieskończenie krótka, oznaczana przez ds, a otrzymanym przez nas wynikiem będzie dokładna wartość prędkości chwilowej v:

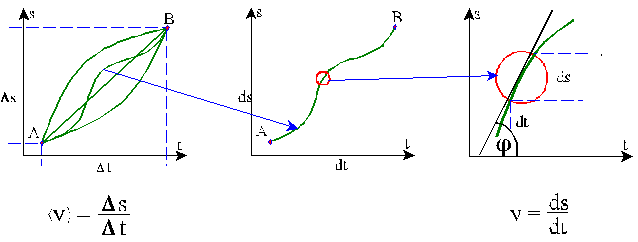
Nieskończenie małe, ale niezerowe, przyrosty wielkości oznaczamy symbolem d (od łac. differentia) i nazywamy różniczkami. Np. różniczkami drogi s, współrzędnej x, czasu t lub jakiejkolwiek wielkości A będą odpowiednio ds, dx, dt i dA.

Stosunek różniczek dwóch wielkości nazywamy pochodną pierwszej z nich względem drugiej. Np. pochodna drogi względem czasu ds/dt jest znaną nam już prędkością v.

Zawsze pochodna względem czasu jest prędkością zmian dowolnej wielkości A w czasie.

Jeżeli jest niezerowa, to A zmienia się na pewno, rośnie gdy ta pochodna jest dodatnia i maleje, gdy ta pochodna jest ujemna.

Przyrost drogi liniowej ds jaką przebywa punkt o współrzędnych (x, y, z) jest równy sumie przyrostów tych współrzędnych dx, dy i dz pomnożonych przez wersory osi układu odniesienia

Prędkość liniowa v jest prędkością zmian drogi liniowej

Przyśpieszenie liniowe a jest prędkością zmian prędkości liniowej

W kinematyce, ruch ciała nie musi odbywać się tylko do przodu. Możliwe jest także cofanie się. Wtedy przyrost drogi ds jest ujemny. Ujemne mogą być też prędkość v i przyśpieszenie a.

Wartość prędkości, czyli długość wektora prędkości, nazywamy szybkością. Jeżeli ciało porusza się po okręgu o stałym promieniu R ze stałą szybkością (ruch jednostajny), np. 10 m/s, to nie znaczy, że ma ono stałą prędkość. Wektor prędkości liniowej jest tutaj stale styczny do toru ruchu i jeżeli ciało zmienia położenie to ten wektor też ulega zmianie – zmienia się jego kierunek, czyli zmienia się cały wektor. Jeżeli jednak wektor prędkości ulega zmianie, to musi wystąpić przyśpieszenie.

Przyśpieszenie występujące w ruchu jednostajnym po okręgu nazywamy przyspieszeniem dośrodkowym. Wartość przyśpieszenia dośrodkowego znajdziemy na podstawie konstrukcji przedstawionej na rysunku

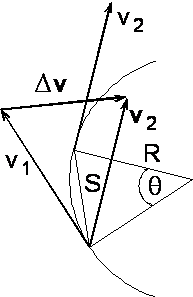
Bierzemy wektory prędkości v₁ i v₂ w dwóch bliskich punktach toru i sprowadzamy wektor v₂ do wspólnego początku z wektorem v₁. Aby otrzymać późniejszy wektor v₂ musimy do wcześniejszego wektora v₁ dodać pewien wektor Δv.

Na podstawie podobieństwa trójkątów znajdujemy, że

stąd przyspieszenie

czyli

Na wartość przyśpieszenia dośrodkowego otrzymaliśmy zatem wyrażenie

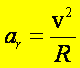
Im krótszy weźmiemy odcinek S, tym bardziej kierunek wektora Δv będzie się zbliżał do kierunku promienia R (kąt między wektorami v i Δv będzie zbliżał się do 90^o). Stąd termin ‘przyśpieszenie dośrodkowe’.

Tutaj pojawia się znakomita okazja, aby wyjść poza kinematykę i nawiązać do dynamiki ruchu. Jeżeli ciało ma pewną masę i jest w czasie ruchu po okręgu trzymane na lince, to siła z jaką musimy ciągnąć linkę nosi nazwę siły dośrodkowej, natomiast siła z jaką ciało usiłuje wyrwać linkę z rąk nosi nazwę siły odśrodkowej. Jeżeli ruch jest stacjonarny, czyli stałe są szybkość ciała oraz promień toru, to obie te siły muszą mieć jednakową wartość i być przeciwnie skierowane.

Jeżeli ciało o masie m porusza się z prędkością v to ma ono energię kinetyczną ruchu liniowego

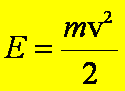
Tutaj można wspomnieć, że oprócz energii kinetycznej (energii ruchu) ciało może mieć energię potencjalną wynikającą z jego położenia w jakimś polu sił (grawitacyjnym, elektrycznym) lub z jego szeroko pojętej konfiguracji (kamień leżący na zboczu góry, naciągnięta guma, ładunek wybuchowy umieszczony w granacie itp.).

Szczególna teoria względności została stworzona przez A. Einsteina w r. 1905. Teoria ta opisuje odchylenia, niekiedy bardzo znaczne, takich wielkości kinematycznych jak prędkość upływu czasu, wartość przedziału czasowego czy długość odcinka, jakie obserwuje się wtedy, kiedy w grę wchodzą prędkości porównywalne z prędkością światła. Teoria ta zakłada, że wszystkie prawa fizyczne są identyczne we wszystkich układach odniesienia i że prędkość światła w próżni c jest stała w całym Wszechświecie i jest niezależna od prędkości obserwatora. Konsekwentne stosowanie tych założeń prowadzi do niezwykle ważnych stwierdzeń, że masa ciała rośnie wraz z jej prędkością oraz że masa i energia są sobie równoważne, co stanowi treść najsławniejszego wzoru fizyki E = mc².

Jedną z dawniej przyjmowanych teorii rozchodzenia się światła był model oparty na założeniu, że Wszechświat jest zanurzony w nieważkim, ale sprężystym ośrodku zwanym eterem. Strumień światła miał być falą rozchodzącą się w tym eterze. W celu wykrycia ruchu Ziemi względem eteru A. Michelson zaproponował eksperyment interferometryczny, który po istotnych udoskonaleniach wykonał wraz z E. Morley’em. Gdyby w tym eksperymencie wykryto ruch Ziemi względem eteru to założenie Einsteina o niezależności prędkości światła od prędkości obserwatora nie mogłoby zostać utrzymane.

Eksperyment został zaprojektowany w celu pomiaru prędkości hipotetycznego eteru. Ten sławny eksperyment jest oparty na zasadzie przedstawionej na rysunku.

Interferometr M-M pływał w basenie z rtęcią, aby stworzyć warunki do gładkiego obrotu o 90^o. Wektor prędkości Ziemi jest skierowany wzdłuż jednego z ramion interferometru. O tym, czy w centrum obrazu interferencyjnego pojawi się interferencja destruktywna, czy konstruktywna decyduje względna faza obu wiązek po ich przejściu przez oddzielne drogi. Gdy wektor prędkości Ziemi v jest skierowany wzdłuż ramienia l₂, to całkowity czas przejścia wiązki 2 jest

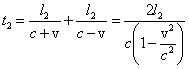
Wiązka 1 porusza się ukośnie względem wiatru eteru z prędkością

Zatem czas t₁ wynosi

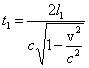
Jeżeli l₁ = l₂ = l, wtedy wiązka 1 będzie opóźniona względem wiązki 2 o wartość

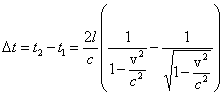
Ponieważ nie jest możliwe niezależne ustawienie warunku l₁ = l₂, to Michelson i Morley zauważyli, że mogą zarejestrować różnicę faz (przyjmując, że v = 0), gdy obrócą interferometr o 90^o, co powinno spowodować przesunięcie obrazu interferencyjnego. Następnie role wiązek 1 i 2 zostaną zamienione i w obróconej pozycji interferometru czasy (oznaczone przez primy) będą

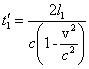oraz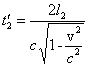

Przesunięcie czasowe między obiema wiązkami w pozycji przed obróceniem interferometru (nie primowane) będzie

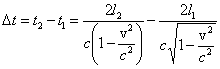
W pozycji po obrocie, przesunięcie czasowe między wiązkami wyniesie

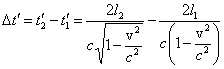
Po wykonaniu rotacji interferometru przesunięcie obrazu interferencyjnego będzie określone przez różnicę

Przy założeniu, że v n c, możemy zastosować rozwinięcie dwumienne

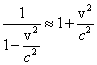oraz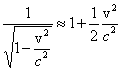

i otrzymujemy

Przyjmując za prędkość Ziemi v = 3.0 × 10⁴ m·s^-1 oraz dla l₁ i l₂ ok. 11 m (w eksperymencie Michelsona i Morley’a), otrzymuje się przesunięcie ok. 0.4 prążka. Michelson i Morley byli w stanie łatwo zarejestrować to przesunięcie, ponieważ ich aparatura miała zdolność wykrywania przesunięcia o wartości ok. 0.01 prążka. Nie zauważyli jednak żadnego znaczącego przesunięcia.

Pierwszy postulat (zasada względności):

Prawa fizyki mają tę samą postać we wszystkich inercjalnych układach odniesienia.

Drugi postulat (stałość prędkości światła):

Światło porusza się w próżni ze stałą prędkością c niezależną od prędkości źródła i obserwatora.

Dwa zdarzenia, które są jednoczesne dla jednego obserwatora, nie muszą być koniecznie jednoczesne dla drugiego obserwatora. Czy czas może biegnąć różnie w dwóch układach odniesienia? To jest właśnie to, co przewiduje teoria względności Einsteina. Punkt widzenia jednego obserwatora, znajdującego się wewnątrz poruszającego się wózka jest pokazany na górnym rysunku, zaś na dolnym rysunku - punkt widzenia obserwatora stojącego na ziemi. Dla pierwszego z nich światło przebywa między źródłem a detektorem odległość 2D z prędkością c, tak, że czas potrzebny na to wynosi

Przedział czasowy Δt, mierzony przez drugiego obserwatora, może być wyliczony następująco: Światło przechodzi całkowity dystans 2√(D² + L²) i dlatego

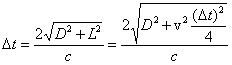
Stąd

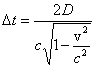
Z wyrażeń na Δt₀ i Δt eliminujemy D i znajdujemy

Znaczy to, że przedział czasowy między dwoma wydarzeniami jest dłuższy dla obserwatora spoczywającego na ziemi w stosunku do czasu, jaki rejestruje obserwator poruszający się. Jest to zasadniczym rezultatem teorii względności, zwanym dylatacją czasu: poruszające się zegary chodzą wolniej.

Δt₀ reprezentuje przedział czasowy między dwoma wydarzeniami w tym samym punkcie przestrzeni. Jest zatem nazywany czasem własnym.

Aby dolecieć do gwiazdy oddalonej od nas o 100 lat świetlnych wtedy, kiedy lecimy z prędkością v = 0.999c, potrzebujemy czasu jedynie Δt₀ = Δt √ (1-v²/c²) = 100 √ (1 - (0.999)²) = 4.5 roku.

Paradoks bliźniąt jest jednym z paradoksów szczególnej teorii względności, jakie pojawiają się z niezrozumienia zagadnienia czasu własnego. Niech w pewnym układzie inercjalnym jeden z bliźniaków porusza się od punktu A do B po torze P₁, zaś drugi z nich po torze P₂.

Prędkości obu z nich niech będą funkcjami czasu v₁(t) i v₂(t). Wtedy wiek pierwszego zwiększy się o

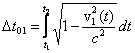
zaś drugiego o

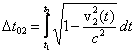
Z reguły v₁(t) i v₂(t) są różne i wiek obu bliźniaków w czasie ich spotkania będzie różny. Np., bliźniak spoczywający w przestrzeni (jego współrzędne przestrzenne nie będą się zmieniały) będzie starszy od bliźniaka podróżującego. Spowolnienie procesów w układzie poruszającym się jest sprawdzony eksperymentalnie: czas życia szybkich mezonów μ jest dłuższy niż ten czas dla mezonów powolnych.

Paradoks bliźniąt (potwierdzony ściśle także przez ogólną teorię względności) jest możliwy tylko wtedy, gdy przynajmniej jeden z bliźniaków porusza się w układzie nieinercjalnym. Wtedy procesy u obu z nich nie biegną jednakowo (nie jest spełniony pierwszy postulat teorii względności), czyli gdy pierwszy starzeje się w stosunku do drugiego, to nie znaczy, że drugi starzeje się w stosunku do pierwszego. Gdyby oba układy, w których znajdują się bliźniaki, były inercyjne, to po ich rozejściu się nie byłoby już możliwe ponowne spotkanie.

Jak transformują się położenia i prędkości z układu odniesienia poruszającego się z prędkością v w kierunku równoległym do osi x do układu spoczywającego?

Równania transformacji Galileusza: (Wielkość z indeksem 0 oznacza pomiar w układzie poruszającym się).

Dla położeń

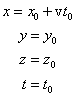
zaś dla prędkości

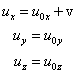
Ponieważ prędkość światła c jest niezmiennikiem, to dla prędkości relatywistycznych potrzebujemy nowych równań transformacyjnych.

Przyjmujemy, że transformacja jest liniowa i ma postać: (Wielkość z indeksem 0 oznacza pomiar w układzie poruszającym się).

Transformacja odwrotna musi mieć tę samą postać z zamianą v na -v. Zatem

Teraz jeżeli impuls światła opuszcza wspólny początek układów odniesienia s i s₀ w chwili t = t₀ = 0, to po czasie t impuls przejdzie wzdłuż osi x odległość x = ct albo x₀ = ct₀ . Zatem, z powyższych równań na x i x₀ mamy

Podstawiamy t₀ z drugiego równania do pierwszego i znajdujemy

Redukujemy t i na wartość ( otrzymujemy

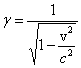
Pozostaje nam znaleźć relację między t i t₀ . Aby to zrobić, przeprowadzamy kombinację transformacji x₀ = γ(x - vt) z x = γ(x₀ + vt₀). Rozwiązujemy je względem t i znajdujemy

Podsumowując

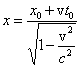
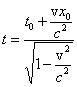
Są to tzw. transformacje Lorentza. Zostały one zaproponowane po raz pierwszy, w nieco innej postaci, przez Lorentza w r. 1904 aby wyjaśnić negatywny rezultat eksperymentu Michelsona i Morley’a i aby sprowadzić równania Maxwella do jednakowej postaci we wszystkich układach inercyjnych. Rok później Einstein otrzymał je niezależnie w oparciu o swoją teorię względności.

Z ostatniego równania widzimy, jak mieszają się ze sobą współrzędne przestrzenne i czasowe.

Poprawne relatywistycznie równania prędkości można otrzymać od razu przez różniczkowanie

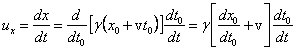
ale

oraz

zatem

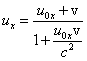
Inne składowe otrzymujemy w ten sam sposób. Ostatecznie

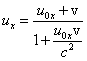
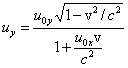
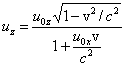
Jeżeli w układzie nieruchomym mierzymy prędkość wypadkową ciała wyrzuconego z prędkością v₂ z układu (pojazdu) poruszającego się z prędkością v₁, to w wyniku otrzymamy prędkość v równą

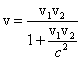
Kiedy obie prędkości są równe prędkości światła, v₁ = v₂ = c, to również v = c!

Długość odcinka mierzona w poruszającym się układzie wynosi L₀ = x₀₂ - x₀₁, zaś w układzie spoczywającym zostanie zmierzona długość L = x₂ - x₁ . Ponieważ, zgodnie z transformacjami Lorentza

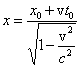
to

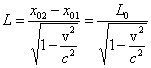
Oznacza to, że odcinek L₀ jest krótszy od L:

Podobny sens ma obecność w mianowniku transformacji Lorentza. Prosta odległość, wynikająca z transformacji Galileusza, x₀ + vt₀ powinna być zwiększona o czynnik 1/dlatego, że skróceniu ulega jednostka długości.

Einstein pokazał, że masa ciała wzrasta, kiedy wzrasta jego prędkość.

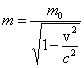
gdzie m₀ jest masą spoczynkową ciała.

Teraz pęd relatywistyczny jest wyrażony wzorem

Kiedy zastosujemy związek między siłą i prędkością zmiany pędu

to otrzymamy bardzo ważny związek między masą i energią

Kiedy do ciała zostanie przyłożona siła wypadkowa, to praca (między punktami początkowym (i) i końcowym (f)) wykonana na nadanie ciału prędkości od zerowej do v wyniesie

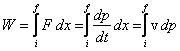
ale

zatem

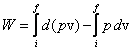
Pierwszy wyraz po prawej stronie staje się równy

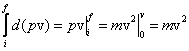
gdzie m jest funkcją prędkości v. Zatem

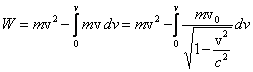
Drugi wyraz może być łatwo scałkowany, ponieważ

zatem

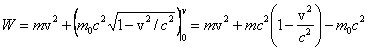
Mamy ostatecznie

Zatem relatywistyczna energia kinetyczna ciała wynosi

Całkowita energia jest równa sumie energii kinetycznej i energii spoczynkowej

Otrzymaliśmy więc sławny wzór Einsteina

Równanie na energię kinetyczną może być zapisane poprzez prędkość v

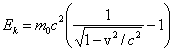
Dla małych prędkości możemy rozwinąć wyrażenie pod pierwiastkiem w szereg stosując rozkład dwumienny

Otrzymujemy zatem

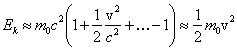
czyli zwykły wzór na energię kinetyczną.

Możemy wyprowadzić użyteczną relację między całkowitą energią E cząstki oraz jej pędem p. Ponieważ E = mc² oraz p = mv, znajdujemy

czyli

Dla cząstki w spoczynku (p = 0)

Kiedy cząstka nie ma masy spoczynkowej (foton) (m₀ = 0)

Kiedy zastosujemy na energię fotonu wzór de Broglie’a E = hν, wyrażony przez stałą Plancka h, wtedy z przyrównania pc = hν otrzymujemy

gdzie ħ = h/2π, zaś k = 2π/λ jest wektorem falowym. Pęd fotonu jest zatem równy

Analogiczny wzór opisuje pęd każdej innej cząstki, np. elektronu, protonu itd., przy czym ten wzór określa jednocześnie długość fali związanej z tą cząstką.

************

Na podstawie równoważności masy i energii dowiadujemy się, że ściśnięta lub rozciągnięta sprężyna ma większą masę niż sprężyna znajdująca się w stanie nie naprężonym. Podobnie, gorący czajnik z wodą ma masę większą od czajnika zimnego.

************

Back to Index