Back to Index

ILOCZYNY WEKTORÓW

* Mnożenie wektora przez skalar

* Iloczyn skalarny dwóch wektorów

* Iloczyn wektorowy dwóch wektorów

* Iloczyn mieszany trzech wektorów

Najprostszym mnożeniem wykonywanym na wektorach jest mnożenie wektora przez skalar (liczbę). Takie mnożenie nie zmienia kierunku wektora, ale na ogół zmienia jego długość i może zmienić jego zwrot (gdy skalar jest liczbą ujemną). Kiedy wektor A mnożymy przez skalar α to otrzymujemy nowy wektor B:

W fizyce i technice największe znaczenie mają iloczyn skalarny oraz iloczyn wektorowy dwóch wektorów. Występuje także iloczyn mieszany trzech wektorów.

Formalnie iloczyn skalarny oznaczamy kropką a jego wartość określamy przez zależność

gdzie

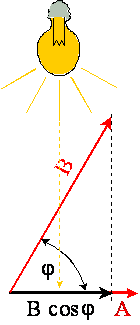
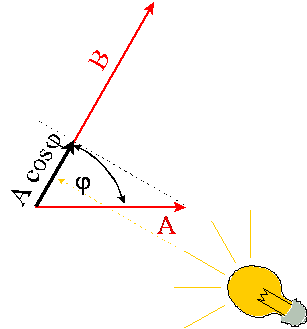
Iloczyn skalarny opisuje sposób w jaki oba wektory widzą siebie nawzajem, czyli jak długi cień rzuca każdy z wektorów na swojego partnera gdy kąt miedzy nimi wynosi φ

B cos φ jest długością cienia, jaki rzuca wektor B na wektor A. Analogicznie, A cos φ jest długością cienia, jaki rzuca wektor A na wektor B.

Widać więc, że

Oznacza to, że iloczyn skalarny jest przemienny.

Iloczyn skalarny dwóch wektorów opisuje ILOCZYN WKŁADÓW, JAKIE OBA WEKTORY WNOSZĄ DO JEDNEGO KIERUNKU.

Kiedy długość rzutu (cienia) jednego z wektorów jest zerowa, wtedy i długość rzutu drugiego wektora jest zerowa, czyli A•B = 0. Oznacza to, że te wektory w ogóle nie działają w tym samym kierunku.

Praca W, jaką wykonamy przesuwając pojazd, zależy nie tylko od przyłożonej siły F ale także od kąta, jaki tworzy kierunek działania siły z kierunkiem toru

Istotny dla wartości pracy W będzie rzut wektora F na kierunek drogi s.

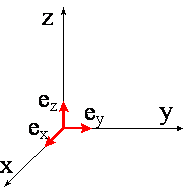
Ponieważ wektory jednostkowe osi układu odniesienia x, y i z, które oznaczamy jako wektory e_x, e_y i e_z, są do siebie wzajemnie prostopadłe, to pamiętając o tym, że A•B = AB cos φ oraz, że cos 0 = 1 i cos 90^o = 0, otrzymujemy wartości iloczynów tych wektorów jednostkowych:

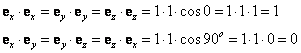
Wykonując analogiczne mnożenie na wektorach A i B

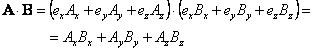
otrzymaliśmy nowe wyrażenie na wartość iloczynu skalarnego dwóch wektorów A i B

Pamiętaj, zatem

Wartość iloczynu skalarnego dwóch wektorów A i B można zapisać w postaci dwóch równoważnych wyrażeń:

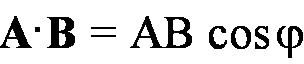
Przez porównanie obu tych wyrażeń znajdujemy wyrażenie na wartość kąta między wektorami A i B:

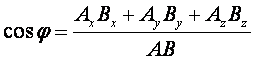
Wiele ważnych wielkości wektorowych w nauce i technice jest określone przez wektor będący produktem iloczynu dwóch innych wektorów. W takich przypadkach iloczyn tych wektorów, zwany iloczynem wektorowym, daje w wyniku trzeci wektor.

W takim przypadku zadaniem jest określenie wszystkich trzech cech wektora C będącego produktem iloczynu wektorowego wektorów A i B:

- długości

- kierunku i

- zwrotu

oraz wyrażenie ich przez składowe tych wektorów.

Iloczyn wektorowy wektorów A i B, dający w wyniku trzeci wektor C, oznaczamy ukośnym krzyżykiem

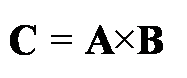
KIERUNEK

wektora C jest taki, że ten wektor jest prostopadły do płaszczyzny utworzonej przez wektory A i B, czyli jest prostopadły tak do wektora A, jak i do wektora B.

DŁUGOŚĆ

wektora C jest równa co do wartości polu równoległoboku zbudowanego na wektorach A i B. Liczbowo C = AB sin φ.

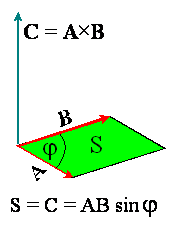
ZWROT

wektora C określa kierunek ruchu śruby prawoskrętnej w trakcie nakładania pierwszego z wektorów iloczynu, czyli A, na drugi, czyli B.

Zmiana kolejności nakładania wektorów oznacza zmianę znaku iloczynu wektorowego.

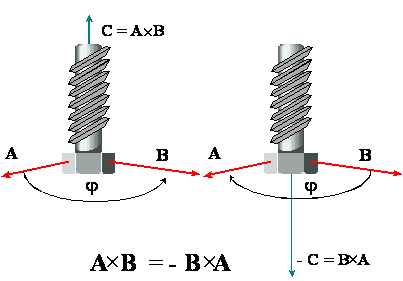
Wynika stąd ważna własność iloczynu wektorowego:

w odróżnieniu od iloczynu skalarnego, iloczyn wektorowy jest nieprzemienny (antyprzemienny).

Z iloczynem wektorowym będziemy się spotykali w czasie całego kursu fizyki. Jest on równie często spotykany w mechanice, jak i w nauce o elektryczności i magnetyzmie.

W życiu codziennym iloczyn wektorowy spotykamy w postaci momentu siły w ruchu obrotowym. Na ruch obrotowy wywieramy wpływ tym skuteczniej, im większy przyłożymy moment siły.

W czasie odkręcania nakrętki za pomocą klucza ważna jest nie tylko siła F ale także sposób jej przyłożenia (długość ramienia R i kąt jaki tworzy ramię z kierunkiem siły)

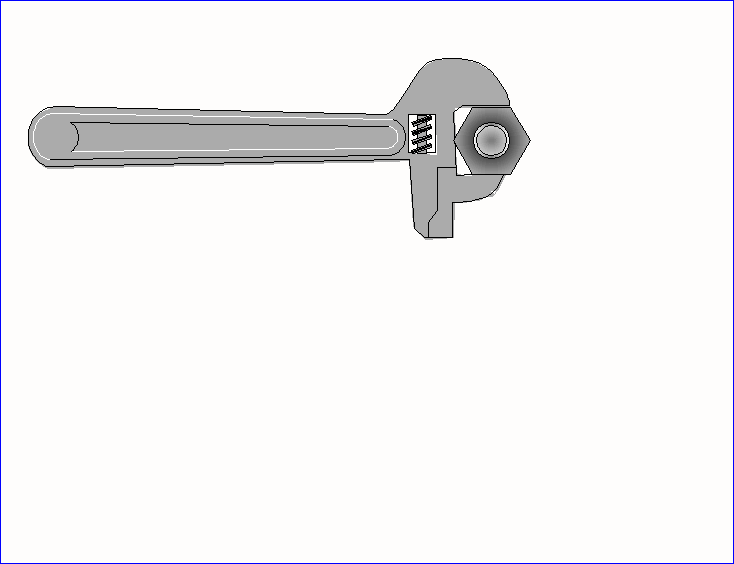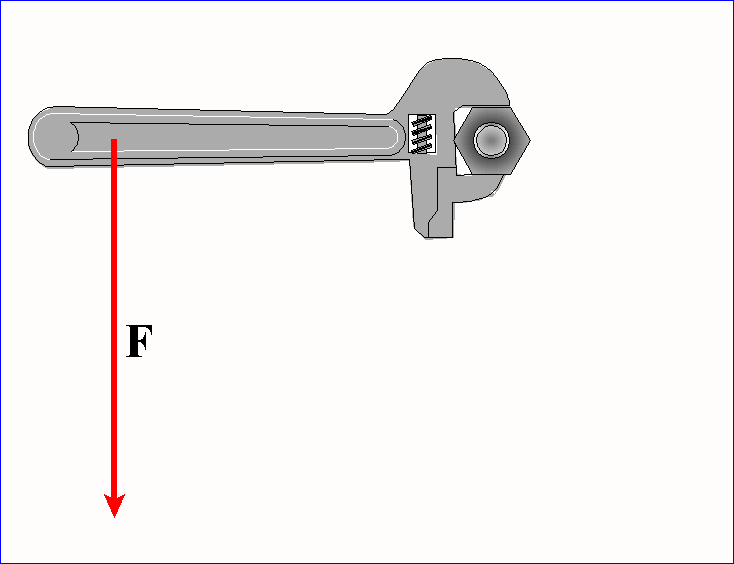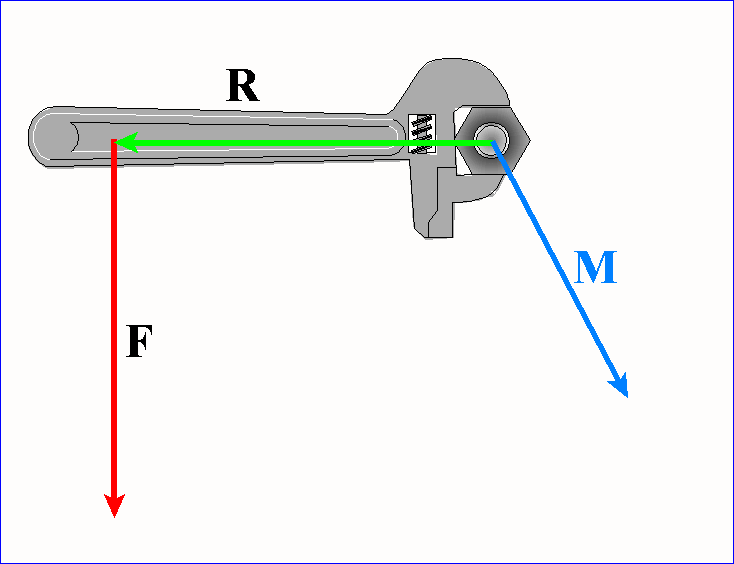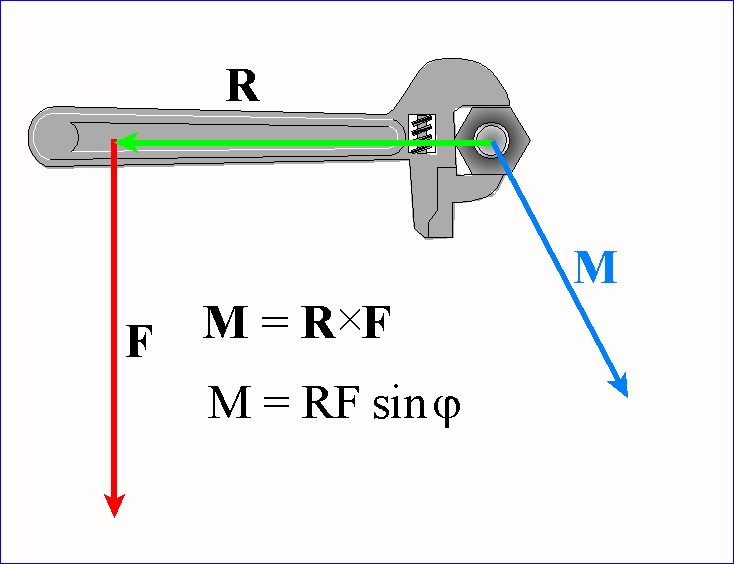
Wektor powstającego momentu siły M jest prostopadły tak do wektora R, jak i do wektora F.

Wszystkie te zależności są ujęte elegancko w jednym wyrażeniu w postaci iloczynu wektorowego:

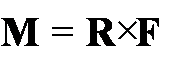
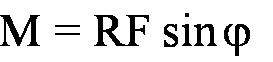
Wprawdzie składowe wektora C, będącego produktem iloczynu wektorowego wektorów A i B, są już zawarte w jego długości i kierunku, ale mając dane składowe wektorów A i B możemy za ich pomocą wyznaczyć składowe wektora C w postaci wyznacznika:

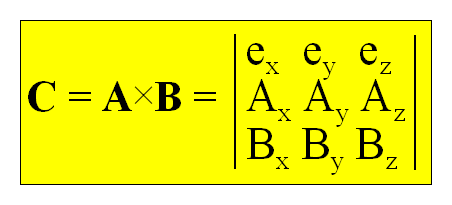
Najwygodniej obliczyć ten wyznacznik przez rozwinięcie względem pierwszego wiersza.

Iloczyn mieszany trzech wektorów jest wielkością skalarną równą wartości wyznacznika

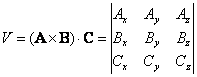
Interpretacja geometryczna: iloczyn mieszany jest liczbowo równy wartości objętości V równoległościanu rozpiętego na wektorach A, B i C:

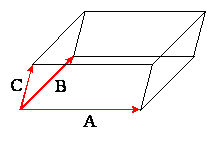
Cykliczne przestawianie wektorów w iloczynie mieszanym nie zmienia wartości tego iloczynu, czyli

Back to Index