Self-organized criticality (SOC) is a term used in physics to describe dynamical systems which have a critical point as an attractor. Their macroscopic behaviour thus displays the spatial and/or temporal scale-invariance characteristic of the critical point of a phase transition, but, unlike the latter, in SOC these features result without needing to tune control parameters to precise values. It has been argued that earthquakes, landslides, forest fires, and species extinctions are examples of self-organized criticality in nature. In addition, wars and stock market crashes have been associated with this behaviour.
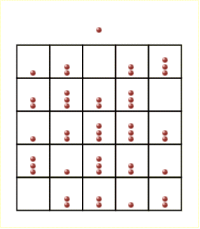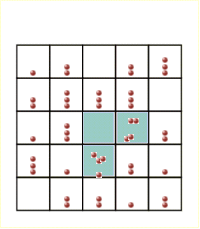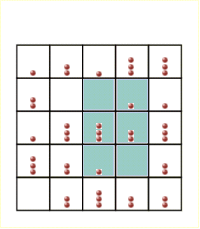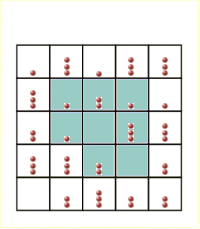
The concept of self-organized criticality was introduced to explain the behaviour of the sandpile model. In this model, particles are randomly dropped onto a square grid of boxes. When a box accumulates four particles they are redistributed to the four adjacent boxes or lost off the edge of the grid. Redistributions can lead to further instabilities with the possibility of more particles being lost from the 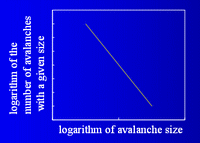 grid, contributing to the size of each avalanche. These avalanches satisfied a power-law frequency-area distribution with a slope dependend on lattice topology.
Here you can download a program (Windows version) demonstrating creation of power-law distribution in sand-pile model on a square lattice.
A number of different SOC models have been shown to generate such networks as an emergent phenomenon, as opposed to the simpler models proposed by network researchers where the network tends to be assumed to exist independently of any physical space or dynamics.
As we said previously one of the most remarkable features that characterizes self-organized criticality is the events’ power law distribution. This feature, combined with the abundance of real-world networks with scale-free degree distribution, may give rise to the suspicion that a relationship exists between the two issues.
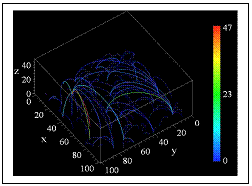 A real link between the two phenomena has been established for the first time by Hughes et al. in a rather complex model for cascades of magnetic field lines’ reconnection in the solar atmosphere using a plausible number of processes associated to diffusion of sun spots and reconnection of crossing field lines. In the model multiple directed magnetic loops evolve in space and time. Loops injected at small scales are anchored by footpoints of opposite polarity moving randomly on a surface. Nearby footpoints of the same polarity aggregate, and loops can reconnect when they collide. This may trigger a cascade of further reconnection, representing a solar flare. Numerical simulations showed that a power law distribution of flare energies emerges, associated with a scale-free network of loops, indicating self-organized criticality.
A much simpler model, assuming only two processes, merging and creation, in an on going dynamics of vertices connected in a network has been proposed by Sneppen et al. The model provides a generic framework to generate networks with large-scale features from small-scale excitations under steady state conditions, and may thus complement preferential growth which provides scaling only under persistently growing conditions
Another path of investigation has been proposed by Goh et al. The authors used the complex network as a base structure where the snadpile 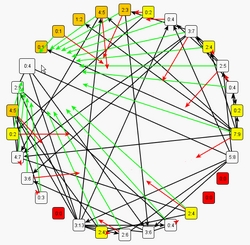 dynamics occurs. They study relations between the exponent of a network’s degree distribution and the exponent of an avalanche’s size distribution. Fronczak et al. extended Goh’s idea to the model where the networks’ degree distribution changes due to the sandpile’s avalanches’ distribution on this network and the avalanches’ size distribution changes because the network structure evolves. These two mechanisms influence each other and lead to the equilibrium point at which the avalanches’ distribution’s and the degree distribution’s shapes become very similar.
Click on image to see the animation (AVI, 4.4MB).
Here you can find explanations.
- Solar Flares as Cascades of Reconnecting Magnetic Loops
D. Hughes, M. Paczuski, R. O. Dendy, P. Helander, and K. G. McClements
Phys. Rev. Lett. 90, 131101 (2003)
- A simple model for self organization of bipartite network
Kim Sneppen, Martin Rosvall, Ala Trusina, and Petter Minnhagen
Europhys. Lett., 67 (3), pp. 349-354 (2004)
- Sandpile on Scale-Free Networks
K.-I. Goh, D.-S. Lee, B. Kahng, and D. Kim
Phys. Rev. Lett. 91, 148701 (2003)
- Self-organized criticality and coevolution of network structure and dynamics
P. Fronczak, A. Fronczak, and J. A. Holyst
Phys. Rev. E 73, 046117 (2006)
|
