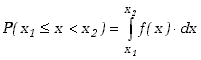 .
.
Rozkład Gaussa jest rozkładem gęstości prawdopodobieństwa f(x) dla zmiennej losowej, która może przyjmować dowolne wartości rzeczywiste. Oznacza to, że prawdopodobieństwo znalezienia wartości zmiennej losowej w przedziale pomiędzy liczbami x1 i x2 dane jest wyrażeniem
|
|
(1) |
Kiedy wartość x1 we wzorze (1.6) zdąża do minus nieskończoności otrzymujemy wartość tzw. dystrybuanty rozkładu w punkcie x2
|
|
(2) |
Znając postać rozkładu dystrybuanty możemy łatwo obliczyć prawdopodobieństwo zadane całką we wzorze (1), bowiem
|
|
(3) |
Kiedy wartość x1 zdąża do minus nieskończoności, a wartość x2 zdąża do plus nieskończoności otrzymujemy warunek unormowania rozkładu
|
|
(4) |
co oznacza, że prawdopodobieństwo zdarzenia pewnego równe jest jedności.