Back to Index

STRUMIEŃ POLA E

PRAWO GAUSSA DLA POLA E.

ZASTOSOWANIA PRAWA GAUSSA DO OBLICZANIA WARTOŚCI POLA E

* Definicja strumienia pola elektrycznego

* Prawo Gaussa dla pola elektrycznego

* Zastosowania prawa Gaussa do obliczeń pola elektrycznego

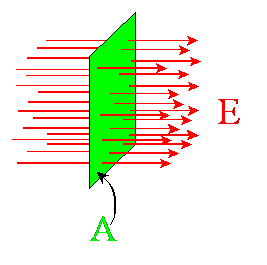
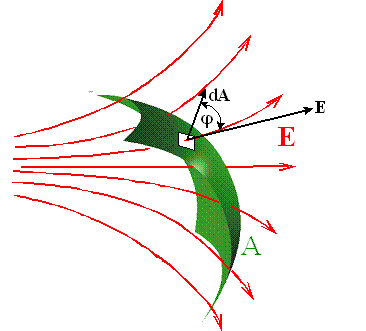
Jeżeli pole elektryczne jest jednorodne i gdy płaszczyzna o powierzchni A jest ustawiona prostopadle do linii tego pola E, to strumień pola elektrycznego Φ_E przenikający tę powierzchnię jest równy

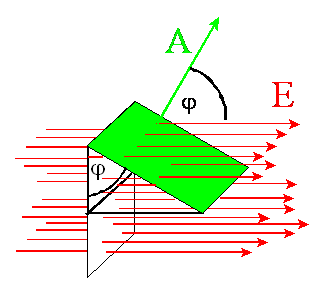
Jeżeli teraz ta powierzchnia zostanie odchylona o kąt φ od poprzedniego położenia, to strumień zmieni swoją wartość i będzie wynosił

Ponieważ strumień jest wielkością skalarną, to zależność tę dla pola jednorodnego możemy zapisać w postaci iloczynu skalarnego wektora pola E i wektora powierzchni A:

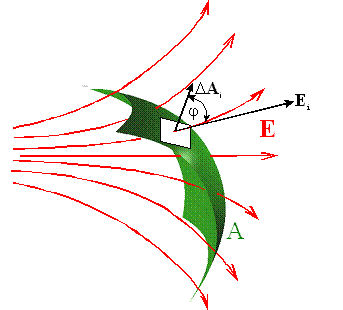
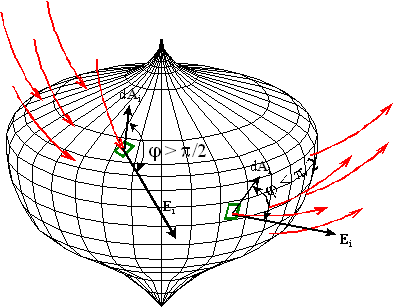
W przypadku ogólnym, gdy pole jest niejednorodne a powierzchnia nie jest płaska, wtedy przybliżone wyrażenie na strumień pola E przez płat powierzchni zakrzywionej otrzymamy przez podzielenie tego płata na pewną liczbę n małych płaskich płatów, z których każdy ma pewną małą ale skończoną powierzchnię ΔA_i. Pole elektryczne przechodzące przez powierzchnię ΔA_i ma w przybliżeniu stałą wartość E_i i przybliżoną wartość strumienia pola E otrzymamy przez zsumowanie strumieni przez poszczególne płaskie płaty

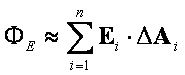
Strumieniem pola E (jednorodnego lub niejednorodnego) przechodzącego przez nieskończenie mały element powierzchni dA nazywamy iloczyn skalarny:

Strumień pola E przechodzącego przez pewien płat powierzchni A otrzymamy po zastąpieniu sumowania przez całkowanie po całym płacie A

Strumień pola E przechodzącego przez powierzchnię zamkniętą A opisujemy całką (symbol całki z kółeczkiem)

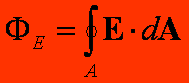
Wektor dA wybieramy tak aby był skierowany na zewnątrz powierzchni

Dla dowolnego pola wektorowego G strumień tego pola przez różne płaty powierzchniowe obrazuje animacja:

Strumień pola wektorowego można poglądowo zobrazować za pomocą linii sił tego pola.

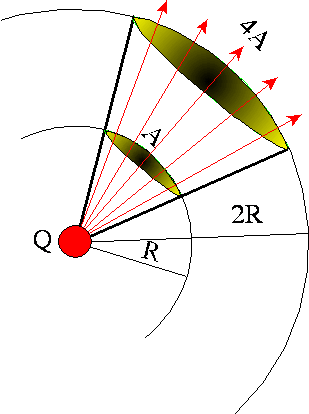
Całkowita ilość linii pola w kącie bryłowym jest taka sama w odległości 2R, jak i w odległości R. Natężenie pola jest odwrotnie proporcjonalne do R², ale pole powierzchni A jest wprost proporcjonalne do R². Tak więc iloczyn tych dwóch wielkości, 1/R²×R², jest niezależny od R.

Jeżeli wewnątrz powierzchni zamkniętej, na rysunku oznaczonej przez A₁, umieścimy ładunek dodatni +Q, to strumień pola elektrycznego przez tę powierzchnię będzie dodatni (zgodnie z naszą umową linie pola będą wychodziły z wnętrza tej powierzchni. Gdy wewnątrz innej powierzchni zamkniętej A₂ umieścimy ładunek o takiej samej wartości, ale o przeciwnym znaku, -Q, to strumień będzie ujemny (linie pola wchodzą do wnętrza) jednak wartość bezwzględna strumienia przez powierzchnię A₂ będzie taka sama, jak przez powierzchnię A₁.

Wartość strumienia nie zależy zatem od kształtu powierzchni zamkniętej, a zależy jedynie od wartości ładunku zamkniętego wewnątrz tej powierzchni. Strumień pola pochodzącego od dipola elektrycznego znajdującego się wewnątrz dowolnej powierzchni zamkniętej będzie zatem równy zeru (bo suma algebraiczna +Q i -Q wynosi zero)

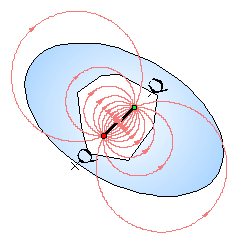
Gdyby ładunki nie były jednakowe, to strumień pola nie mógłby być zerowy. Jeżeli np. ładunek ujemny jest większy od dodatniego, to strumień pola przez powierzchnię zamkniętą jest ujemny, jak na rysunku

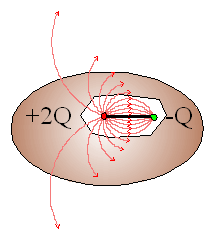
Prawo Gaussa, jedno z najważniejszych w elektrodynamice orzeka, że strumień pola elektrycznego E przez powierzchnię zamkniętą jest określony tylko przez algebraiczną sumę wszystkich ładunków elektrycznych Q zawartych wewnątrz tej powierzchni. Nie ma znaczenia jak te ładunki są rozmieszczone wewnątrz tej powierzchni.

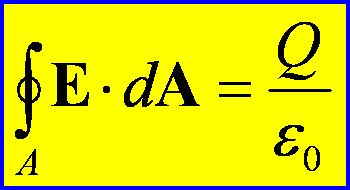
Symbol Q oznacza algebraiczną sumę ładunków znajdujących się wewnątrz powierzchni zamkniętej A, po której przeprowadzamy całkowanie (sumowanie) strumienia; g₀ jest przenikalnością elektryczną próżni.

Nie ma żadnego znaczenia, jak ładunki wewnątrz powierzchni A są rozłożone. Jednocześnie, na wartość sumarycznego strumienia pola elektrycznego nie mają żadnego wpływu ładunki, które znajdują się na zewnątrz powierzchni A, nawet te przylepione do jej strony zewnętrznej.

Prawo Gaussa dla pola elektrycznego jest uogólnionym sformułowaniem zależności między ładunkami a polami elektrycznymi i jest jednym z czterech równań Maxwella opisujących całość zjawisk elektrycznych i magnetycznych.

Mając zadany rozkład ładunku możemy za pomocą prawa Gaussa dla pola elektrycznego obliczyć wartość pola elektrycznego w określonym punkcie lub obszarze. Kluczową czynnością jest otoczenie odpowiedniego obszaru ładunku stosownie wybraną powierzchnią zamkniętą. Chociaż prawo Gaussa jest spełnione dla każdej powierzchni zamkniętej A, to jednak wybór tej powierzchni powinien być taki, aby całkowanie po niej byla najłatwiejsze. W przytoczonych przykładach sugerowana powierzchnia Gaussa jest na rysunku oznaczona czerwonym konturem.

1. Prawo Coulomba jest zawarte w prawie Gaussa, ale ono samo jest zależnością eksperymentalną, którą wykorzystywaliśmy przy wyprowadzaniu prawa Gaussa.

Prawo Gaussa jest zatem ogólniejsze od prawa Coulomba: nie można wyprowadzić prawa Gaussa z prawa Coulomba, ale prawo Coulomba otrzymuje sie z prawa Gaussa bardzo łatwo. Wystarczy znaleźć siłę F = qE, działającą na ładunek punktowy q znajdujący się w odległości r od innego ładunku punktowego Q. Aby wyznaczyć F musimy znać tylko E, a to znajdziemy z prawa Gaussa. Ładunek Q umieszczamy w środku sfery o promieniu r, jak na rysunku

Pole E pochodzące od ładunku Q ma na powierzchni sfery jednakową wartość i wszędzie na tej powierzchni wektor E jest równoległy do wektora dA. Po zastosowaniu prawa Gaussa otrzymamy

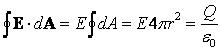
czyli

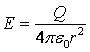
Ponieważ wektor E jest skierowany wzdłuż promienia r, to

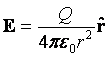
Zgodnie z definicją pola E, siła działająca na ładunek q wynosi

Otrzymaliśmy zatem prawo Coulomba z prawa Gaussa:

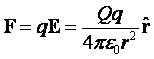
2. Pole naładowanej sfery przewodzącej o promieniu r (wewnątrz sfery nie ma ładunków):

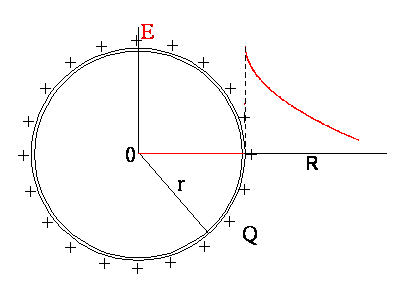
Na podstawie prawa Gaussa, pole na zewnątrz sfery w odległości R od jej centrum wynosi , czyli

Wewnątrz sfery (Q = 0) pole

3. Pole jednorodnie naładowanej kuli dielektrycznej. Całkowity ładunek zawarty w kuli jest Q.

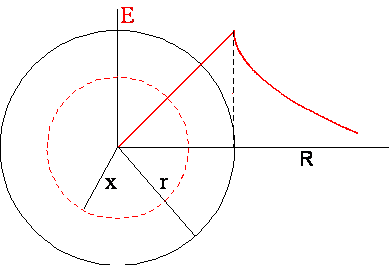
Obliczając pole E w odległości x od środka kuli oznaczamy przez q ładunek zawarty w kuli o promieniu x. Z prostej proporcji

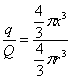otrzymujemy . Na podstawie prawa Gaussa szukane pole E wewnątrz kuli wynosi , czyli . Zatem pole wewnątrz kuli rośnie liniowo wraz ze wzrostem x. Na zewnątrz kuli pole maleje ze wzrostem odległości od środka (patrz poprzedni przykład).

4. Pole ładunku liniowego oraz naładowanego cylindra przewodzącego o gęstości liniowej ładunku 8[C/m]:

Na odcinku L przewodnika znajduje się ładunek Q = 8L, zatem z prawa Gaussa otrzymujemy . Stąd znajdujemy szukane pole

5. Pole naładowanej nieskończonej płaskiej warstwy

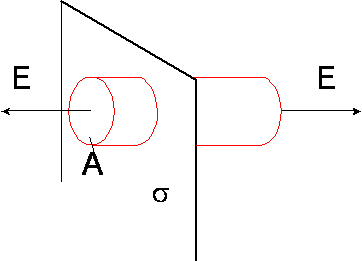
Pole jest jednorodne i rozciąga się w obie strony prostopadle do powierzchni płyty (przechodzi tylko przez podstawy walca). Z prawa Gaussa otrzymujemy

6. Pole naładowanej nieskończonej płaskiej płyty przewodzącej

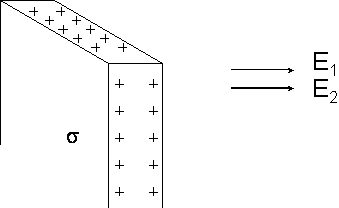
Ładunek na płycie przewodzącej jest rozmieszczony na obu jej powierzchniach. Ponieważ mamy dwie warstwy ładunkowe o gęstości ładunku σ każda, to na podstawie wyniku poprzedniego przykładu natężenie pola będzie dwukrotnie wyższe.

7. Pole między przeciwnie naładowanymi równoległymi płytami przewodzącymi

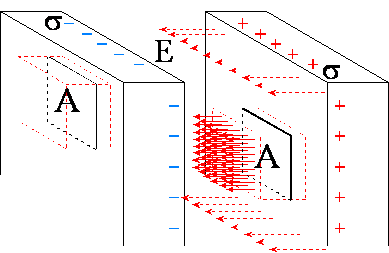
Jako powierzchnię Gaussa wybieramy prostopadłościan z jedną podstawą zanurzoną wewnątrz płyty metalowej gdzie nie ma ani ładunku ani pola E. Pole przenika tylko te podstawę prostopadłościanu, która znajduje się w przestrzeni między płytami.. Z prawa Gaussa otrzymujemy

Na zewnątrz płyt pole jest równe zeru.

Back to Index